Расстояние между прямыми в пространстве

Первый способ сводится к нахождению расстояния от точки до плоскости
Идея заключается в построении:
а) двух параллельных плоскостей, каждая из которых проходит через одну из скрещивающихся прямых, параллельно другой скрещивающейся прямой. Расстояние между этими плоскостями будет искомым.
б) в построении плоскости, проходящей через одну из скрещивающихся прямых, параллельно другой. Расстояние от любой точки второй прямой до построенной плоскости будет искомым.

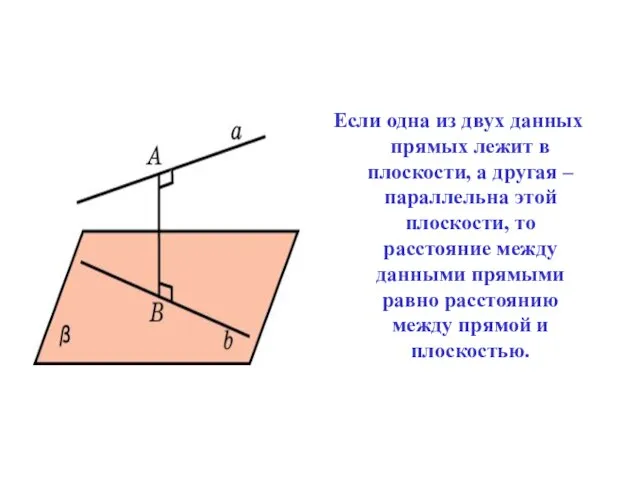
Если одна из двух данных прямых лежит в плоскости, а другая – параллельна этой плоскости, то расстояние между данными прямыми равно расстоянию между прямой и плоскостью.

Второй способ нахождения расстояния между скрещивающимися прямыми основан на методе ортогонального проектирования.
Расстояние между скрещивающимися прямыми от
точки, являющейся проекцией одной из данных
прямых на перпендикулярную ей плоскость до
проекции другой прямой на эту плоскость. Угол
между второй прямой и указанной ей проекцией
дополняет до 90° угол между данными
скрещивающимися прямыми.

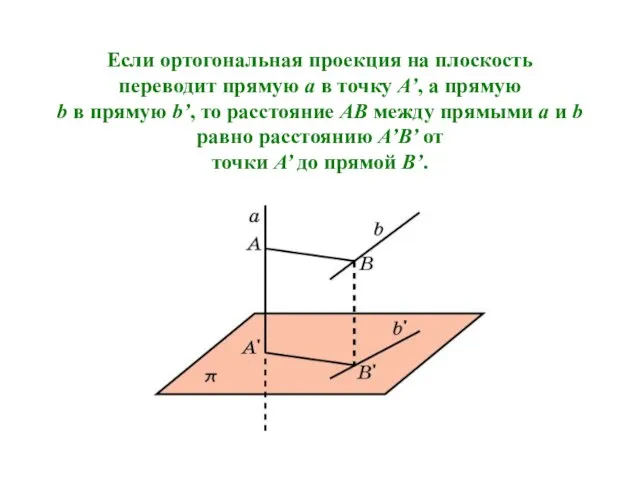
Если ортогональная проекция на плоскость переводит прямую a в точку A’, а прямую
b в прямую b’, то расстояние AB между прямыми a и b равно расстоянию A’B’ от
точки A’ до прямой B’.

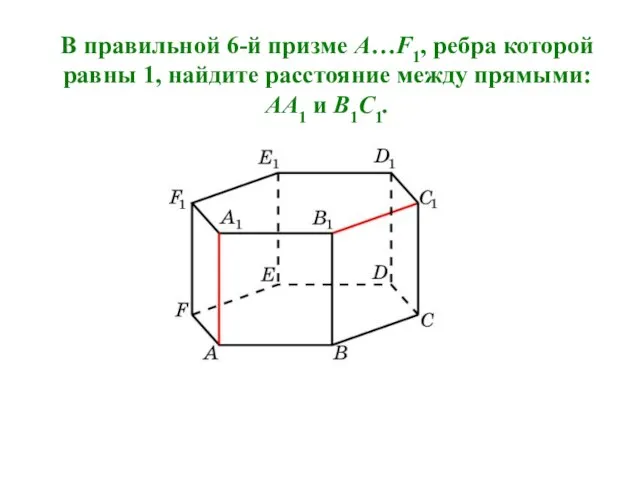
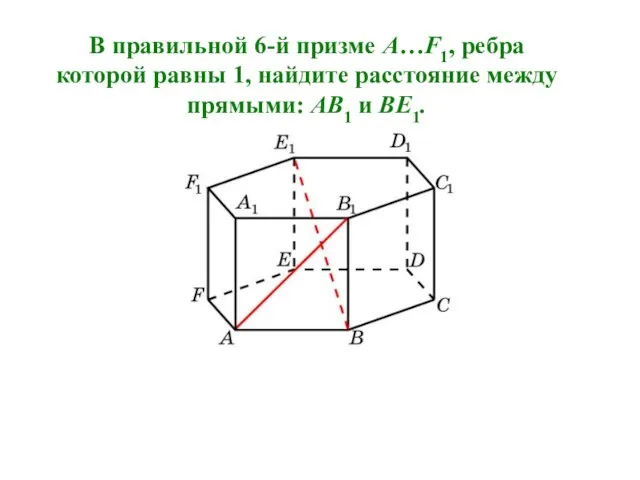
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и B1C1.

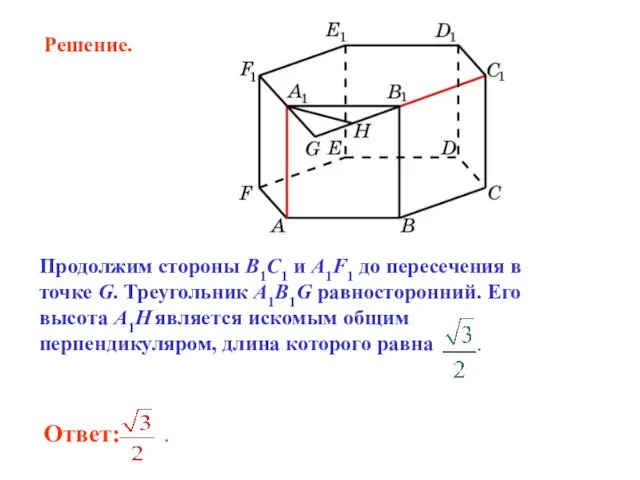
Продолжим стороны B1C1 и A1F1 до пересечения в точке G. Треугольник A1B1G равносторонний. Его высота A1H является искомым общим перпендикуляром, длина которого равна .
Решение.

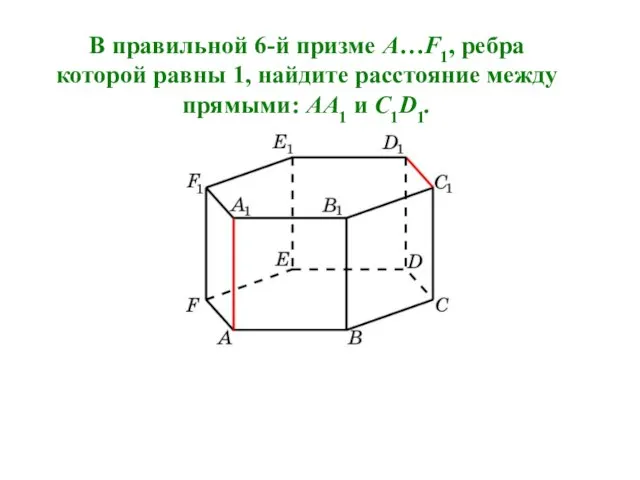
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и C1D1.

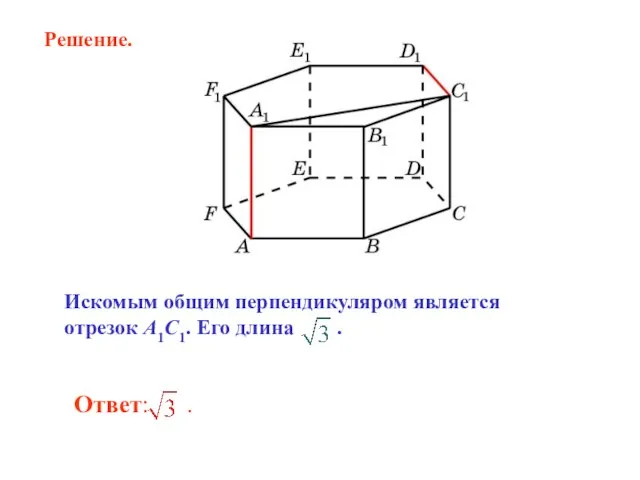
Искомым общим перпендикуляром является отрезок A1C1. Его длина .
Решение.

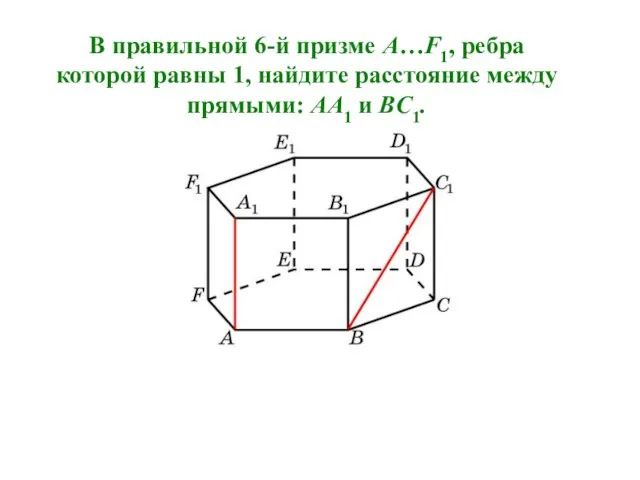
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и BC1.

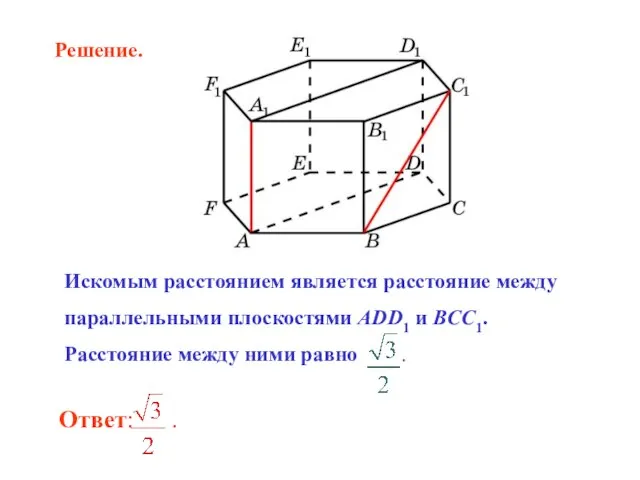
Искомым расстоянием является расстояние между
параллельными плоскостями ADD1 и BCC1.
Расстояние между ними равно .
Решение.

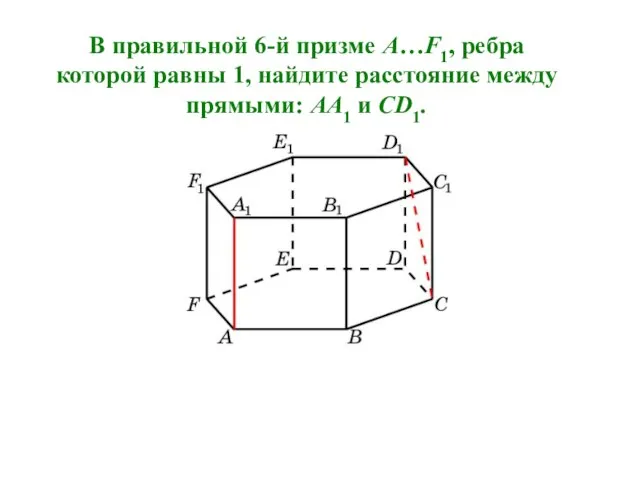
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и CD1.

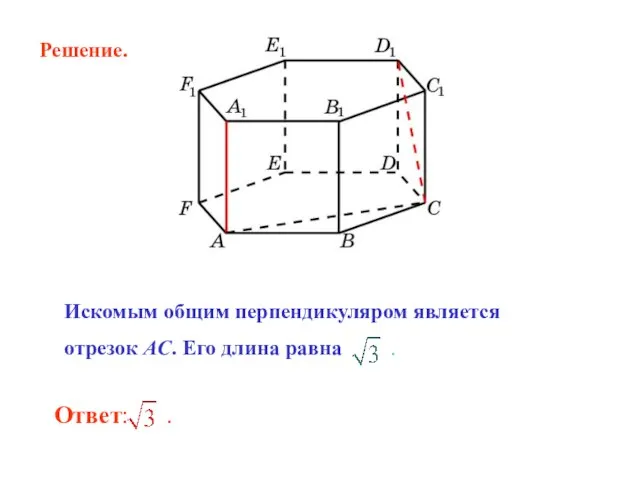
Искомым общим перпендикуляром является
отрезок AC. Его длина равна .
Решение.

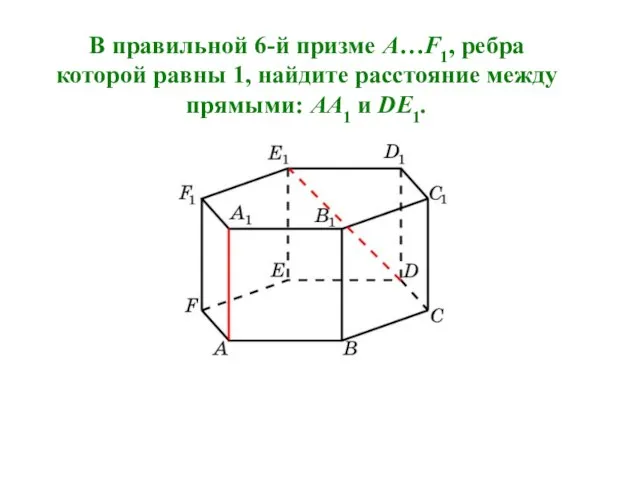
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и DE1.

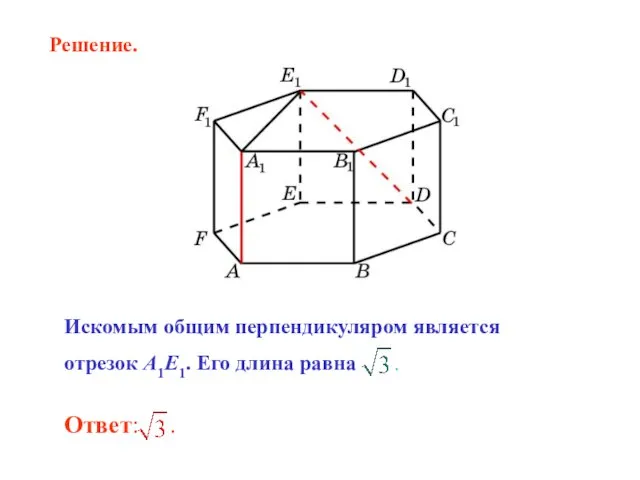
Искомым общим перпендикуляром является
отрезок A1E1. Его длина равна .
Решение.

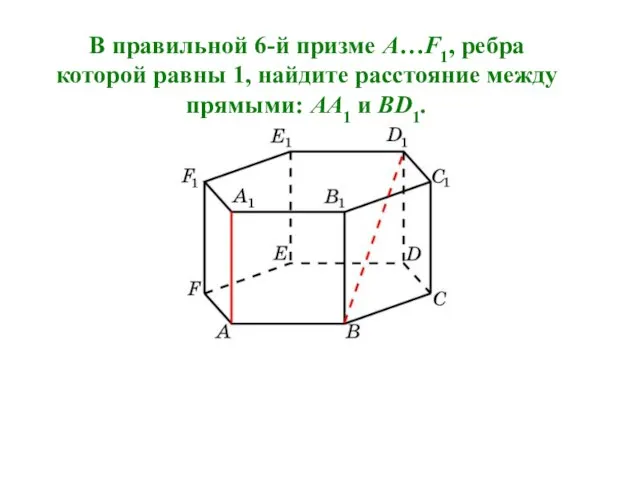
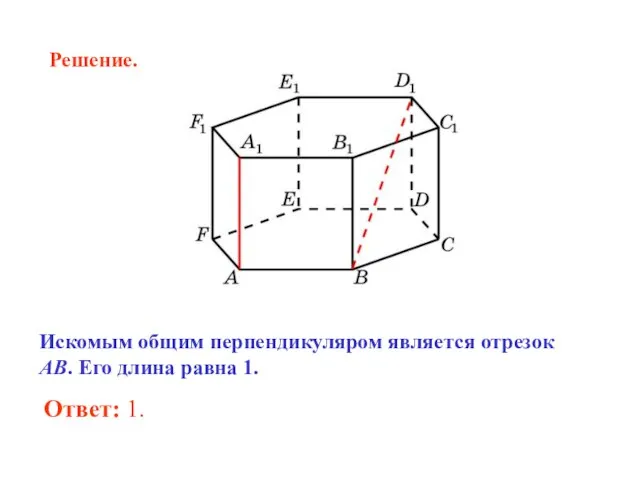
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и BD1.

Решение.

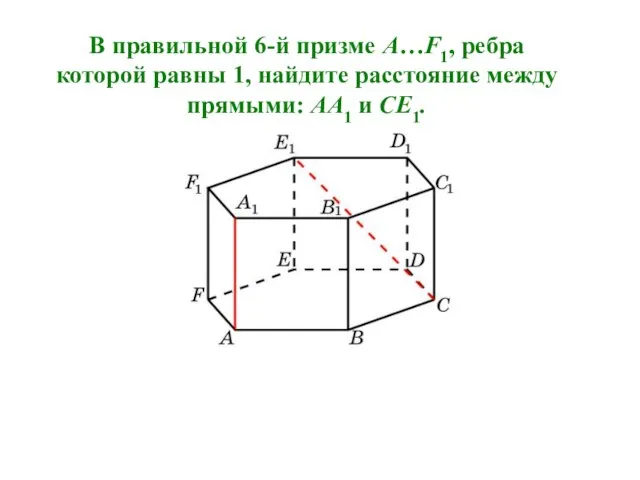
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и CE1.

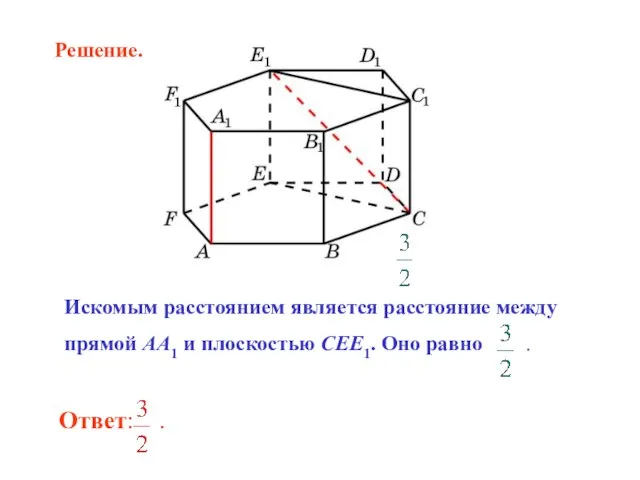
Искомым расстоянием является расстояние между
прямой AA1 и плоскостью CEE1. Оно равно .
Решение.

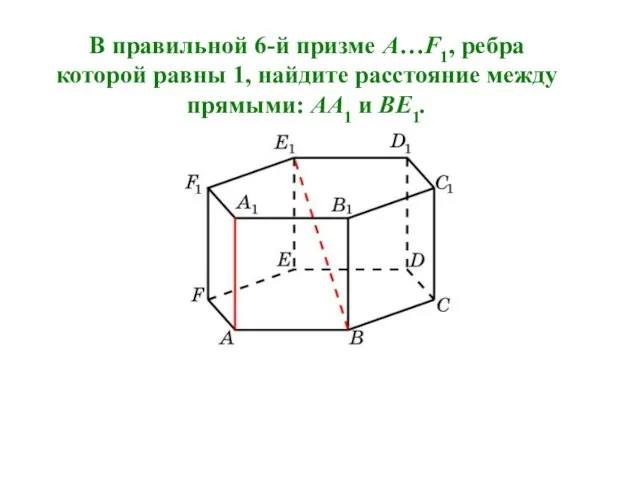
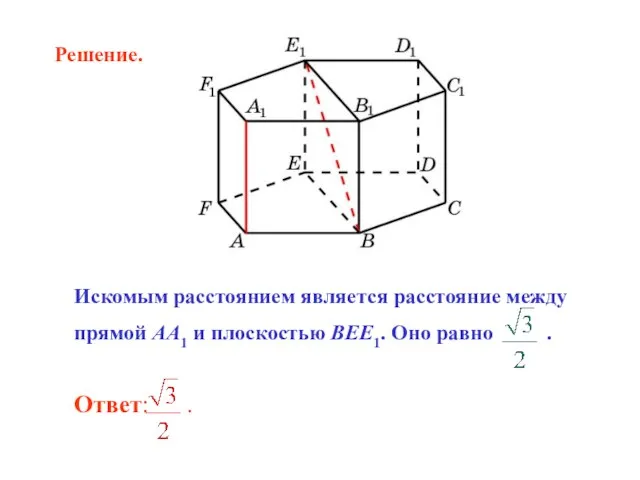
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и BE1.

Искомым расстоянием является расстояние между
прямой AA1 и плоскостью BEE1. Оно равно .
Решение.

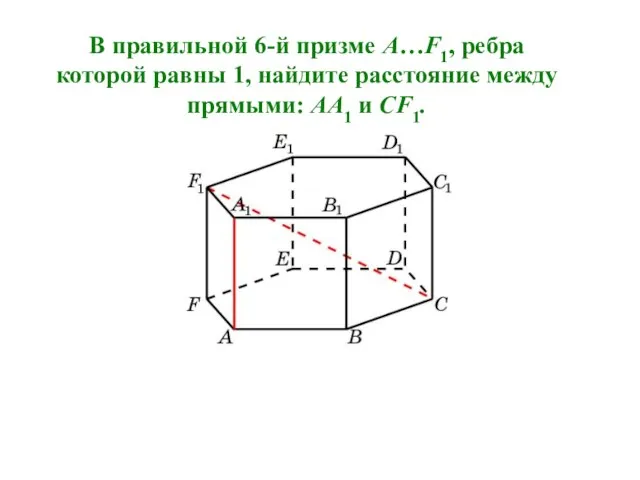
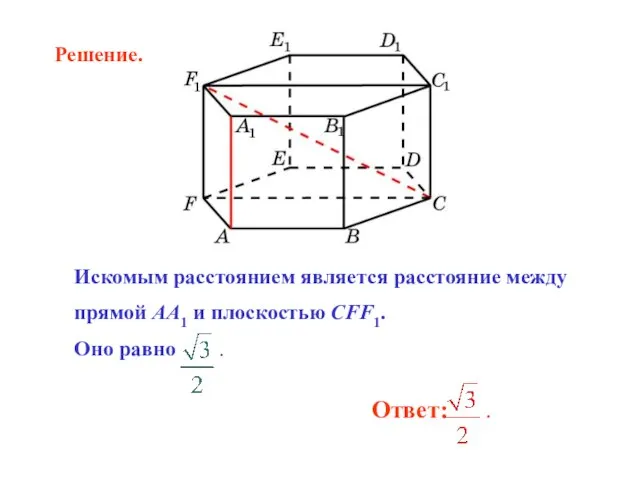
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и CF1.

Искомым расстоянием является расстояние между
прямой AA1 и плоскостью CFF1.
Оно равно .
Решение.

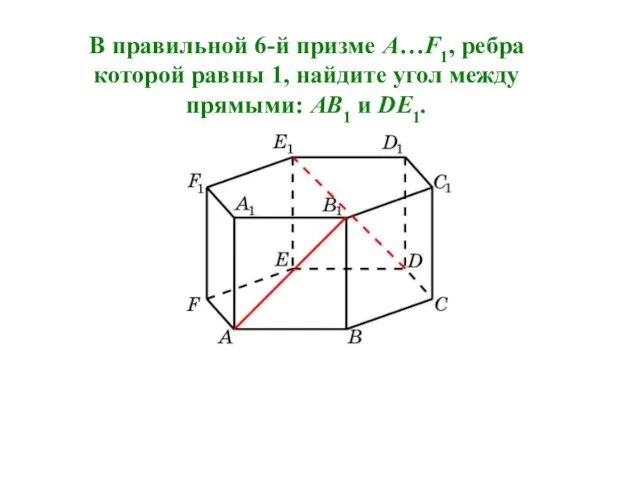
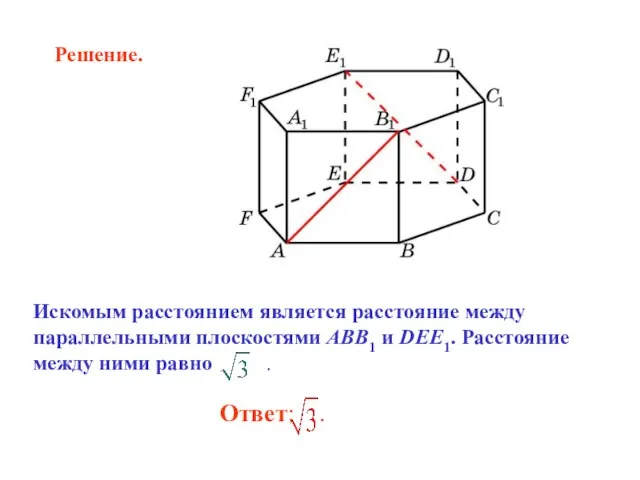
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и DE1.

Решение.

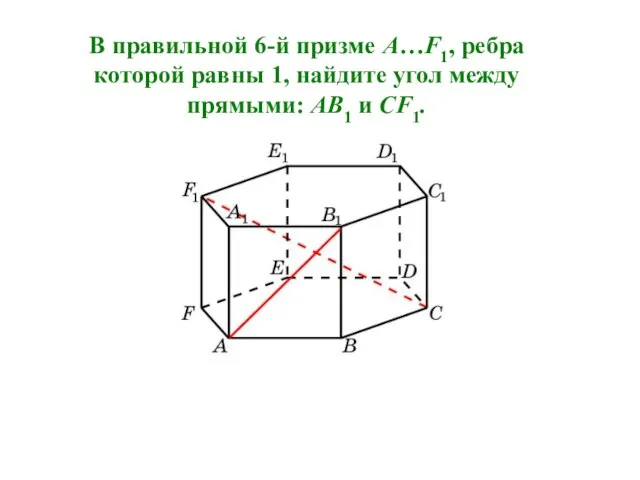
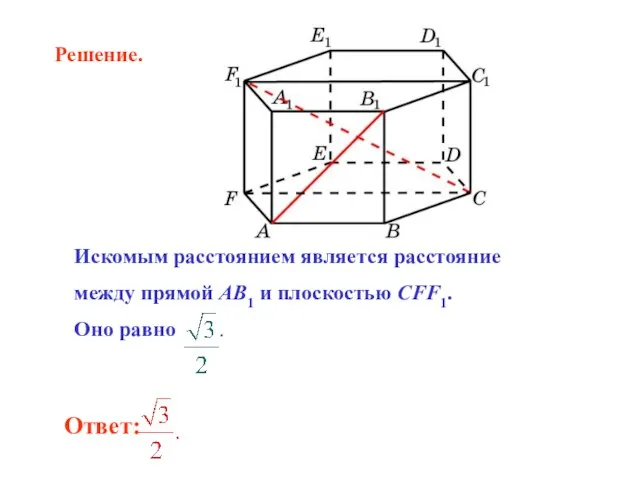
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и CF1.

Искомым расстоянием является расстояние
между прямой AB1 и плоскостью CFF1.
Оно равно .
Решение.

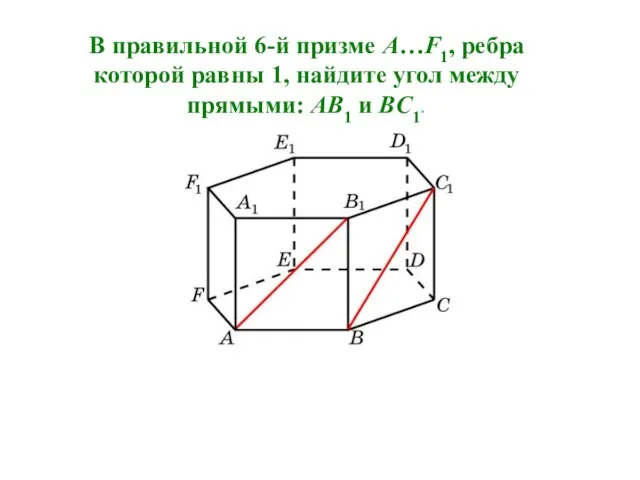
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и BC1.

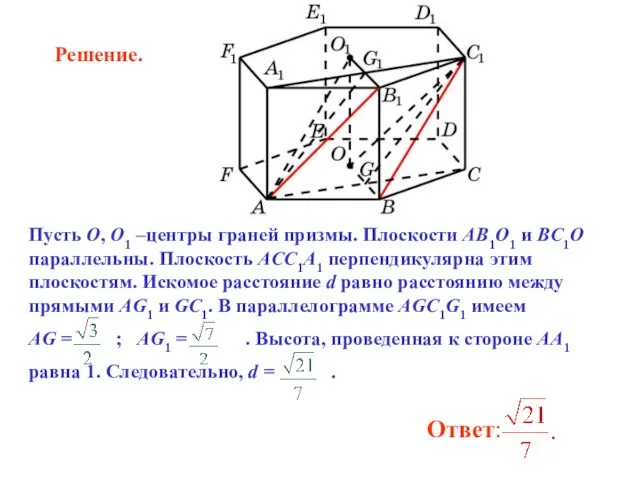
Пусть O, O1 –центры граней призмы. Плоскости AB1O1 и BC1O параллельны. Плоскость ACC1A1 перпендикулярна этим плоскостям. Искомое расстояние d равно расстоянию между прямыми AG1 и GC1. В параллелограмме AGC1G1 имеем
AG = ; AG1 = . Высота, проведенная к стороне AA1
равна 1. Следовательно, d = .
Решение.

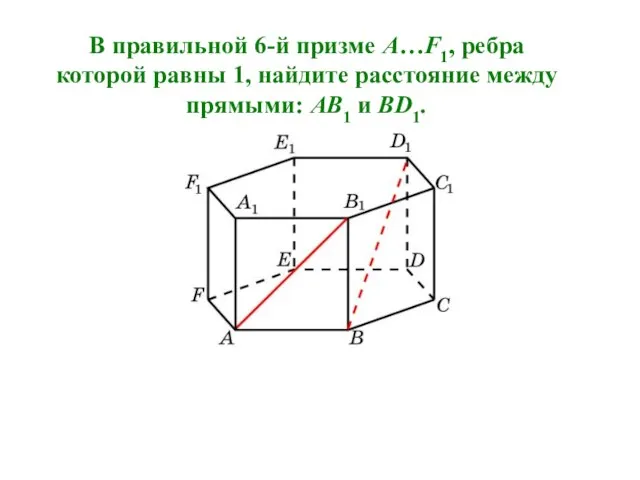
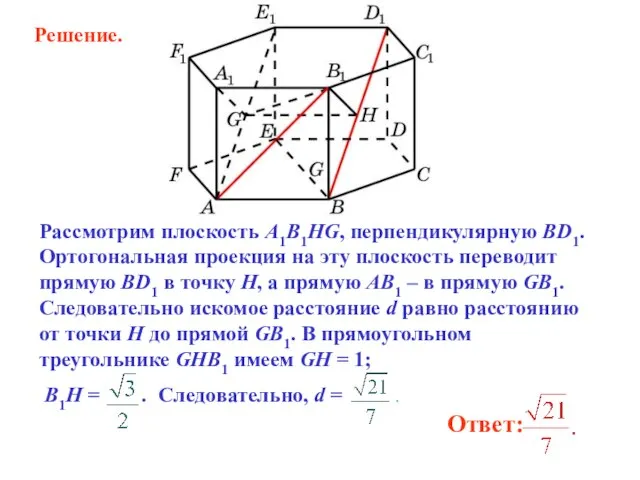
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AB1 и BD1.

Рассмотрим плоскость A1B1HG, перпендикулярную BD1. Ортогональная проекция на эту плоскость переводит прямую BD1 в точку H, а прямую AB1 – в прямую GB1. Следовательно искомое расстояние d равно расстоянию от точки H до прямой GB1. В прямоугольном треугольнике GHB1 имеем GH = 1;
B1H = . Следовательно, d = .
Решение.

В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AB1 и BE1.