Теория и алгоритмы. Решения типовых задач на взаимное пересечение геометрических объектов

Качественная сторона очерчивает круг задач, в которых определяется расположение объектов относительно друг друга
Такие задачи называют
позиционными
Красовская Н.И.

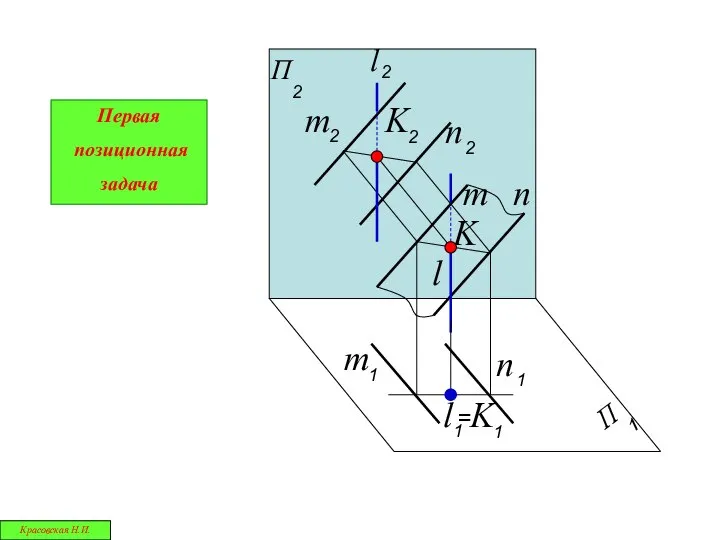
Задачу построения точек пересечения какой-нибудь заданной линии с поверхностью называют
первой основной позиционной задачей
Задачу построения линий пересечения
двух заданных поверхностей называют
второй основной позиционной задачей
Красовская Н.И.

Решение задач на пересечение геометрических
объектов, занимающих
проецирующее положение
Красовская Н.И.

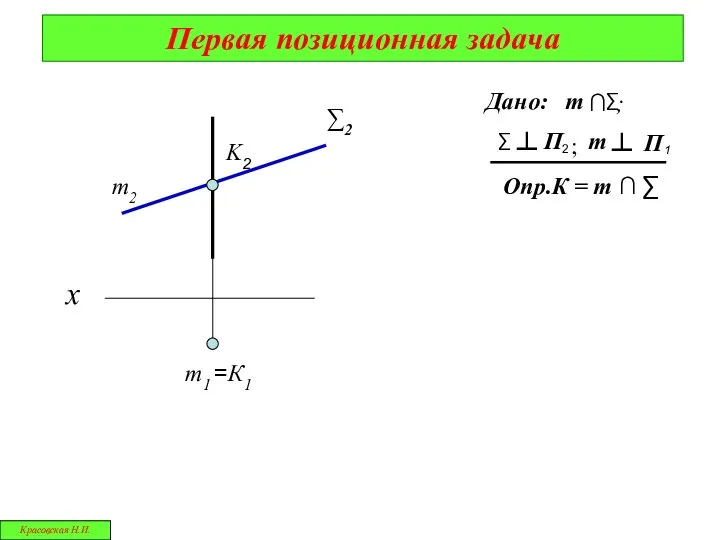
Первая позиционная задача
х
∑2
m2
=К1
Дано:
;
Опр.К = m ∩ ∑
K2
m1
Красовская Н.И.

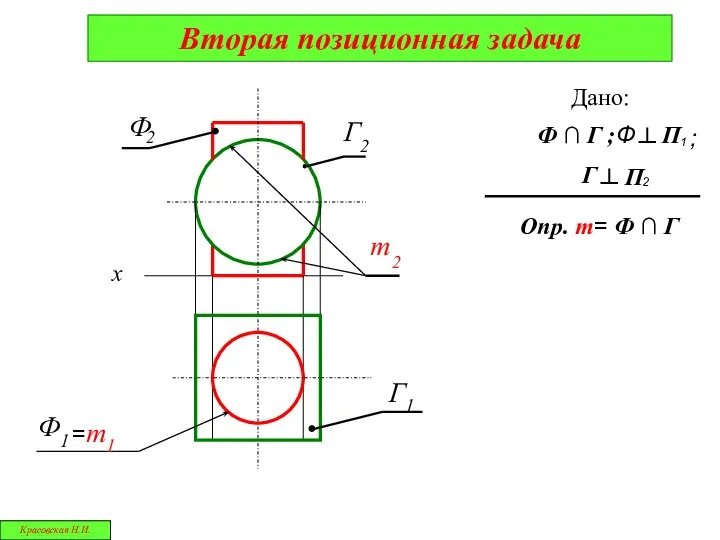
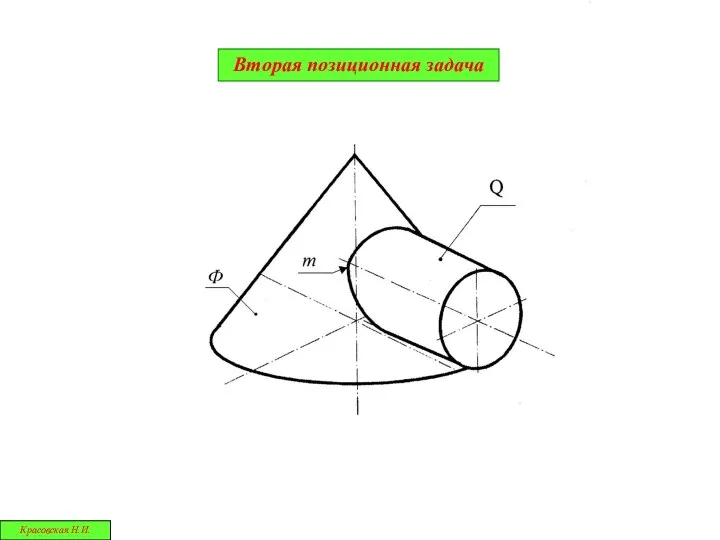
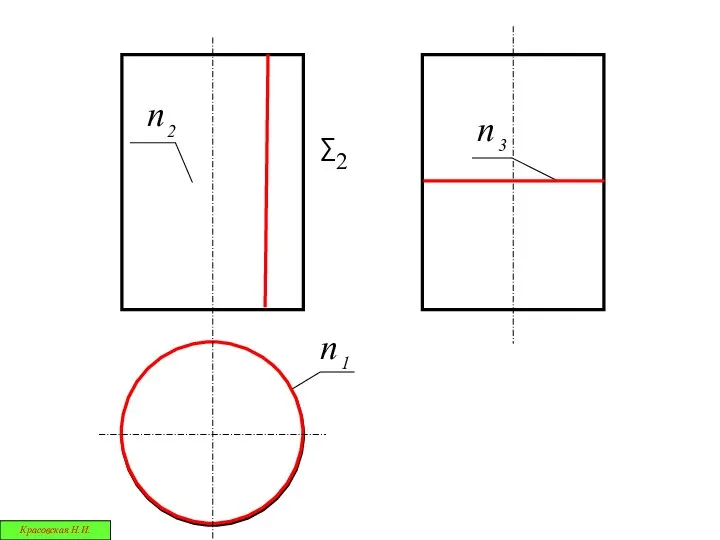
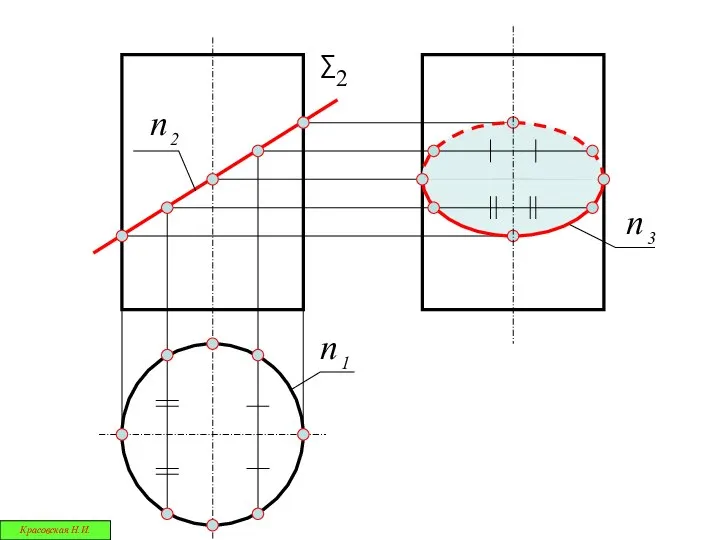
Ф1
Г1
Дано:
Ф ∩ Г ;
Опр. m= Ф ∩ Г
Вторая позиционная задача
х
Г2
=m1
Красовская Н.И.

Искомый общий элемент
уже задан
на чертеже
2. Его проекции частично или полностью
совпадают с заданными проекциями-носителями пересекающихся проецирующих геометрических объектов
3. Решение задачи
сводится к обозначению
проекций искомого общего элемента
4. Третья проекция элемента пересечения находится
по законам проекционной связи
Aлгоритм
Красовская Н.И.

Решение задач
на пересечение проецирующего геометрического объекта с геометрическим объектом
общего положения
Красовская Н.И.

=
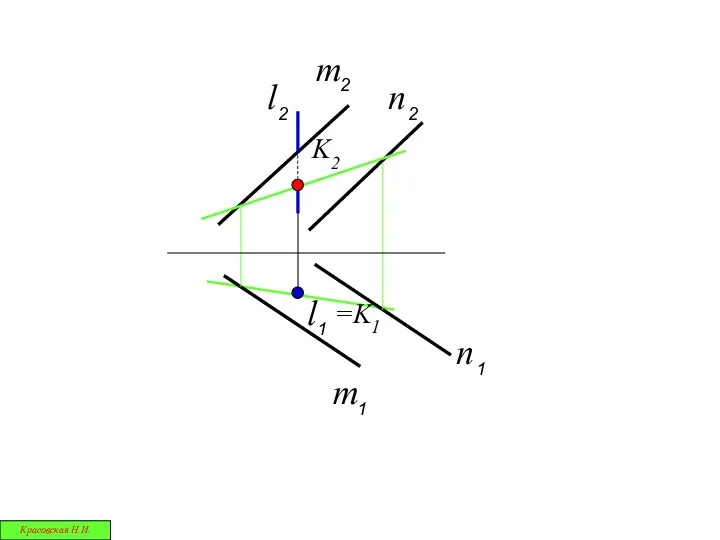
Первая
позиционная
задача
Красовская Н.И.

=K1
K2
Красовская Н.И.

Красовская Н.И.

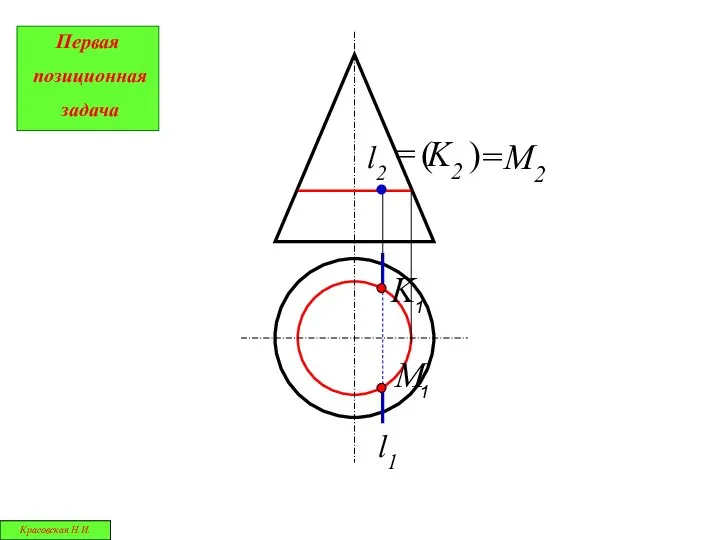
l1
l2
( )
= K2
=M2
Первая
позиционная
задача
Красовская Н.И.

Красовская Н.И.

Красовская Н.И.

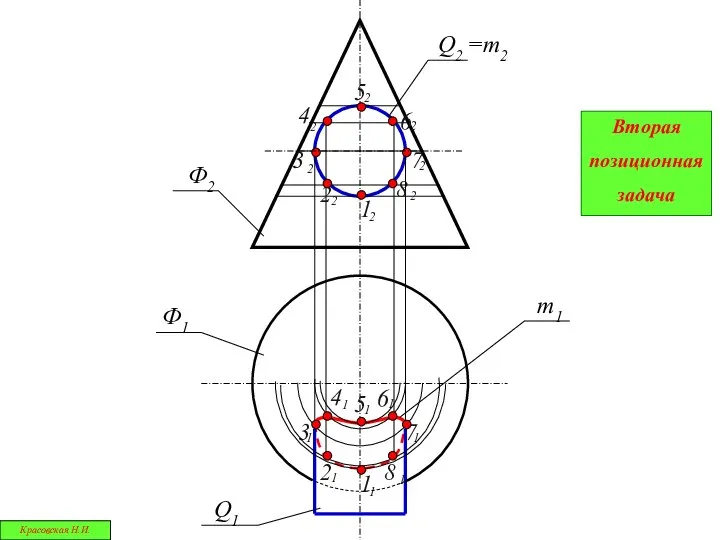
Вторая позиционная задача
Красовская Н.И.

Красовская Н.И.

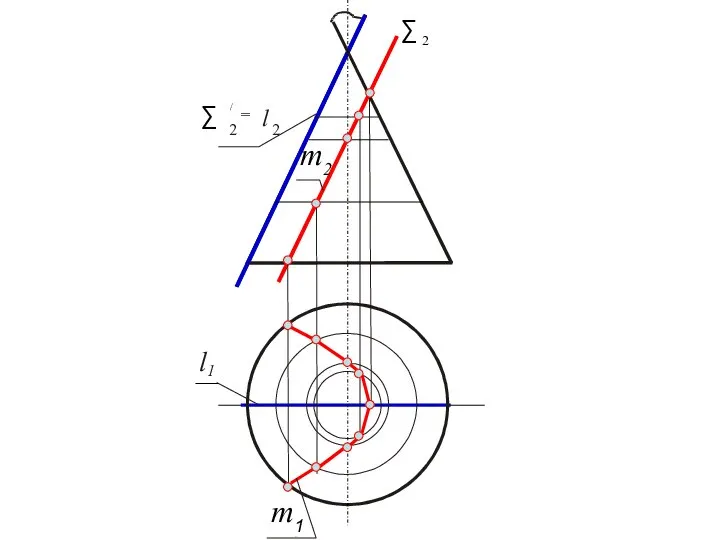
=m2
m1
Q2
Вторая
позиционная
задача
Красовская Н.И.

1.Одна проекция искомого общего элемента уже задана на чертеже
4. Третья проекция элемента пересечения строится
по законам проекционной связи
3. Вторая проекция искомого общего элемента находится
из условия принадлежности геометрическому объекту общего положения
2. Она частично или полностью
совпадает с заданной проекцией — носителем проецирующего геометрического объекта
Алгоритм
Красовская Н.И.

Сечение поверхностей проецирующей плоскостью
Красовская Н.И.

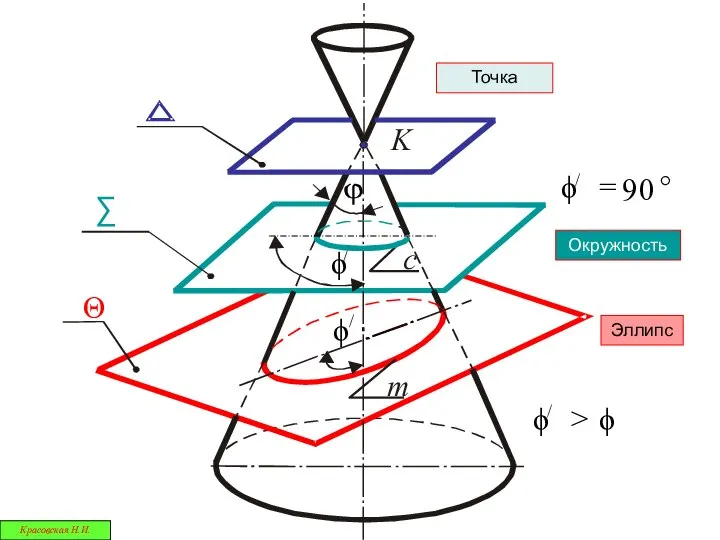
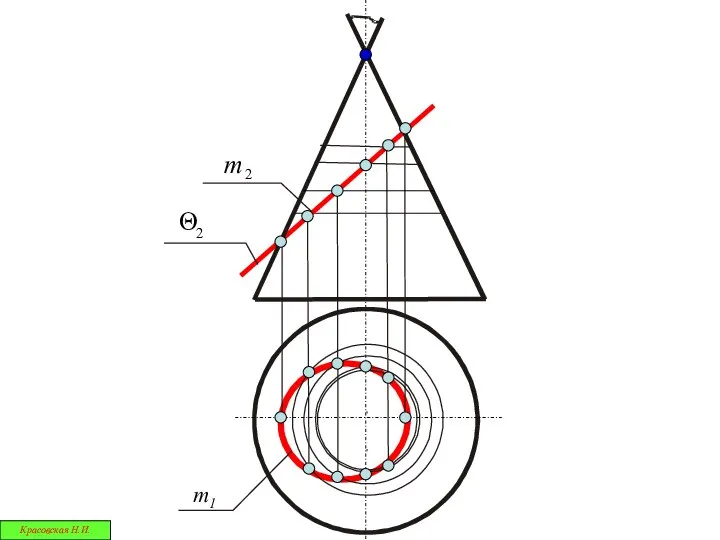
Конические
сечения
Красовская Н.И.

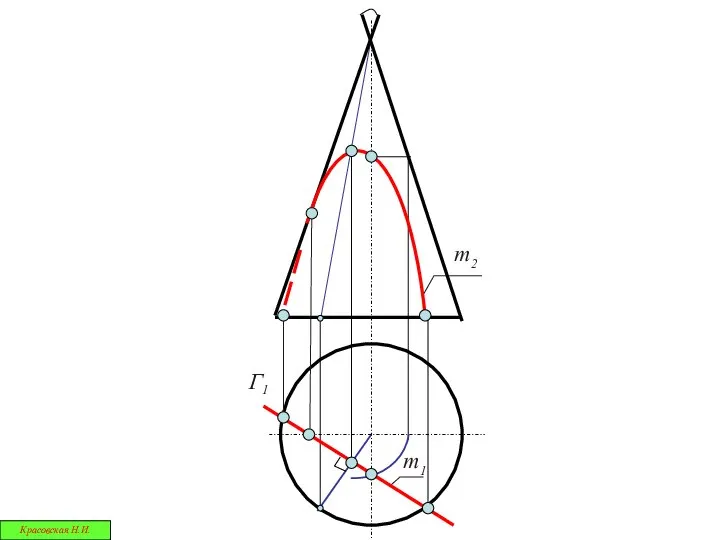
В результате сечения конической поверхности плоскостью получаются кривые второго порядка:
окружности, эллипсы, параболы и гиперболы
Эти кривые называют
кониками
Красовская Н.И.

/
K
Точка
Окружность
Эллипс
Красовская Н.И.

Красовская Н.И.

Красовская Н.И.

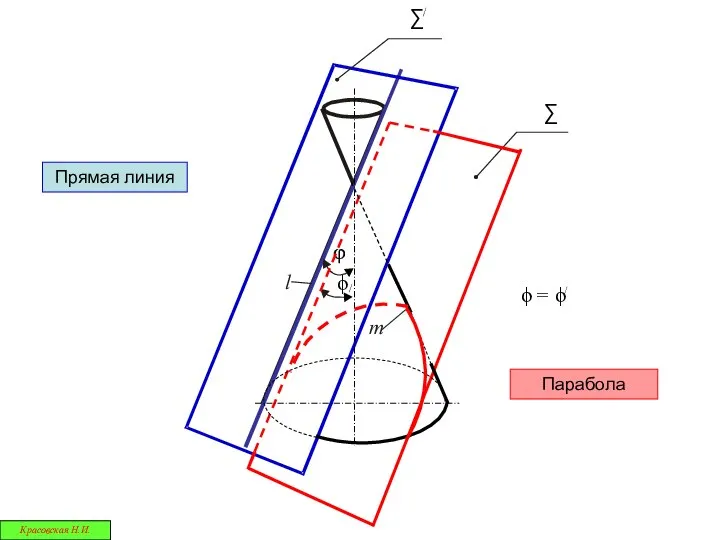
Прямая линия
Парабола
Красовская Н.И.

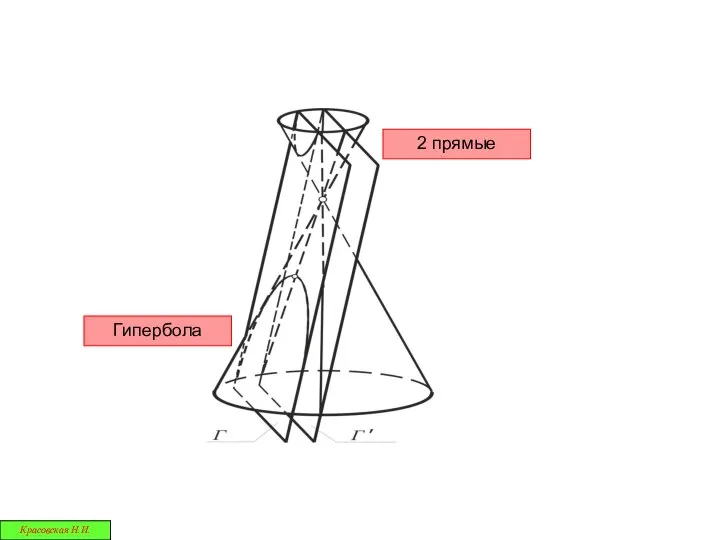
2 прямые
Гипербола
Красовская Н.И.

Красовская Н.И.

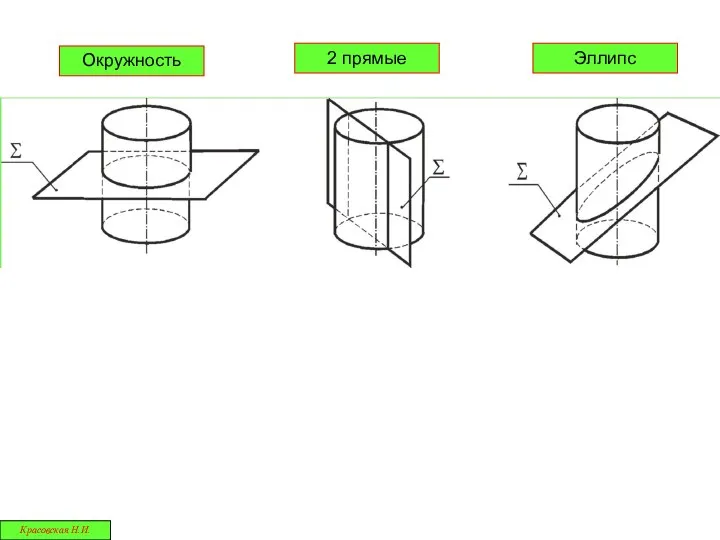
Цилиндрические сечения
Красовская Н.И.

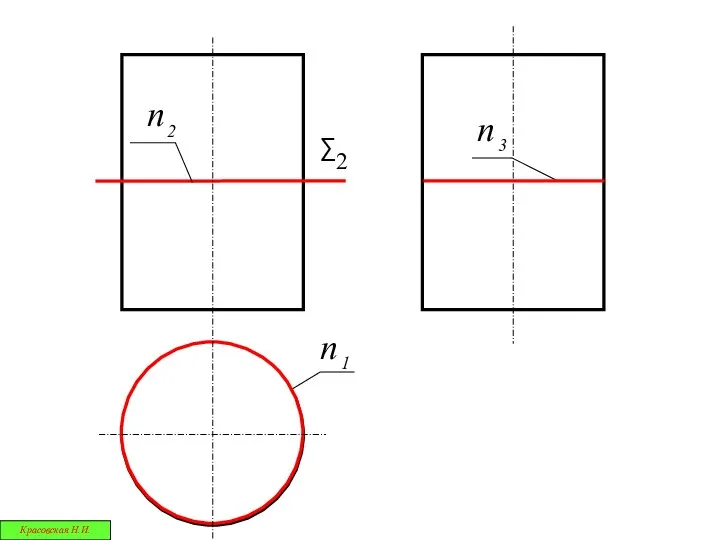
Окружность
Эллипс
2 прямые
Красовская Н.И.

Красовская Н.И.

Красовская Н.И.

Красовская Н.И.

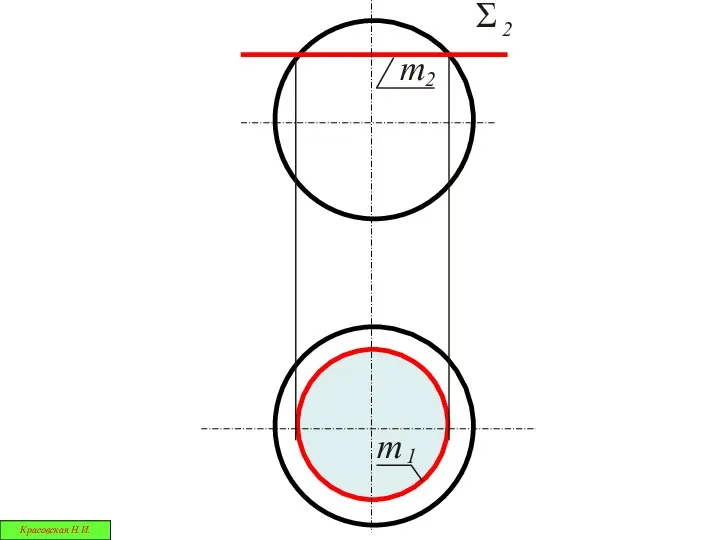
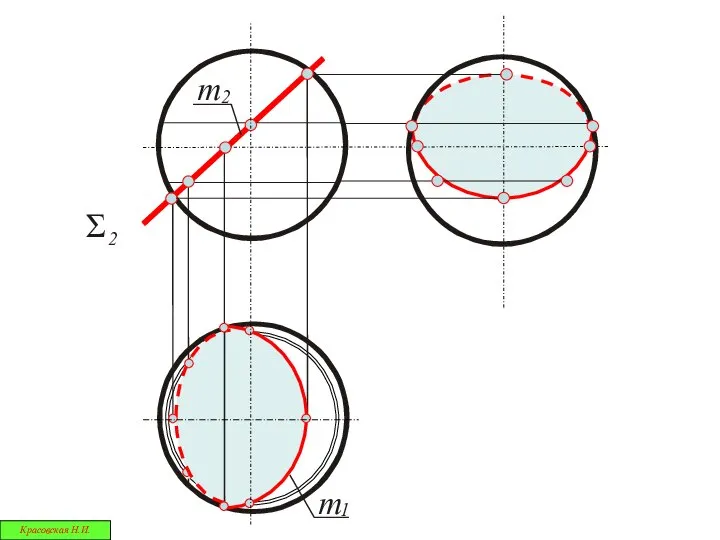
Сферические
сечения
Красовская Н.И.

При пересечении поверхности сферы плоскостью всегда получается
окружность
Красовская Н.И.

Красовская Н.И.

Красовская Н.И.

Красовская Н.И.

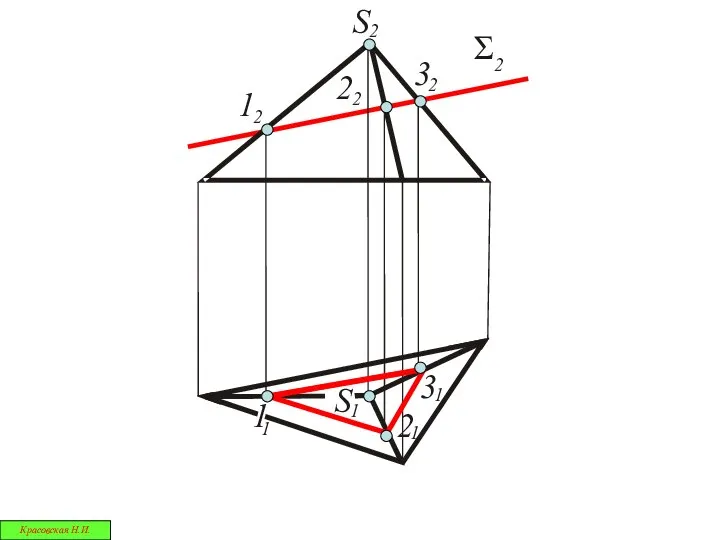
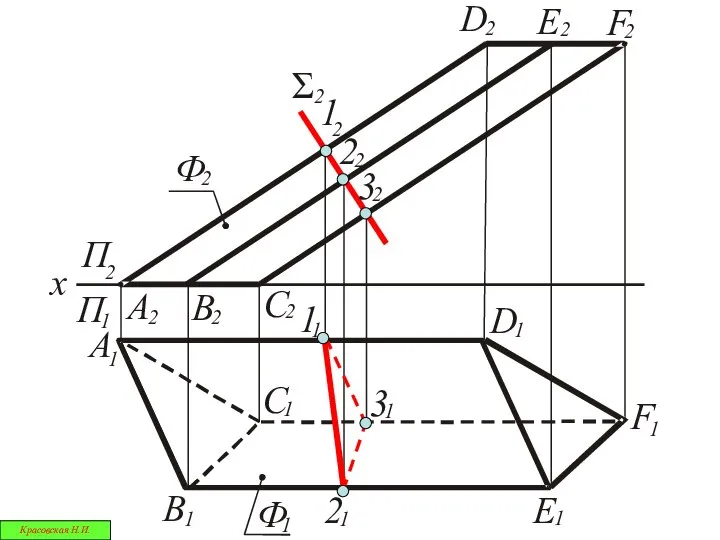
Сечения многогранника проецирующей плоскостью
Красовская Н.И.

В сечении многогранной поверхности всегда получается плоский многоугольник
Красовская Н.И.

S
S
1
2
Красовская Н.И.

Ф
2
D
F
E
2
2
2
A
A
B
C
C
1
1
1
1
1
D
F
E
2
2
2
П
2
П
1
x
Красовская Н.И.