Раздел II. Взаимодействие e- и e+ с веществом.

Раздел II.
1. Ионизационные потери.
Механизм ионизационных потерь e± в веществе схож со случаем тяжелых заряженных частиц. Поэтому вывод формулы для ионизационных потерь аналогичен выводу формулы Бете-Блоха. Однако есть принципиальные отличия, которые заключаются в учете обменных эффектов, когда речь идет о прохождении e- через вещество. Правда, роль обменных эффектов становится заметной только для достаточно медленных электронов.

Кинематика рассеяния
Частица с массой M, энергией E и импульсом p
сталкивается с покоящейся частицей с массой m.
Законы сохранения энергии и импульса:
Решение системы уравнений:

Особенности кинематики
Максимальное значение передаваемой энергии T достигается при θ0=0
(лобовое столкновение):
Отсюда, поскольку M=m=me, имеем
В нерелятивистском пределе (γ → 1):
В ультрарелятивистском пределе (γ → ∞, β → 1):

Обменные эффекты
Пусть быстрый электрон с энергией Te рассеивается на угол θ в результате столкновения с покоящимся электроном вещества. В нерелятивистском случае сечение дается следующей формулой Мотта:
«прямой»
процесс
«обменный»
процесс
интерференция «прямого»
и «обменного» процессов
Учитывая, что передаваемая энергия есть T = Te⋅sin2θ, имеем

Удельные потери энергии
Нерелятивистский предел (γ → 1):
Ультрарелятивистский предел (γ → ∞, β → 1):

(1) При одинаковой кинетической энергии электронов и тяжелых заряженных частиц в нерелятивистском случае удельные потери энергии пропорциональны массе частиц (в силу закона ~ 1/υ2). Например, для протонов потери в 2000 раз больше, чем для электронов.
(2) В ультрарелятивистском случае эта разница нивелируется. Например, при кинетических энергиях электрона и протона, равных 10 ГэВ, удельные потери энергии электрона в 2 раза превышают удельные потери энергии протона.

Раздел II.
2. Тормозное излучение.
Наряду с ионизационными потерями важную роль в прохождении e± через вещество, в отличие от случая тяжелых заряженных частиц, играют радиационные потери энергии на тормозное излучение («Bremsstrahlung»; от немецких слов «Bremsen» - торможение и «Strahlung» - излучение). Тормозное излучение возникает в результате взаимодействия e± с кулоновским полем ядер и электронов вещества.

Общие замечания
Согласно классической электродинамике интенсивность излучения, испускаемого заряженной частицей с массой m, которая движется с ускорением a, есть W ~ a2 = (F/m)2, где F – сила, действующая на частицу. Со стороны ядра с зарядом Z на частицу действует кулоновская сила F ~ Z. Отсюда W ~ (Z/m)2. Таким образом, можно сделать следующие качественные выводы:
(1) Потери энергии на излучение обратно пропорциональны квадрату массы частицы, т.е. чем легче заряженная частица, тем интенсивнее она излучает. Например, излучение электрона в 40 000 раз интенсивнее излучения мюона и в 4 000 000 раз интенсивнее излучения протона! Поэтому радиационные потери энергии имеют наибольшее значение для легчайших заряженных частиц – электронов и позитронов.
(2) Излучаемая энергия прямо пропорциональны квадрату заряда вещества, т.е. радиационные потери наиболее существенны в тяжелых веществах (например, в свинце).

Теория Бете-Гайтлера
Вальтер Гайтлер
(Walter Heitler, 1904 - 1981)
Ханс Бете
(Hans Bethe, 1906 - 2005)
В 1934 году Бете и Гайтлер впервые описали тормозное излучение электрона в кулоновском поле ядра в рамках квантовой электродинамики:
(1) электрон описывался с помощью свободного уравнения Дирака;
(2) взаимодействие электрона с ядром учитывалось в борновском приближении.

Формула Бете-Гайтлера
Бете и Гайтлер получили следующую формулу для дифференциального сечения dσω излучения тормозного фотона с частотой ω в интервал частот (ω,ω+dω) релятивистским электроном с энергией E:
Функции Φ1 и Φ2 учитывают экранирование кулоновского поля ядра атомными электронами. Очевидно, что эти функции зависят от расстояния Lc (так называемая длина когерентности), которое проходит виртуальный фотон, и энергии электрона E.

Экранировка
Когда Lc ≥ a, где a = a0⋅Z-1/3 – радиус атома в модели Томаса-Ферми, становятся важными эффекты экранирования заряда ядра электронами атома. Для оценок воспользуемся соотношением неопределенности для виртуального фотона Lc⋅q ≥ ћ.
Таким образом, для малых энергий тормозного фотона ħω = E-E′ всегда имеем Lc > a, т.е. наступает полное экранирование. Если же тормозной фотон жесткий, причем ħω ~ E′, то полное экранирование наступает при E > 137⋅Z-1/3mec2.

Если E << 137⋅Z-1/3mec2, то экранирование несущественно:
Если E >> 137⋅Z-1/3mec2, то реализуется режим полного экранирования:

Спектр тормозных фотонов
Рис. Спектры тормозного излучения для платиновой мишени при различных полных энергиях электрона Е0.
Как следует из формулы Бете-Гайтлера, спектр тормозных фотонов, т.е. распределение излученных фотонов по энергиям, имеет следующие свойства:
(1) спектр является сплошным;
(2) при малых энергиях тормозных γ-квантов Eγ = ħω спектр имеет вид гиперболы ~ 1/Eγ;
(3) верхняя граница спектра определяется кинетической энергией электрона
Te = E - mec2.

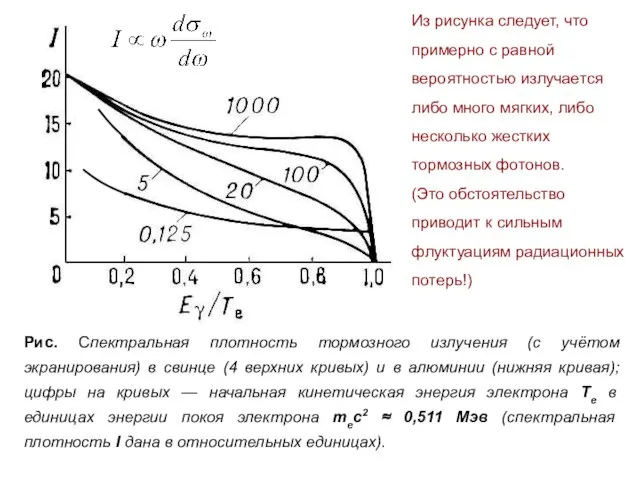
Рис. Спектральная плотность тормозного излучения (с учётом экранирования) в свинце (4 верхних кривых) и в алюминии (нижняя кривая); цифры на кривых — начальная кинетическая энергия электрона Te в единицах энергии покоя электрона mec2 ≈ 0,511 Мэв (спектральная плотность I дана в относительных единицах).
Из рисунка следует, что примерно с равной вероятностью излучается либо много мягких, либо несколько жестких тормозных фотонов.
(Это обстоятельство приводит к сильным флуктуациям радиационных потерь!)

Угловое распределение
В общем случае угловое распределение тормозного излучения имеет сложный характер. Оно становится простым в предельном случае малых и больших энергий электрона. В нерелятивистском случае сечение тормозного излучения dσ можно представить в виде произведения сечения упругого резерфордовского рассеяния электрона dσs и вероятности излучения фотона dwγ:
Таким образом, интенсивность излучения достигает максимума в направлении, перпендикулярном к плоскости движения электрона (p,p′).

Рис. Угловое распределение интенсивности тормозного излучения в ультрарелятивистском случае (Te >> mec2).
Чем выше энергия электронов E, тем больше фотонов будет излучаться по направлению движения электронов. В ультрарелятивистском случае
(E >> mec2) фотоны сильно коллимированы в направлении движения электронов. Угловое распределение фотонов имеет следующий вид:
Отсюда следует, что средний угол вылета фотонов равен <θ> = mec2/E . Таким образом, чем выше энергия электронов E, тем острее конус тормозного излучения.

Удельные потери энергии
Среднюю потерю энергии на тормозное излучение на единице длины пути электрона в веществе можно определить как
В нерелятивистском случае (Te << mec2) интегрирование дает
В ультрарелятивистском случае (Te >> mec2), учитывая что в этом случае сечение ТИ на электроне отличается от сечения на ядре только фактором Z2:

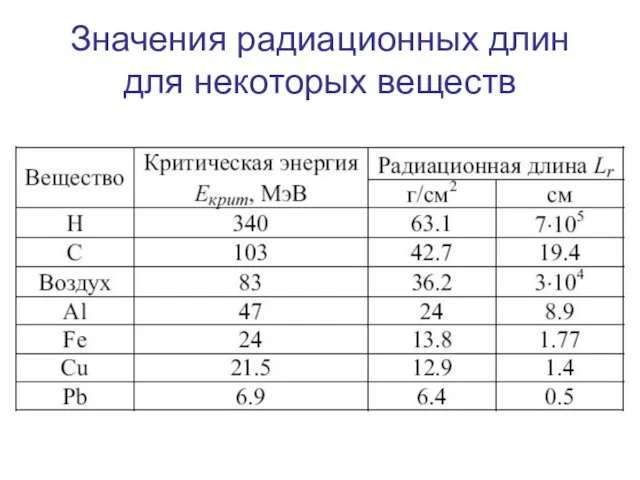
Радиационная длина
Итак, при очень высоких энергиях электронов удельные радиационные потери энергии можно представить в виде:
где Lr – так называемая радиационная длина.
Получим закон убывания энергии электрона за счет тормозного излучения:
Таким образом, при прохождении электроном слоя вещества толщиной Lr его энергия в среднем за счет тормозного излучения уменьшается в e раз.

Значения радиационных длин для некоторых веществ

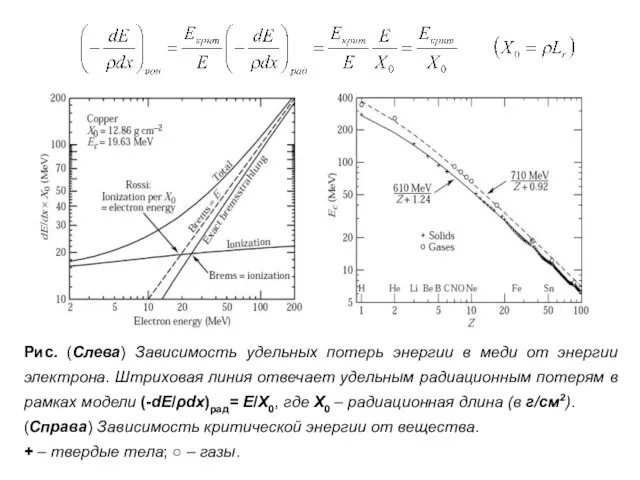
Критическая энергия
Сравним удельные потери энергии ультрарелятивистского электрона на тормозное излучение и ионизацию:
где мы пренебрегли логарифмической зависимостью ионизационных потерь от энергии электрона.
Энергия электрона Eкрит, при которой потери на излучение становятся равными потерям на ионизацию, называется критической энергией:

Рис. (Слева) Зависимость удельных потерь энергии в меди от энергии электрона. Штриховая линия отвечает удельным радиационным потерям в рамках модели (-dE/ρdx)рад= E/X0, где X0 – радиационная длина (в г/см2).
(Справа) Зависимость критической энергии от вещества.
+ – твердые тела; ○ – газы.

Раздел II.
3. ЛПМ-эффект.
Тормозное излучение релятивистского электрона (также как рождение пары γ-квантом высокой энергии) формируется в большой пространственной области вдоль импульса частицы. Эта область носит название зоны формирования излучения или длины когерентности Lc. При достаточно высоких энергиях электронов Lc может достигать макроскопических размеров и даже превышать размер самой мишени! Ландау и Померанчук показали [1], что многократное рассеяние релятивистского электрона на атомах среды в пределах длины когерентности процесса тормозного излучения может привести к значительному уменьшению спектральной плотности излучения по сравнению с результатом теории Бете и Гайтлера. Количественная теория этого явления, получившего название эффекта Ландау-Померанчука-Мигдала (ЛПМ-эффекта), была развита Мигдалом на основе метода кинетического уравнения [2]. При высоких энергиях ЛПМ-эффект приводит к существенному подавлению излучения и должен учитываться при проектировании детекторов и защиты для ускорителей сверхвысоких энергий.
[1] Ландау Л.Д., Померанчук И.Я., ДАН СССР. 92 (1953) 535, 735 ;
[2] Мигдал А.Б., ДАН СССР 96 (1954) 49.

Механизм ЛПМ-эфекта
В процессе испускания тормозного γ-кванта электрон обменивается виртуальным фотоном с ядром. Если электрон ультрарелятивистский
(Ee/m = γ >> 1), а тормозной γ-квант «мягкий» (Eγ << Ee), то «продольная» составляющая импульса фотона есть (см. пункт 2, Экранировка)
Согласно соотношению неопределенности виртуальный фотон проходит расстояние Lc ~ 1/q||, (Lc - длина когерентности). Нетрудно видеть, что при достаточно больших энергиях электрона длина когерентности становится вполне макроскопической величиной даже не для очень «мягких» γ-квантов. На этой длине электрон может испытать многократное кулоновское рассеяние. Если средний угол такого рассеяния <θ> ~ Zα(nLc)½/Ee сравним или превышает средний угол вылета тормозного γ-кванта <θT> = 1/γ, то тормозное излучение подавляется (ЛПМ-эффект). Таким образом, в спектре тормозного излучения должно наблюдаться подавление в области низких энергий по сравнению с теорией Бете-Гайтлера.

Из условия <θ> = <θT> можно определить частоту тормозных фотонов ωLPM, при которой возникает ЛПМ-эффект:
Таким образом, при фотонных частотах ω ≤ ωLPM происходит подавление интенсивности тормозного излучения за счет ЛПМ-эффекта.
Спектральная плотность излучения I(ω) в области ω ≤ ωLPM описывается формулой Мигдала, согласно которой
ЛПМ
Бете-Гайтлер

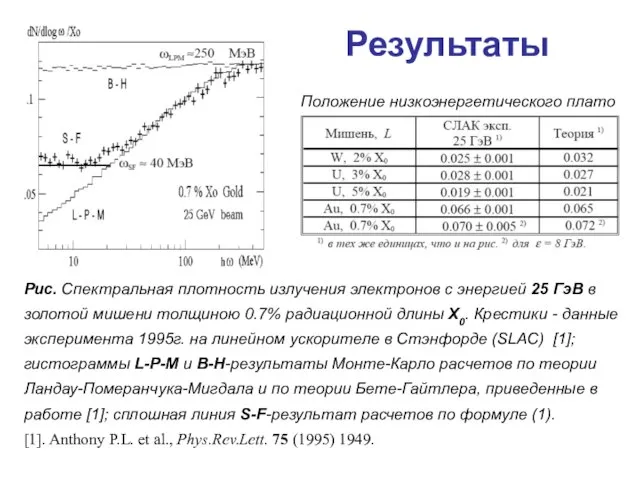
Теория в случае L < Lc

Рис. Спектральная плотность излучения электронов с энергией 25 ГэВ в золотой мишени толщиною 0.7% радиационной длины X0. Крестики - данные эксперимента 1995г. на линейном ускорителе в Стэнфорде (SLAC) [1]; гистограммы L-P-M и B-H-результаты Монте-Карло расчетов по теории Ландау-Померанчука-Мигдала и по теории Бете-Гайтлера, приведенные в работе [1]; сплошная линия S-F-результат расчетов по формуле (1).
[1]. Anthony P.L. et al., Phys.Rev.Lett. 75 (1995) 1949.
Результаты
Положение низкоэнергетического плато

Раздел II.
4. Пробеги e± в веществе.
Характер движения электронов через вещество существенно иной, чем в случае тяжелых заряженных частиц. Траектория электронов прямолинейна только в начале пути. Среднеквадратичный угол многократного рассеяния нарастает как <θ2>1/2 ~ x1/2. После большого числа актов рассеяния уже нельзя говорить о преимущественном направлении скоростей электронов – наступает режим диффузии. Наконец, в результате потерь энергии происходит полная остановка.

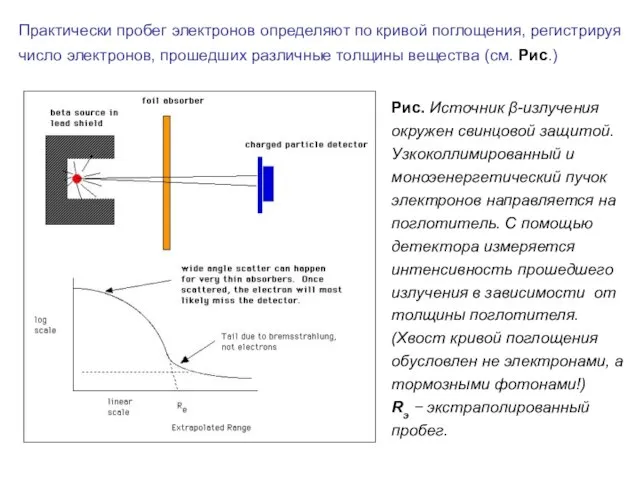
Практически пробег электронов определяют по кривой поглощения, регистрируя число электронов, прошедших различные толщины вещества (см. Рис.)
Рис. Источник β-излучения окружен свинцовой защитой. Узкоколлимированный и моноэенергетический пучок электронов направляется на поглотитель. С помощью детектора измеряется интенсивность прошедшего излучения в зависимости от толщины поглотителя.
(Хвост кривой поглощения обусловлен не электронами, а тормозными фотонами!)
Rэ − экстраполированный пробег.

Оценка R
Оценить полный пробег R или, иными словами, толщину мишени, при которой электрон теряет всю свою энергию E0, можно следующим образом (в массовых единицах длины):
X0 и Eкрит – радиационная длина и критическая энергия для вещества мишени.
Если E0 << Eкрит , то имеем приближенно:

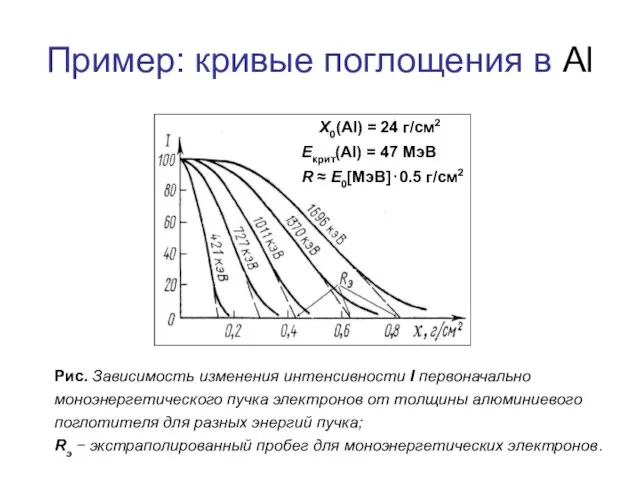
Пример: кривые поглощения в Al
Рис. Зависимость изменения интенсивности I первоначально моноэнергетического пучка электронов от толщины алюминиевого поглотителя для разных энергий пучка;
Rэ − экстраполированный пробег для моноэнергетических электронов.
X0(Al) = 24 г/см2
Eкрит(Al) = 47 МэВ
R ≈ E0[МэВ]⋅0.5 г/см2

Эксртаполированный пробег
Процессы рассеяния электронов и потери ими энергии, ведущие к уменьшению интенсивности, носят вероятностный характер, что приводит к значительному разбросу величин пробегов отдельных частиц. Для электронов в качестве средней величины пробегов, как правило, используют экстраполированный пробег, т. е. такую толщину поглотителя, при которой продолжение линейно спадающего участка зависимости интенсивности электронного пучка I(x) пересекает уровень нулевой интенсивности

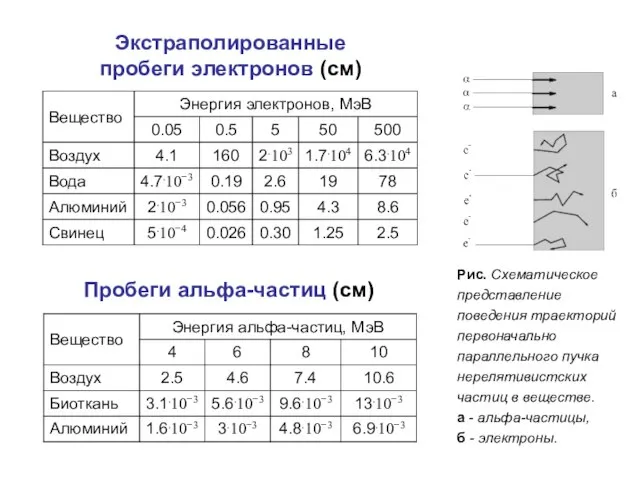
Экстраполированные
пробеги электронов (см)
Пробеги альфа-частиц (см)
Рис. Схематическое представление поведения траекторий первоначально параллельного пучка нерелятивистских частиц в веществе.
а - альфа-частицы,
б - электроны.

Раздел II.
5. Излучение Вавилова-Черенкова.
Излучение Вавилова-Черенкова (эффект Черенкова) – это электромагнитное излучение заряженной частицы при ее прямолинейном и равномерном движении в оптически прозрачной среде со скоростью υ > c/n, где n – показатель преломления среды.
Излучение было обнаружено аспирантом С.И.Вавилова – П.А.Черенковым в 1932 г. и объяснено физиками-теоретиками И.Е.Таммом и И.М.Франком в 1937 г.

Нобелевская премия по физике (1958 г.)
«За открытие и объяснение
эффекта Черенкова»
И.Е.Тамм, П.А.Черенков, И.М.Франк

История открытия
В 1932 г. аспирант П.А.Черенков под руководством С.И.Вавилова (директора ФИАН) приступил к исследованию люминесценции растворов ураниловых солей под действием γ-излучения от радиевого источника.
Сергей Иванович Вавилов
(1891 – 1951)
Павел Алексеевич Черенков
(1904 – 1990)

Люминесценция («холодный свет»):
интенсивность и спектр зависят от вещества, его чистоты и температуры;
излучение изотропно;
малые примеси некоторых веществ могут заметно уменьшать интенсивность люминесценции (эффект «тушения» - возбужденный атом вещества в силу конечного времени жизни передает энергию возбуждения молекуле примеси, а не излучает её в виде фотона).

Выполняя фоновые измерения с растворителями, Черенков обнаружил слабое голубое свечение со следующими свойствами (П.А.Черенков, ДАН СССР, 1934 г.):
интенсивность и спектр не зависят от вещества, его чистоты и температуры;
излучение связано с движением в среде электронов (это показали опыты с магнитным полем);
излучение направлено вдоль пучка электронов и поляризовано;
излучение имеет сплошной спектр с максимумом интенсивности в синей части спектра.

Первая попытка теоретического объяснения была предпринята Вавиловым (С.И.Вавилов, ДАН СССР, 1934 г.):
излучение связано с комптоновскими электронами, создаваемыми γ-квантами; ДА!
излучение имеет нелюминесцентный характер (т.е. не является испусканием фотонов атомами, возбужденными в результате столкновений с комптоновскими электронами); ДА!
излучение связано с торможением электронов. НЕТ! Интенсивность ТИ ~ Z2, а черенковского ~ Z0 =1!?
Объяснение

Правильное теоретическое объяснение эффекта Черенкова было дано сотрудниками ФИАН Таммом и Франком (И.Е.Тамм, И.М.Франк, ДАН СССР, 1937 г.)
Игорь Евгеньевич Тамм
(1895 – 1971)
Илья Михайлович Франк
(1908 – 1990)

Классическое рассмотрение (1-й вариант)
Согласно классической волновой теории, каждую точку траектории заряда, движущегося со скоростью υ в среде с показателем преломления n, можно рассматривать как источник
электромагнитных волн.
Оптическая разность хода 2-х волн:
Если cosθ≠1/βn, то всегда можно
подобрать AB, так что Δl=λ/2!!!
Если cosθ=1/(βn), то всегда Δl=0!!! ⇒ βn ≥ 1, т.е. υ ≥ c/n.

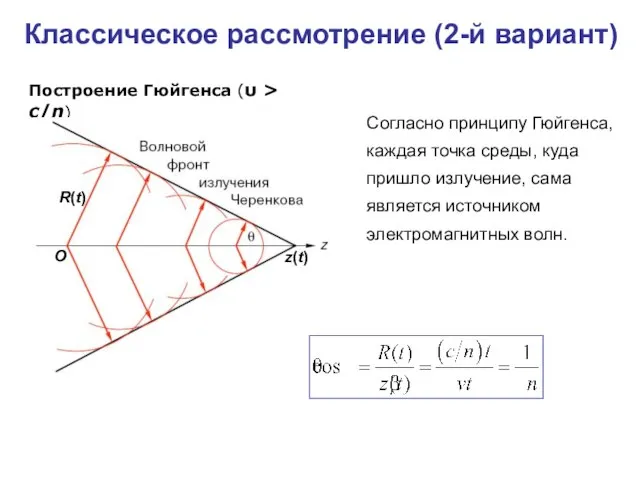
Классическое рассмотрение (2-й вариант)
Построение Гюйгенса (υ > c/n)
Согласно принципу Гюйгенса,
каждая точка среды, куда пришло излучение, сама является источником электромагнитных волн.

К принципу Гюйгенса (иллюстрация)
υ > c/n
υ < c/n

Аналогии
Фотография летящей пули, на которой виден фронт ударной волны.
Фотография самолета FA-18, на которой тоже виден конус ударной волны.
Эффект Черенкова имеет хорошо известные аналогии. Например, ударная волна, которая возникает при сверхзвуковой скорости (волны Маха). Кроме того, это волна, расходящееся от корабля, когда он движется со скоростью, большей скорости волн на воде.

Краткий экскурс в историю
Оливер Хевисайд
(Oliver Heaviside, 1850 - 1925)
В 1888 г. выдающийся английский физик Хевисайд рассмотрел движение заряда со скоростью υ > cэ, где cэ - скорость света в эфире. В частности, он предсказал «эффект Черенкова в эфире»!!!

Арнольд Зоммерфельд
(Arnold Sommerfeld, 1868 - 1951)
Уи́льям То́мсон, лорд Ке́львин
(William Thomson, 1st Baron Kelvin
1824 - 1907)
К аналогичным выводам пришли великий английский физик Кельвин (в 1901 г.), рассмотревший «сверхсветовой» атом, и выдающийся немецкий физик Зоммерфельд
(в 1904 г.), рассмотревший «сверхсветовой» электрон.

Альберт Эйнштейн
в 1905 г.
(Albert Einstein, 1879 - 1955)
В 1905 г. вышла в свет знаменитая работа Эйнштейна:
«Об электродинамике движущихся тел». Согласно этой работе, «сверхсветовые» частицы нарушают принцип причинности, а в эфире нет необходимости.
Таким образом, работы Хевисайда, Кельвина и Зоммерфельда стали «неактуальными».

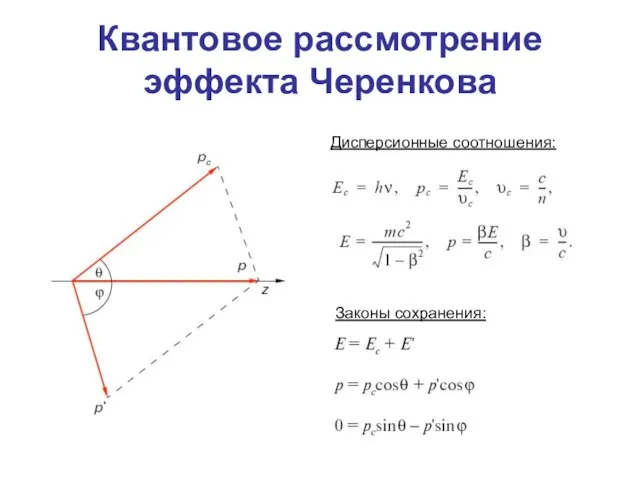
Квантовое рассмотрение эффекта Черенкова
Дисперсионные соотношения:
Законы сохранения:

Пример. В обычном стекле (n = 1,5) λзеленый ≈ 4∙10-7 м. Отсюда находим, что квантовая поправка к cosθ для зеленого фотона ~ 10-6.
Из законов сохранения энергии и импульса получаем:
В предельном случае υ = c/n (т.е. когда Λ = Λmax):
где λe = ħ/(mec) = 3,86∙10-13 м – комптоновская длина волны электрона.

Интенсивность и спектр
Решив уравнение Максвелла в среде, Тамм и Франк получили для энергии
черенковского излучения, испускаемого зарядом ze в интервале частот от
ω до ω+dω на участке пути dL:
Число фотонов, испускаемых в интервале от ω до ω+dω на участке пути dL:
Для большинства диэлектриков в рентгеновском диапазоне n(ω) < 1
(аномальная дисперсия), а в УФ области находится полоса поглощения ⇒
ωmax находится в близком ультрафиолете ⇒ максимум интенсивности
приходится на сине-фиолетовый участок спектра (это объясняет голубой
цвет черенковского свечения).

Угловой разброс
Учет дисперсии (зависимости показателя преломления от длины волны) будет приводить к угловому разбросу черенковского излучения. В случае нормальной дисперсии: nф > nк, т.е. показатель преломления для фиолетового цвета больше, чем для красного. Таким образом, для углового разброса имеем:

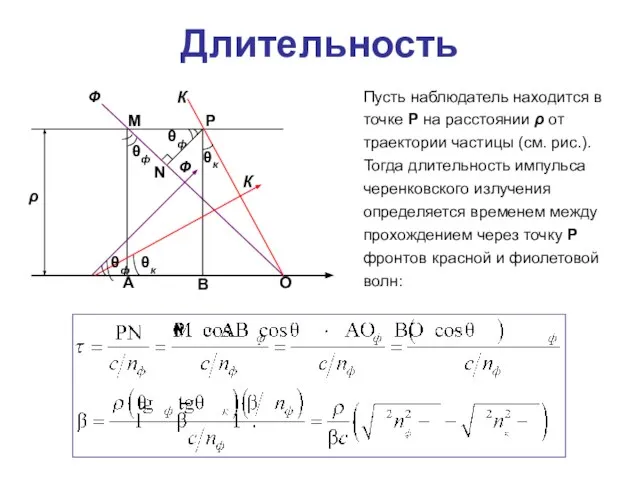
Длительность
ρ
Ф
К
Ф
К
P
M
N
O
A
B
θк
θк
θф
θф
θф
Пусть наблюдатель находится в
точке P на расстоянии ρ от
траектории частицы (см. рис.).
Тогда длительность импульса
черенковского излучения
определяется временем между
прохождением через точку P
фронтов красной и фиолетовой
волн:

Иллюстрация эффекта Черенкова
Фотография кольца черенковского света,
излученного в стекле пучком протонов с
энергий E = 660 МэВ. Центральное пятно
связано с прохождением пучка протонов
через фотопластинку. Фотография сделана в ОИЯИ (Дубна).

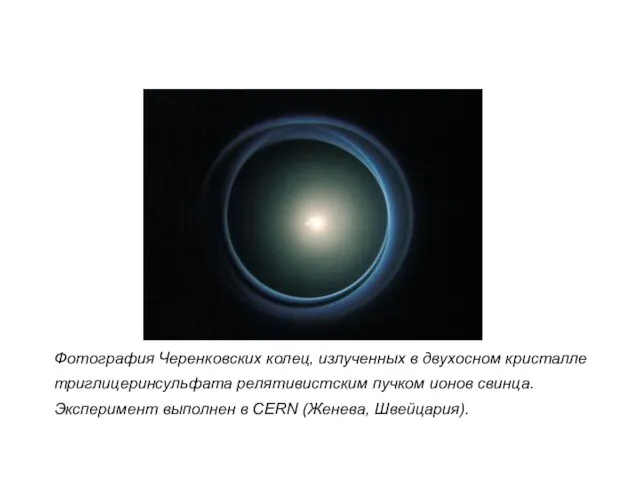
Фотография Черенковских колец, излученных в двухосном кристалле триглицеринсульфата релятивистским пучком ионов свинца. Эксперимент выполнен в CERN (Женева, Швейцария).

Раздел II.
6. Переходное излучение.
В 1945 г. Гинзбург и Франк теоретически предсказали испускание зарядом электромагнитного излучения при его прохождении через границу двух сред с разными показателями преломления (В.Л.Гинзбург, И.М.Франк, J. Phys. USSR, 1945 г.; ЖЭТФ, 1946 г.).
Виталий Лазаревич Гинзбург
(р. 1917)
Илья Михайлович Франк
(1908 – 1990)

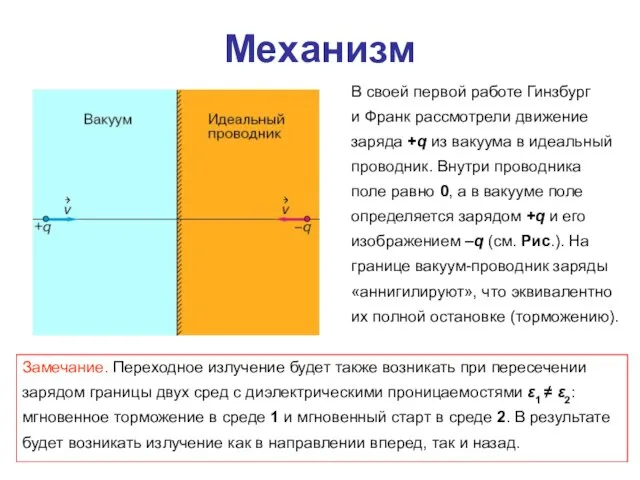
Механизм
В своей первой работе Гинзбург
и Франк рассмотрели движение
заряда +q из вакуума в идеальный
проводник. Внутри проводника
поле равно 0, а в вакууме поле
определяется зарядом +q и его
изображением –q (см. Рис.). На
границе вакуум-проводник заряды
«аннигилируют», что эквивалентно
их полной остановке (торможению).
Замечание. Переходное излучение будет также возникать при пересечении
зарядом границы двух сред с диэлектрическими проницаемостями ε1 ≠ ε2:
мгновенное торможение в среде 1 и мгновенный старт в среде 2. В результате
будет возникать излучение как в направлении вперед, так и назад.

В действительности никаких остановок и стартов заряда на границе 2-х сред не происходит: он движется с постоянной скоростью! На самом деле при пересечении границы 2-х сред скачком меняется фазовая скорость распространения электромагнитных волн: она равна c/n1 в 1-м диэлектрике и c/n2 во 2-м.
Таким образом, излучение происходит не только при изменении скорости частицы υ, но и при изменении скорости света, а точнее при изменении их отношения!
Переходное излучение представляет собой классический эффект, все свойства которого можно получить из уравнений Максвелла.
Задолго до работы Гинзбурга и Франка переходное излучение наблюдалось как белое «свечение» анодов в рентгеновских трубках, но оно было неверно интерпретировано.
В 1959 г. Голдсмит и Джелли наблюдали оптическое переходное излучение, образованное пучком протонов при пересечении металлической поверхности и показали, что его характеристики совпадают с предсказанными теорией Гинзбурга и Франка.

Основные характеристики
В результате расчета для спектральной плотности излучения нерелятивистского электрона в вакууме получается выражение
n2 = n + ik — комплексный показатель преломления
среды.
Для идеального проводника n2 → ∞ и, следовательно,
Рис. ПИ складывается из ТИ электрона, который внезапно останавливается (1) и стартует (2) на границе вакуум-среда, а также «изображения» (3), которое останавливается на границе вакуум-среда.
Т.е. максимум излучения приходится на φ = 90°.
Для реальных металлов и диэлектриков максимум излучения расположен при φ = 60°÷70°.

В ультрарелятивистском случае (E/m = γ >> 1) полная энергия переходного излучения при пересечении электроном границы вакуум-среда есть
Среднее число излучаемых фотонов есть
При этом ~ 1/2 фотонов испускается в рентгеновском диапазоне ω ≈ 0,1÷1⋅γωp!!!
Угловое распределение переходного излучения в рентгеновском диапазоне сосредоточено вблизи малого угла θ ≈ 1/γ в направлении «вперед». (В направлении «назад» излучаются в основном оптические фотоны).
Вероятность испускания одного переходного фотона очень мала – около 1/100 при пересечении частицей одной границы раздела сред. Поэтому для практического использования переходного излучения используются слоистые среды – пачки из тонких прозрачных пластинок, каждая из которых дает свой
вклад в излучение. При этом для E/m = γ >> 1 переходное излучение
попадает в рентгеновский диапазон и, следовательно, легко пронизывает всю пачку и может быть зарегистрировано рентгеновским счетчиком.
Ne – электронная плотность.

Детектор переходного излучения (ДПИ)
Рис. Схема одного из наиболее часто используемых ДПИ. Он состоит из нескольких модулей радиатор-детектор рентгеновских фотонов. Радиатор состоит из большого числа пленок с малым Z (для минимизации поглощения фотонов за счет фотоэффекта). Обычно стремятся, чтобы a и b превышали длины формирования излучения.

Длина формирования
Длина формирования L электромагнитной волны есть отрезок пути, на котором разность фаз излученных в данном направлении волн не превышает π. Т.е. все волны, испущенные на длине формирования, усиливают друг друга.
Пользуясь Рис., находим, что разность хода волн, испущенных в A и B, есть
По определению длины формирования, AB = L при Δ = λ/2. Отсюда

В интересующем нас случае излучения рентгеновских фотонов (ω >> ωp) ультрарелятивистской частицей (γ >> 1) имеем приближенно
Таким образом, получим следующие формулы для длин формирования излучения в среде (Lm) и вакууме (Lv):
Полагая θ = 1/γ, ω = γωp и υ = c, получим
Электроны с энергией 50 ГэВ, вполне доступные на современных ускорителях, имеют γ = 105. Для большинства материалов, используемых в рентгеновских счетчиках, ħωp ≅ 20 эВ и, следовательно, для таких электронов L ~ 1 мм.

Рассмотрим теперь переходное излучение, возникающее в плоскопараллельной пластинке толщиной a. Излучение будет иметь место как при входе заряженной частицы в пластинку, так и при выходе из нее. Если поглощением излучения в пластинке можно пренебречь и толщина пластинки a много меньше длины формирования излучения Lm, то волны, излученные от границ пластинки, будут в значительной степени «гасить» друг друга и интенсивность переходного излучения от пластинки будет много меньше, чем от одной границы. Качественно это легко объяснить, пользуясь аналогией между тормозным и переходным излучениями. Точные расчеты показывают, что для тонкой пластинки (a << Lm) интенсивность переходного излучения пропорциональна малой величине (a/Lm)2, а для толстой пластинки (a >> Lm) интенсивности излучения от обеих границ просто складываются. Таким образом, интенсивность излучения в толстой пластинке вдвое больше, чем от одной границы раздела. В промежуточном случае a ~ Lm имеют место сложные интерференционные эффекты.
Теперь нетрудно понять особенности переходного излучения в стопке из N пластин. Если толщины пластин и расстояния между ними много больше длин формирования излучения в веществе пластин и среде между ними, то суммарная интенсивность переходного излучения будет равна интенсивности излучения на одной границе, умноженной на число границ, то есть интенсивность увеличится в 2N раз. В противоположном случае тонких пластин и/или малого расстояния между ними необходимо учитывать интерференцию электромагнитных волн, испущенных с разных границ.

Раздел II.
7. Когерентное ТИ.
В отличие от аморфных веществ, где эффекты среды (поляризация, многократное рассеяние и т.д.) всегда приводят к подавлению тормозного излучения, в монокристаллах вследствие упорядоченного расположения атомов становится возможным относительное увеличение интенсивности тормозного излучения. Критерий появления когерентных эффектов состоит в том, что когерентная длина тормозного излучения Lc должна быть равна (или кратна) расстоянию d, проходимому быстрой частицей между последовательными столкновениями с атомами кристалла. При этом эффект усиления тормозного излучения (эффект Юберала; H. Überall, Phys.Rev. 103 (1956) 1055) по сравнению с излучением на изолированном атоме обусловлен когерентностью полей излучения, возникающих при рассеянии частицы на отдельных рассеивающих центрах.

Рис. Иллюстрация когерентного сложения амплитуд процессов излучения фотонов на системе периодически расположенных рассеивающих центров.
Рассмотрим излучение электромагнитных волн быстрой частицей, движущейся вдоль цепочки упорядоченных рассеивающих центров (Рис.). Амплитуды излучения фотонов на отдельных атомах An под нулевым углом к направлению движения частицы отличаются друг от друга на оператор сдвига:
где Δp|| – передаваемый кристаллу импульс в продольном направлении при излучении фотона.
При выполнении условия Δp||d = 2πħn (n=1,2,3…) амплитуды излучения фотонов на отдельных атомах будут иметь одинаковые фазы. В этом случае, в отличие от рассеяния на неупорядоченных рассевающих центрах, вероятность излучения будет пропорциональна квадрату числа атомов на длине траектории частицы.

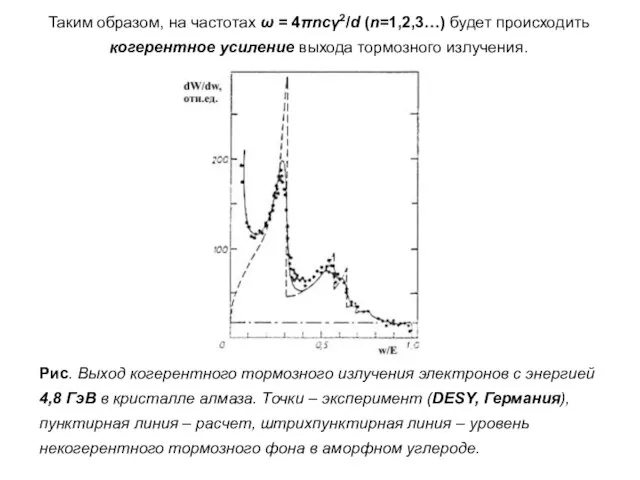
Рис. Выход когерентного тормозного излучения электронов с энергией 4,8 ГэВ в кристалле алмаза. Точки – эксперимент (DESY, Германия), пунктирная линия – расчет, штрихпунктирная линия – уровень некогерентного тормозного фона в аморфном углероде.
Таким образом, на частотах ω = 4πncγ2/d (n=1,2,3…) будет происходить когерентное усиление выхода тормозного излучения.

Раздел II.
8. Излучение каналированных e±.
Как и в случае тяжелых частиц, достаточно быстрые электроны и позитроны, т.е. дебройлевская длина волны которых много меньше постоянной решетки, могут каналироваться в монокристалле. В 1976 г. Кумаховым была впервые выдвинута идея об интенсивном рентгеновском и γ-излучении при каналировании релятивистских электронов и позитронов (эффект Кумахова; M.A.Kumakhov, Phys.Lett. A 57 (1976) 17). Эта идея была экспериментально подтверждена в 1978 г. в эксперименте на линейном ускорителе SLAC (Стэнфорд, США) по каналированию пучков позитронов с энергией в диапазоне 4–14 ГэВ в алмазе.

Основные свойства излучения Кумахова
В отличие от тормозного, черенковского и переходного излучений оно зависит от знака заряда.
В отличие от черенковского излучения оно зависит не только от скорости, но и от энергии частицы.
В отличие от тормозного излучения оно имеет ярко выраженные характерные частоты (пики), которые зависят от свойств частиц и кристалла.
Положение пиков в спектре меняется с изменением ориентации кристалла, угла наблюдения, энергии пучка.
В жестком рентгеновском и γ-диапазонах оно интенсивнее других типов излучения на 2-3 порядка.

Каналирование e±
Если заряженная частица влетает в кристалл под достаточно малым углом относительно направления его осей или плоскостей, она испытывает когерентное рассеяние на малые углы одновременно на большом количестве близлежащих атомов, и поэтому имеет относительно плавную траекторию движения. При этом положительно заряженные частицы отталкиваются от атомов оси или плоскости, а отрицательно заряженные – притягиваются. В результате характер движения и, следовательно, траектории частиц будут различными. Так, например, каналированные позитроны будут двигаться между двумя соседними плоскостями практически по синусоидальной траектории, рассеиваясь только на электронах кристалла, тогда как электроны будут пролетать через притягивающую их плоскость, соответственно более сильно рассеиваясь на ее атомах.

Непрерывное приближение
Для теоретических оценок можно с хорошей точностью заменить потенциал взаимодействия каналированной частицы с кристаллом усредненным потенциалом кристаллической оси (для осевого или, как еще говорят, аксиального каналирования) либо плоскости (для плоскостного или, как еще говорят, планарного каналирования).
d – расстояние между атомами оси;
V(x,y,z) – потенциал отдельного атома;
S – площадь, приходящаяся на один атом плоскости.

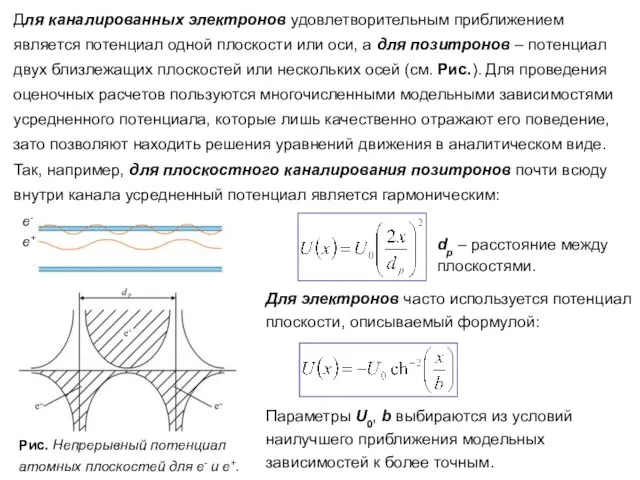
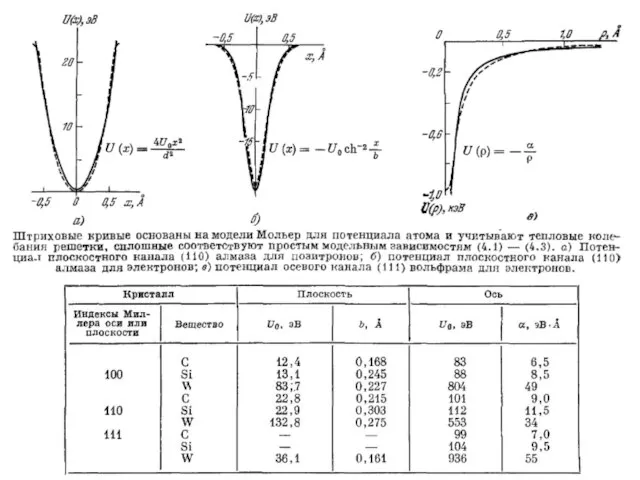
Для каналированных электронов удовлетворительным приближением является потенциал одной плоскости или оси, а для позитронов – потенциал двух близлежащих плоскостей или нескольких осей (см. Рис.). Для проведения оценочных расчетов пользуются многочисленными модельными зависимостями усредненного потенциала, которые лишь качественно отражают его поведение, зато позволяют находить решения уравнений движения в аналитическом виде. Так, например, для плоскостного каналирования позитронов почти всюду внутри канала усредненный потенциал является гармоническим:
e-
e+
Для электронов часто используется потенциал плоскости, описываемый формулой:
Рис. Непрерывный потенциал атомных плоскостей для e- и e+.
dp – расстояние между плоскостями.
Параметры U0, b выбираются из условий наилучшего приближения модельных зависимостей к более точным.

Угол Линдхарда
Важной характеристикой является критический угол каналирования ψL (угол Линдхарда). Критическим называется максимальный угол влета частиц в кристалл, при котором еще возможно каналирование. Поскольку усредненный потенциал зависит только от поперечных координат, энергию частицы, движущейся в кристалле, можно разделить на продольную E||, связанную с поступательным движением вдоль канала, и поперечную E⊥. С данной точки зрения частица считается каналированной, если ее поперечная энергия E⊥ меньше высоты барьера усредненного потенциала U0. Таким образом, в ультрарелятивистском случае имеем:
Характерная величина U0 («глубина» потенциальной ямы) определяется зарядом ядра, постоянной решетки, температурой Дебая и т.д. Типичное значение U0 для плоскостного канала (110) кремния составляет ~ 20 эВ, тогда как для вольфрама ~ 130 эВ. Потенциальная яма для осевого канала гораздо «глубже» (для кремния ~ 100 эВ, для вольфрама ~ 1000 эВ).

Длина деканалирования
Частицы в режиме каналирования, кроме малоуглового коррелированного рассеяния, ответственного за формировние траектории типа синусоиды (в плоскостном случае), испытывают рассеяние на большие углы, которое в конечном счете приводит к выбыванию частиц из канала (деканалированию). Характерная длина, на которой число каналированных частиц уменьшается в e раз, называется длиной деканалирования Ld. Длина деканалирования определяется как такая толщина кристаллической мишени, при прохождении которой среднеквадратичный угол многократного рассеяния сравнивается с критическим углом Линдхарда:
Из последнего соотношения следует, что длина деканалированния возрастает линейно с увеличением энергии начальной частицы.

Квантовые эффекты
В общем случае движение каналированных частиц должно описываться квантовыми уравнениями. Поскольку движение в поперечном направлении для каналированных частиц в потенциальной яме является финитным существуют дискретные уровни поперечной энергии. В диапазоне энергий электронов 1-10 МэВ в аксиальном и 1-100 МэВ в планарном случае для излучения существенны квантовые эффекты в каналировании. В данной области энергий спектр излучения имеет линейчатую структуру. Уравнение Шредингера для поперечного движения электрона в системе отсчета, где он в среднем покоится, в случае плоскостного каналирования имеет вид
E⊥, U(x) – поперечная энергия электрона и усредненный потенциал атомных плоскостей в лабораторной системе отсчета.

Эффект Доплера
Решение уравнения Шредингера даст уровни энергии, переходы между которыми определяют частоты излучения в системе отсчета, где электрон в среднем покоится:
В лабораторной системе отсчета частота излученного фотона, испущенного под углом θ к направлению движения электрона, есть (релятивистский эффект Доплера)
Максимальная энергия фотона реализуется при излучении прямо вперед:

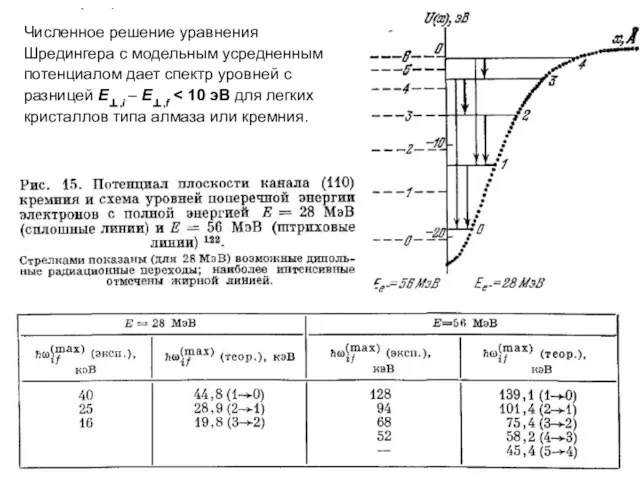
Численное решение уравнения Шредингера с модельным усредненным потенциалом дает спектр уровней с разницей E⊥,i – E⊥,f < 10 эВ для легких кристаллов типа алмаза или кремния.

Спектр излучения Кумахова
Из хорошо известной формулы излучения покоящегося квантового диполя, совершая преобразования Лоренца, для спектрально-угловой плотности мощности излучения при переходе между уровнями i и f, получаем
Интегрируя по углам излучения и суммируя по конечным состояниям, получим в ультрарелятивистском пределе

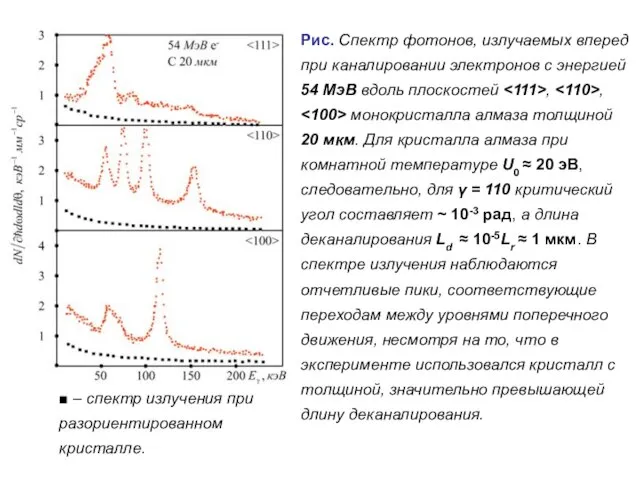
Рис. Спектр фотонов, излучаемых вперед при каналировании электронов с энергией 54 МэВ вдоль плоскостей <111>, <110>, <100> монокристалла алмаза толщиной
20 мкм. Для кристалла алмаза при комнатной температуре U0 ≈ 20 эВ, следовательно, для γ = 110 критический угол составляет ~ 10-3 рад, а длина деканалирования Ld ≈ 10-5Lr ≈ 1 мкм. В спектре излучения наблюдаются отчетливые пики, соответствующие переходам между уровнями поперечного движения, несмотря на то, что в эксперименте использовался кристалл с толщиной, значительно превышающей длину деканалирования.
■ – спектр излучения при разориентированном кристалле.

Удельные потери энергии
В дипольном приближении можно также получить удельные потери энергии ультрарелятивистской частицы на излучение при плоскостном каналировании:
Для плоскостного каналирования позитронов в параболическом потенциале:
Отсюда получим для удельных потерь:
ψ – угол между скоростью позитрона и атомными плоскостями при x = 0 (угол «влета» в канал). Таким образом, удельные потери энергии ~ γ2.

Классическая модель излучения
При достаточно высоких энергиях для описания движения частиц можно использовать классическую механику. Это связано с тем, что с ростом энергии число образующихся в плоскостном канале энергетических уровней n⊥ увеличивается по закону (в рамках модели потенциальной ямы «глубиной» U0)
Например, для электронов с энергией, превышающей 500 МэВ, число уровней в таких кристаллах, как кремний (U0 ~ 20 эВ), становится n⊥ > 20, что позволяет использовать классические подходы.
Классические уравнения движения позитрона в гармоническом потенциале плоскостного канала легко интегрируются и дают синусоидальную траекторию движения. Для данных траекторий в дипольном приближении можно легко рассчитать характеристики возникающего электромагнитного излучения.

Для простоты будем рассматривать ультрарелятивистский позитрон в плоскостном канале. В приближении постоянства продольной скорости (υz=const) релятивисткое уравнение движения в лабораторной системе имеет вид:
Решение этого уравнения легко находится в случае υz >> υx (т.н. дипольное приближение; см. также Раздел I, пункт 6, Основы релятивистской теории каналирования):
xmax – амплитуда колебаний позитрона в канале; ψ – угол между скоростью позитрона и атомными плоскостями при x = 0 (угол «влета» в канал).
Таким образом, задача об излучении позитрона в плоскостном канале сводится к задаче об излучении электрического диполя, который поступательно движется вдоль оси z и чей дипольный момент изменяется по гармоническому закону в поперечном направлении.

Общие выражения для спектрально-углового распределения дипольного излучения в классическом случае движения с периодом T получаются, согласно правилу соответствия Бора, заменой в квантовых выражениях матричных элементов xi→f фурье-компонентами поперечной координаты, а суммирование по конечным состояниям – суммированием по гармоникам n = 1,2,…:
Отсюда для спектральной плотности мощности излучения получим:
В рамках рассматриваемой модели параболического потенциала имеем

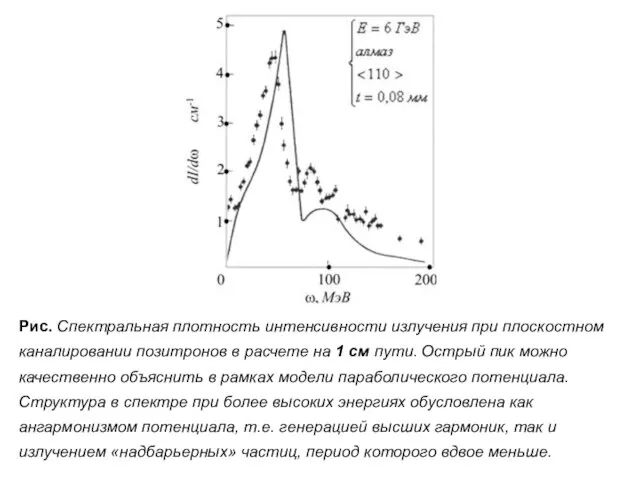
Рис. Спектральная плотность интенсивности излучения при плоскостном каналировании позитронов в расчете на 1 см пути. Острый пик можно качественно объяснить в рамках модели параболического потенциала. Структура в спектре при более высоких энергиях обусловлена как ангармонизмом потенциала, т.е. генерацией высших гармоник, так и излучением «надбарьерных» частиц, период которого вдвое меньше.

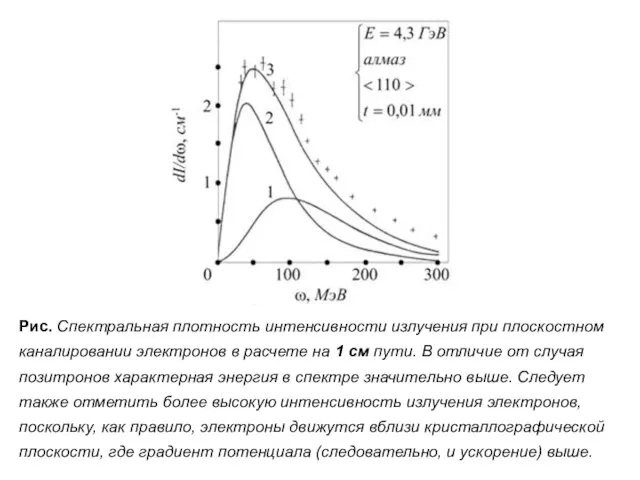
Рис. Спектральная плотность интенсивности излучения при плоскостном каналировании электронов в расчете на 1 см пути. В отличие от случая позитронов характерная энергия в спектре значительно выше. Следует также отметить более высокую интенсивность излучения электронов, поскольку, как правило, электроны движутся вблизи кристаллографической плоскости, где градиент потенциала (следовательно, и ускорение) выше.

Излучение при осевом каналировании электронов
Электроны, двигаясь в режиме осевого каналирования, проходят на близких расстояниях от кристаллографической оси, что приводит к существенному увеличению интенсивности излучения по сравнению с плоскостным каналом.
Спектр излучения при осевом каналировании является более жестким, чем при плоскостном. Характерная энергия фотонов в спектре излучения для осевого канала определяется минимальным расстоянием, на которое электрон приближается к оси, – радиусом экранирования rs:

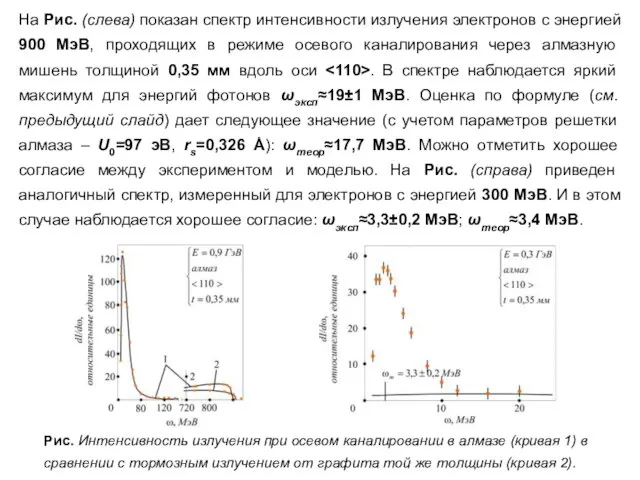
На Рис. (слева) показан спектр интенсивности излучения электронов с энергией 900 МэВ, проходящих в режиме осевого каналирования через алмазную мишень толщиной 0,35 мм вдоль оси <110>. В спектре наблюдается яркий максимум для энергий фотонов ωэксп≈19±1 МэВ. Оценка по формуле (см. предыдущий слайд) дает следующее значение (с учетом параметров решетки алмаза – U0=97 эВ, rs=0,326 Å): ωтеор≈17,7 МэВ. Можно отметить хорошее согласие между экспериментом и моделью. На Рис. (справа) приведен аналогичный спектр, измеренный для электронов с энергией 300 МэВ. И в этом случае наблюдается хорошее согласие: ωэксп≈3,3±0,2 МэВ; ωтеор≈3,4 МэВ.
Рис. Интенсивность излучения при осевом каналировании в алмазе (кривая 1) в сравнении с тормозным излучением от графита той же толщины (кривая 2).

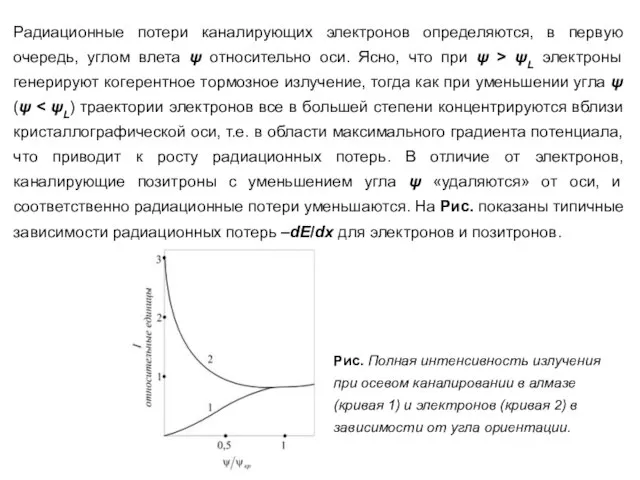
Радиационные потери каналирующих электронов определяются, в первую очередь, углом влета ψ относительно оси. Ясно, что при ψ > ψL электроны генерируют когерентное тормозное излучение, тогда как при уменьшении угла ψ (ψ < ψL) траектории электронов все в большей степени концентрируются вблизи кристаллографической оси, т.е. в области максимального градиента потенциала, что приводит к росту радиационных потерь. В отличие от электронов, каналирующие позитроны с уменьшением угла ψ «удаляются» от оси, и соответственно радиационные потери уменьшаются. На Рис. показаны типичные зависимости радиационных потерь –dE/dx для электронов и позитронов.
Рис. Полная интенсивность излучения при осевом каналировании в алмазе (кривая 1) и электронов (кривая 2) в зависимости от угла ориентации.

Оценку радиационных потерь для электронов при ψ = 0 можно получить, вычислив полные потери на излучение релятивистской частицы, движущейся в электростатическом потенциале U(r) (см. «Теория поля», §73, ф-ла (73,7)):
Отсюда следует
Через <…> обозначено усреднение градиента потенциала вдоль траектории. В качестве оценки этой величины можно взять выражение
где коэффициент x0 вычисляется для когерентного потенциала заданной кристаллографической решетки. Так, например, для алмаза x0 = 5,5 , тогда как для вольфрама x0 = 39,7.
Таким образом, можно записать

В отличие от тормозного излучения, где радиационные потери пропорциональны γ, для каналированных частиц имеем квадратичную зависимость. Можно сравнить радиационные потери при осевом каналировании электронов с энергией E = 1 ГэВ в кристалле алмаза (U0=97 эВ, rs=0,326 Å, x0=5,5) с радиационными потерями в процессе тормозного излучения в неориентированной алмазной мишени (Lr ≈ 12 см):
Таким образом, уже для энергии 1 ГэВ радиационные потери каналированных частиц примерно в 4 раза превышают потери в разориентированном алмазе.
Следует отметить, что процесс каналирования в чистом виде реализуется лишь для толщин кристаллов, сравнимых с длиной деканалирования. Для более толстых кристаллов (вплоть до толщин, сравнимых с радиационной длиной) основной вклад в излучение дает процесс когерентного тормозного излучения (КТИ).

с
Связь с когерентным ТИ
В рамках классического дипольного приближения можно получить
достаточно простые выражения для характеристик излучения как каналированными, так и надбарьерными электронами и позитронами. При движении в непрерывном потенциале плоскостей надбарьерные частицы излучают в результате последовательных столкновений с различными плоскостями, имеющими одинаковые индексы Миллера. Траектория таких частиц представляет периодическую кривую. Период ТаЬ совпадает со временем пролета между соседними плоскостями. Выражение для спектрального распределения излучения имеет формально такой же вид, как и для каналированных частиц. Однако характерные частоты и интенсивности излучения оказываются, вообще говоря, другими.
Рис. Траектории заряженной частицы в кристаллической решетке:
a – каналирование (ψ < ψL);
b – надбарьерный режим (ψ > ψL);
c – «неориентированный» режим (ψ >> ψL)

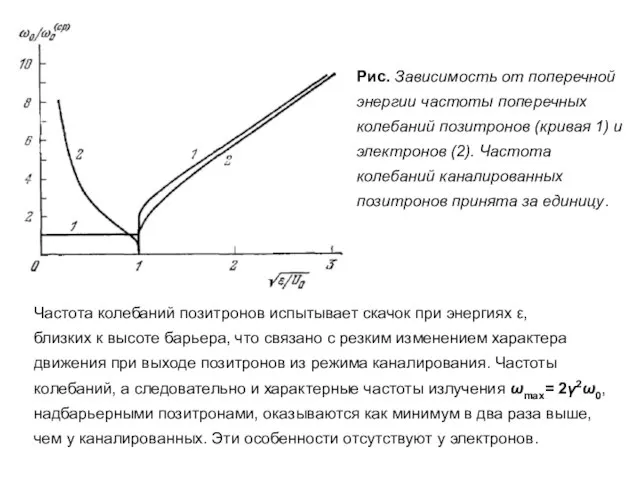
Рис. Зависимость от поперечной
энергии частоты поперечных колебаний позитронов (кривая 1) и электронов (2). Частота колебаний каналированных позитронов принята за единицу.
Частота колебаний позитронов испытывает скачок при энергиях ε,
близких к высоте барьера, что связано с резким изменением характера движения при выходе позитронов из режима каналирования. Частоты колебаний, а следовательно и характерные частоты излучения ωmах= 2γ2ω0, надбарьерными позитронами, оказываются как минимум в два раза выше, чем у каналированных. Эти особенности отсутствуют у электронов.