Содержание
- 2. Проблема конкурирующих гипотез и метод проб и ошибок Примеры гипотез: Встречу ли я динозавра, выйдя на
- 3. Проблема конкурирующих гипотез и метод проб и ошибок Примеры гипотез: Встречу ли я динозавра, выйдя на
- 4. Если мы вынули из ящика 21 белый шар, то это точно гипотеза H1 Но не обязательно
- 5. Проблема конкурирующих гипотез и метод проб и ошибок Примеры гипотез: Филогенетическая реконструкция: топология 1, топология 2
- 6. Проблема конкурирующих гипотез Решения: MP: выбираем наиболее простую гипотезу ML: выбираем наиболее правдоподобную гипотезу НО: 1)
- 7. Проблема конкурирующих гипотез А еще лучше иметь совокупность всех гипотез с прямыми оценками их вероятностей Есть
- 8. Метод Байеса (Bayes Inference) Thomas Bayes 1702-1761 England Байесова статистика . Обычная статистика рассматривает вероятности (частоты
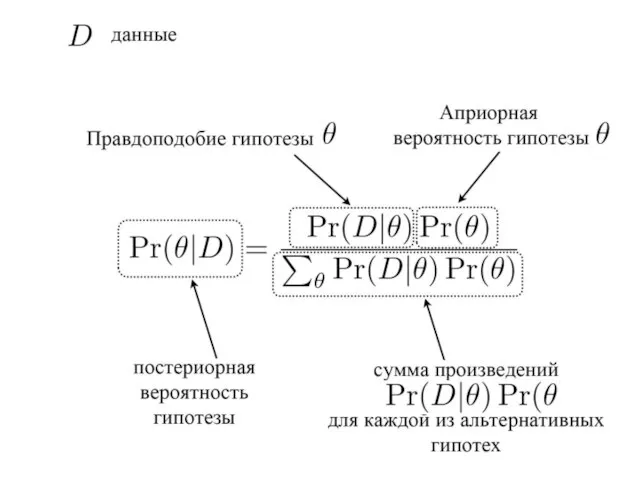
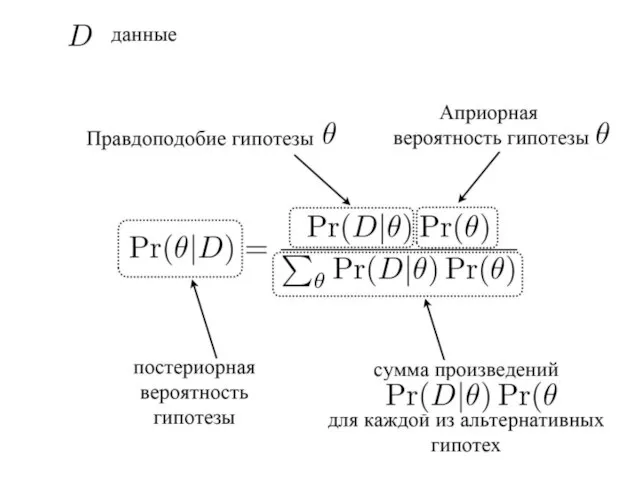
- 9. Метод Байеса (Bayes Inference) основные понятия: Априорная вероятность гипотезы Постериорная вероятность гипотезы правдоподобие гипотезы (вероятность наблюдения
- 10. Априорные и постериорные гипотезы Схема анализа: 1) выбираются (задаются) априорные гипотезы (вероятности) 2) получение данных (эмпирическое
- 11. H1 –гипотеза 1 Н2 – гипотеза 2 E - испытание (P(H1/E) – постериорная вероятность гипотезы H1
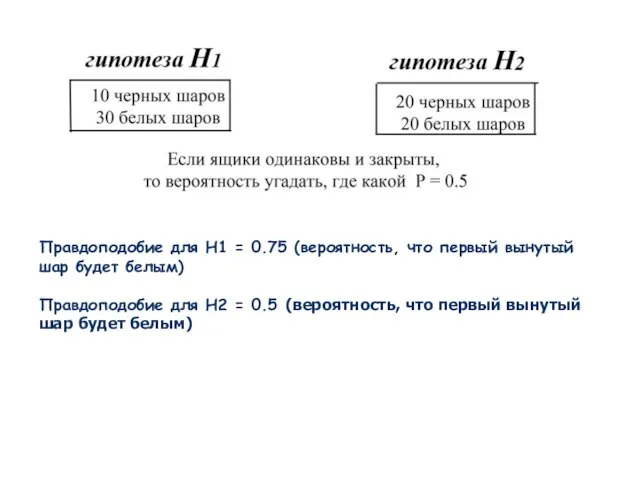
- 12. P априорное для H1 = 0.5 P априорное для H2 = 0.5
- 13. Правдоподобие для H1 = 0.75 (вероятность, что первый вынутый шар будет белым) Правдоподобие для H2 =
- 14. P(H1) – априорная вероятность гипотезы H1 (P(H1/E) – постериорная вероятность гипотезы H1 P(E/H1) – вероятность наблюдения
- 15. Итеративная процедура – многократное возвращение к тестированию исходной гипотезы, но каждый раз с учетом уже измененной
- 16. Вторая итерация априорные вероятности гипотез уже другие P(H1)=0.6; P(H2)=0.4 Р = (0.6 х 0.75)/(0.6 х 0.75
- 17. Р = (0.69 х 0.75)/(0.69 х 0.75 + 0.31 х 0.5) = 0.5175/(0.5175 + 0.155) =
- 18. Продолжаем процесс до тех пор пока вероятность одной из гипотез не достигнет 100% [P(H1)=1], т.е. гипотеза
- 19. Лодка затонула 21 мая 1968 годаЛодка затонула 21 мая 1968 года в 740 км (400 миль)
- 21. Как все это перенести на реконструкцию филогении? - нужны предварительные гипотезы - нужны значения правдоподобий
- 22. Метод максимального правдоподобия JC model Вероятности всех замен одинаковы, т.е. P(AC)=P(AG)=P(AT)=P(CG)=P(CT)=P(GT)=α частоты нуклеотидов равны, т.е. f(A)=f(C)=f(G)=f(T)=0.25
- 24. Теперь вопрос, как перейти к филогенетическим гипотезам, т.е. деревьям
- 25. • В филогенетике эволюционные модели составляют очень большое число гипотез: (каждая уникальная комбинация дерева [топологии] и
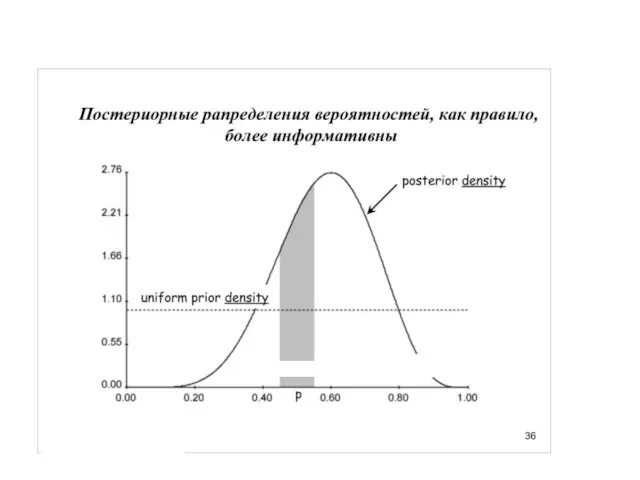
- 26. анализировать не отдельные гипотезы (их может быть неограниченное множество), а статистические распределения этих гипотез
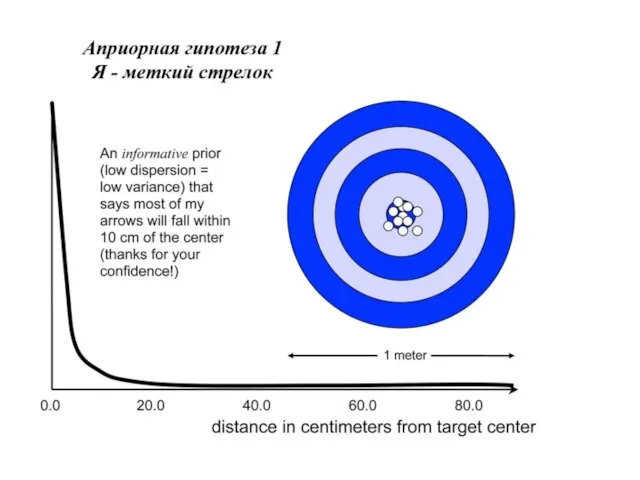
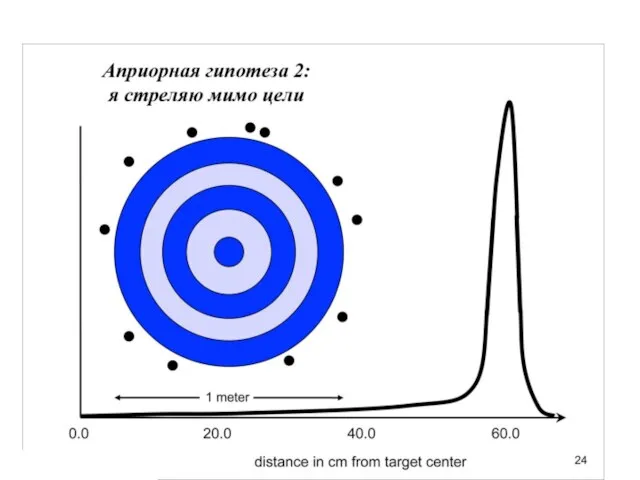
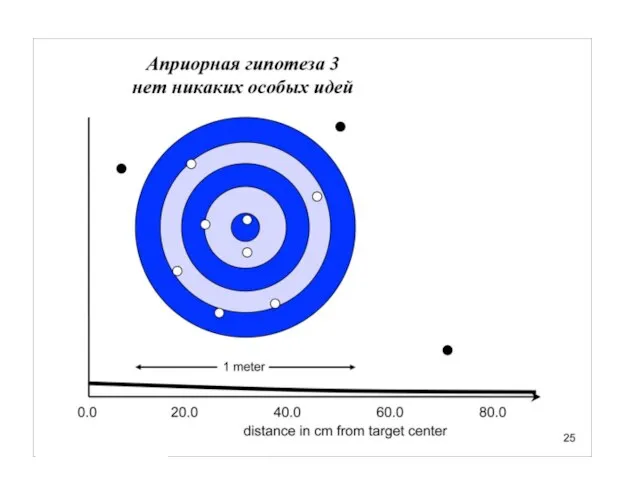
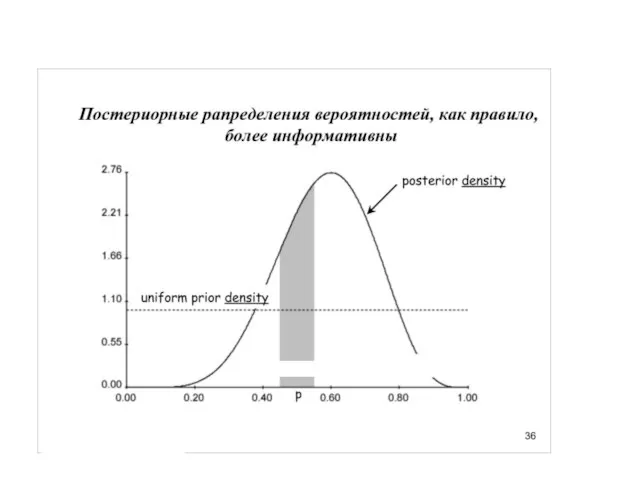
- 31. Униформный (неспецифический прайор), казалось бы, какая от него польза. Но вспомним про итеративность… Итерации постепенно сдвигают
- 33. Еще один прием: расчленить тестируемую гипотезу: представить ее в виде совокупности более простых гипотез
- 34. В случае филогенетической гипотезы вместо дерева можно дать совокупность: 1) топология 2) информация о длине ветвей
- 35. 1) прайор о топологии 2) прайор о длине ветвей 3) прайор о частотах нуклеотидов 4) прайор
- 37. При проведении анализа запускается несколько цепей (обычно 4), каждая из которых ищет оптимальные деревья Цепи могут
- 38. Как задать прайоры в Байесовом анализе? Как выбрать модель эволюции в Байесовом анализе? GTR+I+G
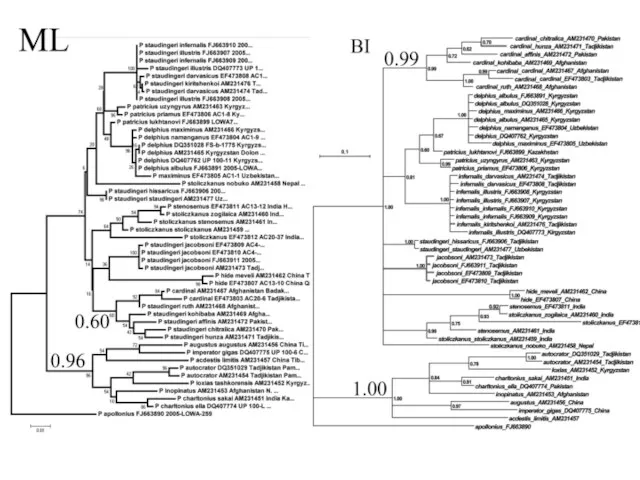
- 39. Пример Филогения бабочек рода Parnassius, основанная на анализе гена COI с использованием метода Байеса
- 42. но Основан на другой статистике, которая позволяет, получив вероятность дерева, пересчитать ее с учетом той топологии,
- 43. Получаемые в ходе Байесова анализа деревья образуют распределение, которое позволяет рассчитать так называемую постериорную вероятность отдельных
- 44. Распределение этих деревьев позволяет рассчитать так называемую апостериорную вероятность (PB), которая является прямой оценкой вероятности филогенетической
- 45. Методы максимального правдоподобия и Байеса: сходство и различия, плюсы и минусы ML говорит лишь о степени
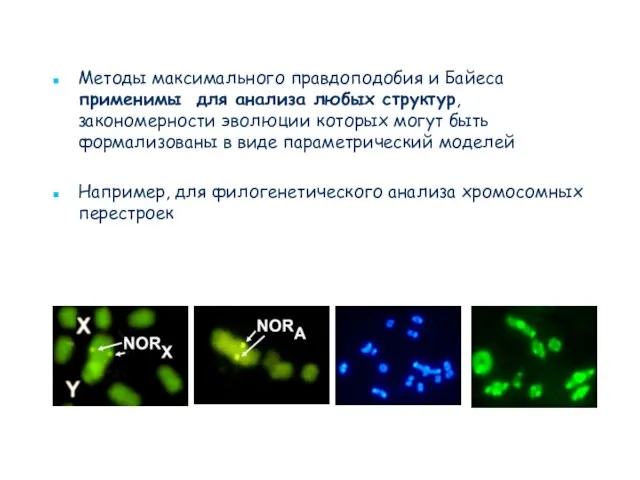
- 46. Методы максимального правдоподобия и Байеса применимы для анализа любых структур, закономерности эволюции которых могут быть формализованы
- 47. Не существует никакого теоретического запрета на использование морфологических признаков в рамках метода максимального правдоподобия и Байесова
- 48. Пример Филогения бабочек рода Parnassius, основанная на анализе гена COI с использованием метода Байеса
- 49. Методы реконструкции филогенезов , основанные на анализе генетических дистанций ДНК: 1 5 10 tagcaaaatg
- 50. Суть метода Откуда берутся генетические дистанции? ДНК-ДНК гибридизация, иммунологические реакции, анализ анонимных маркеров – все, что
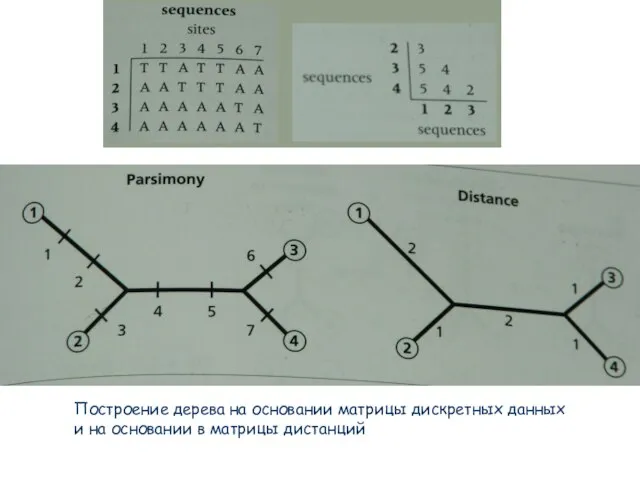
- 51. Превращение матрицы дискретных данных в матрицу дистанций Превращение матрицы дискретных данных в матрицу дистанций
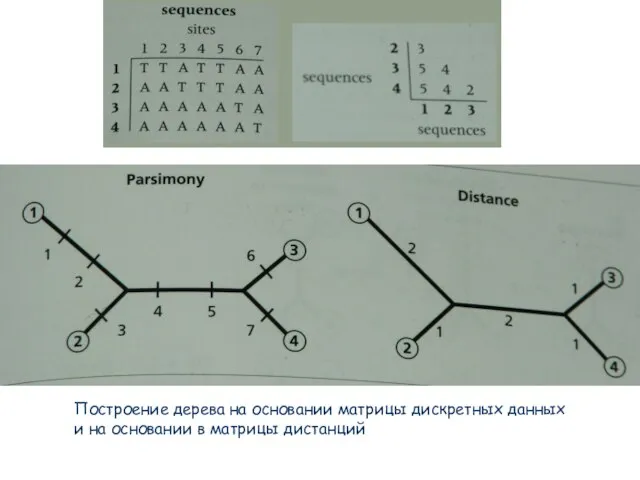
- 52. Построение дерева на основании матрицы дискретных данных и на основании в матрицы дистанций
- 53. Чем генетические дистанции отличаются от фенетических? Понятия сырой “p” дистанции и скорректированной дистанции модели эволюции
- 54. Методы коррекции генетических дистанций
- 55. Если вероятности нуклеотидных замен (p) и частоты нуклеотидов (f) константны во времени, то суммарная эволюционная дистанция
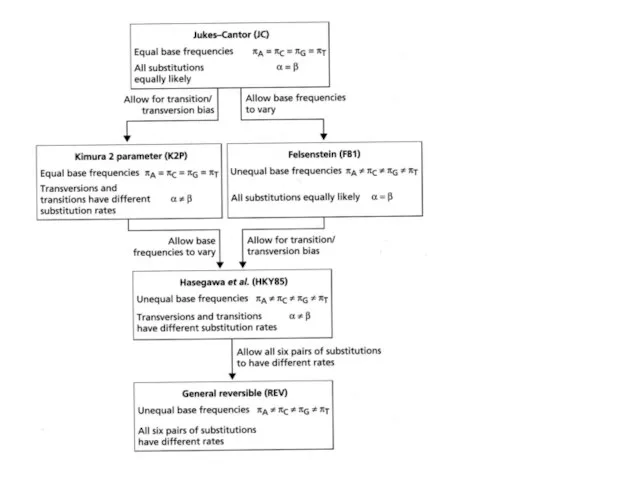
- 56. JC Вероятности всех замен одинаковы, частоты нуклеотидов равны
- 57. K2P Вероятности транзиций и трансверсий разные, частоты нуклеотидов равны α – транзиция β - трансверсия
- 58. F81 Вероятности всех замен одинаковы, но частоты нуклеотидов разные
- 59. K2P Вероятности транзиций и трансверсий разные, частоты нуклеотидов разные
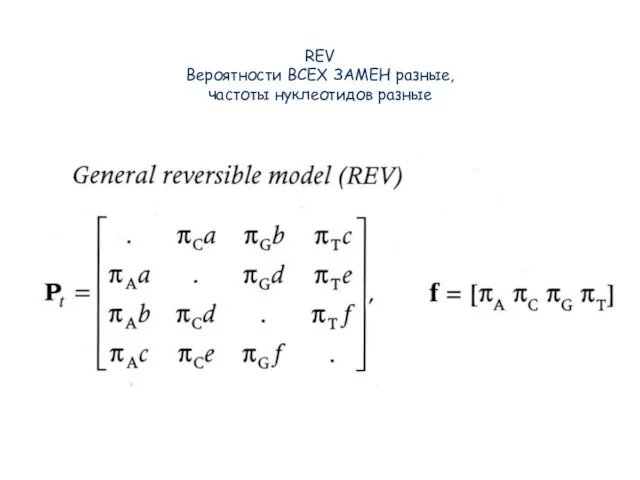
- 60. REV Вероятности ВСЕХ ЗАМЕН разные, частоты нуклеотидов разные
- 62. Методы построения “дистантных” деревьев Методы основанные на использовании критериев оптимальности Методы, основанные на алгоритмах кластеризации
- 63. Методы основанные на использовании критериев оптимальности Метод наименьших квадратов Оптимальным деревом признается то, при котором сумма
- 65. Методы основанные на использовании критериев оптимальности Метод наименьших квадратов Оптимальным деревом признается то, при котором сумма
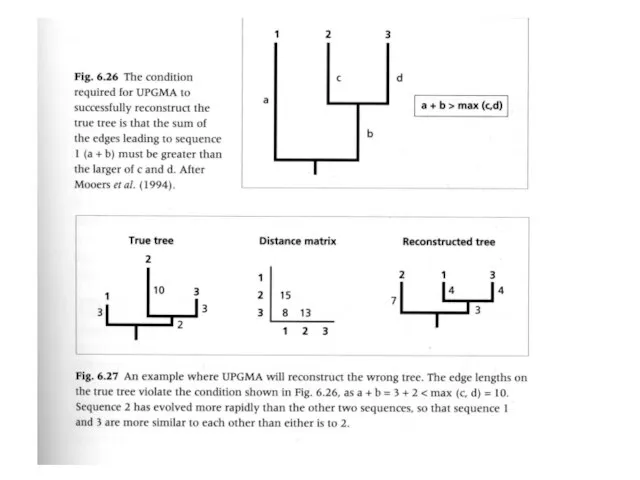
- 66. Методы, основанные на алгоритмах кластеризации Метод ближайшего соседа (Neighbour Joining) Метод UPGMA (unweighted pair group method
- 67. Построение дерева на основании матрицы дискретных данных и на основании в матрицы дистанций
- 68. Методы, основанные на алгоритмах кластеризации Метод ближайшего соседа (Neighbour Joining) Метод UPGMA (unweighted pair group method
- 71. Скачать презентацию



















































 УАТТ ДЖЕЙМС (1736–1819)
УАТТ ДЖЕЙМС (1736–1819) Физика 7
Физика 7 Разработка проектной идеи образовательного ресурса. №3
Разработка проектной идеи образовательного ресурса. №3 Хумус Бар
Хумус Бар Лекция 7
Лекция 7 Презентация на тему Гаршин сказка о жабе и розе
Презентация на тему Гаршин сказка о жабе и розе  Презентация на тему Белки
Презентация на тему Белки Презентация на тему Применение жиров
Презентация на тему Применение жиров  Первомайская центральная районная детская библиотека
Первомайская центральная районная детская библиотека Чудо Земли - хлеб
Чудо Земли - хлеб Бытовой жанр в русской живописи конца ХVIII в. - первой половины ХIХ в
Бытовой жанр в русской живописи конца ХVIII в. - первой половины ХIХ в Выставка работ
Выставка работ Отчет о проделанной работе с резидентами по дисциплине Клиническая фармакология, 2019-2021 годы обучения
Отчет о проделанной работе с резидентами по дисциплине Клиническая фармакология, 2019-2021 годы обучения 孔子学院在乌克兰和俄罗斯
孔子学院在乌克兰和俄罗斯 Презентация на тему Саудовская Аравия
Презентация на тему Саудовская Аравия  Методические рекомендации к заполнению классного журнала в государственном образовательном учреждении общего образования
Методические рекомендации к заполнению классного журнала в государственном образовательном учреждении общего образования Представление нечисловой информации
Представление нечисловой информации Дед Мороз на новогодних открытках
Дед Мороз на новогодних открытках Разветвляющийся алгоритм
Разветвляющийся алгоритм Пролог к изучению поэмы Н.В. Гоголя «Мертвые души»
Пролог к изучению поэмы Н.В. Гоголя «Мертвые души» Познавательные процессы (память)
Познавательные процессы (память) Диспансеризация сельскохозяйственных животных при внутренних болезнях
Диспансеризация сельскохозяйственных животных при внутренних болезнях Инвестиционная деятельность предприятия
Инвестиционная деятельность предприятия «МОЯ СТРАНА – МОЯ РОССИЯ»
«МОЯ СТРАНА – МОЯ РОССИЯ» Любовная лирика Ф.И.Тютчева
Любовная лирика Ф.И.Тютчева Нестероидные противовоспалительные средства
Нестероидные противовоспалительные средства Почему болеют мои одноклассники
Почему болеют мои одноклассники Штат Колорадо
Штат Колорадо