Разложение электромагнитного поля резонатора по пространственно локализованным базисным функциям

Электромагнитные взаимодействия описаны в тер-минах трехмерного (скалярно-векторного) потенци-ального формализма, Для краткости все уравнения приведены для векторного потенциала
Переход к полевому формализму:
Уравнение Д’Аламбера:
Уравнение непрерывности тока:

В работе исследуется прямоугольный резонатор с однородными граничными условиями (ГУ) первого, второго рода или периодичности на всех границах для всех составляющих потенциала
Решение уравнения Д’Аламбера осуществляется путем разложения потенциала в ряд по базисным функциям резонатора, зависящим от пространственных координат
Основным приближением модели является финитность спектра потенциала в области волновых чисел, обеспечивающая конечность указанного ряда

Наиболее известными базисными функциями являются собственные функции резонатора, определяемые как решения задачи о собственных значениях для оператора Лапласа –2 :
Ряд по собственным функциям называется рядом Фурье. Поскольку уравнение Д’Аламбера допускает разделение переменных, без ограничения общности далее можно рассматривать двух- или одномерную колебательную систему
Условие ортогональности собственных функций:

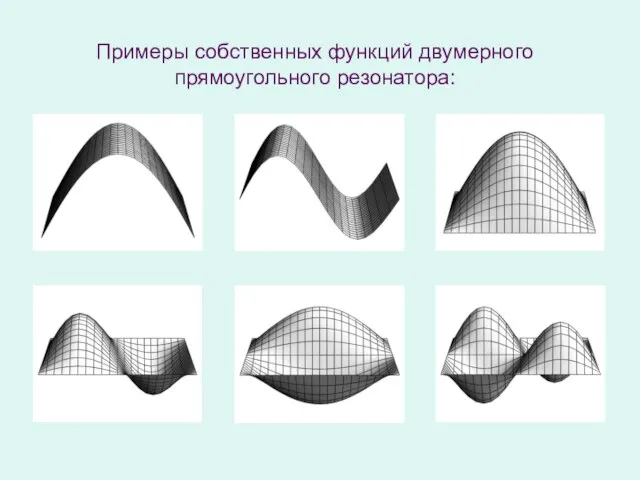
Примеры собственных функций двумерного прямоугольного резонатора:

Достоинство собственных функций – ортогональ-ность, позволяющая решать задачу о собственных значениях независимо для каждой из функций.
Недостаток – распределенность в пространстве, приводящая к медленной сходимости ряда Фурье для потенциала коротких (сверхширокополосных) электромагнитных импульсов
Эквивалент уравнения Д’Аламбера при разложении потенциала по собственным функциям:

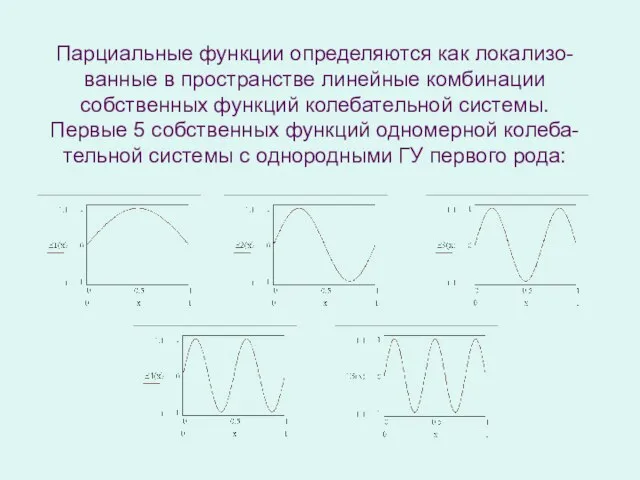
Парциальные функции определяются как локализо-ванные в пространстве линейные комбинации собственных функций колебательной системы.
Первые 5 собственных функций одномерной колеба-тельной системы с однородными ГУ первого рода:

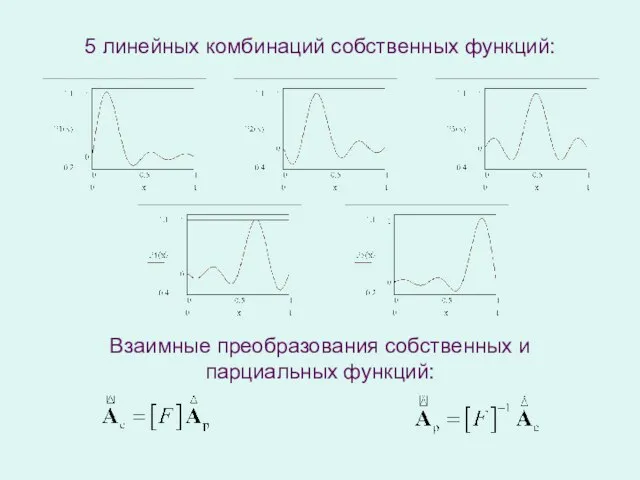
5 линейных комбинаций собственных функций:
Взаимные преобразования собственных и парциальных функций:

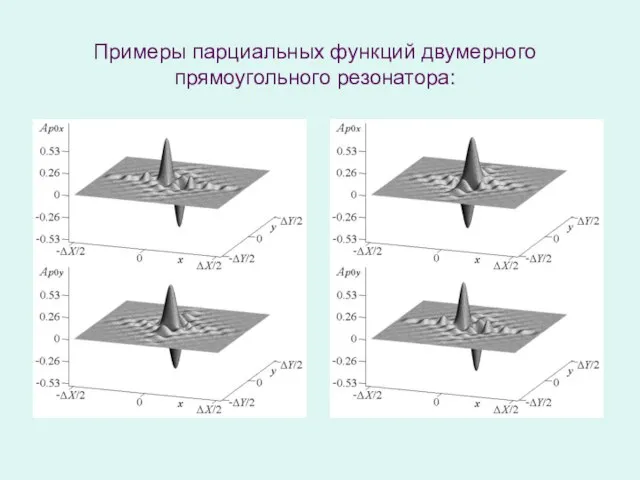
Примеры парциальных функций двумерного прямоугольного резонатора:

Задача о m-м собственном значении матрицы N×N взаимных волновых чисел парциальных осцилляторов (m = 0 … N – 1) :
Парциальные функции можно определить также как локализованные в пространстве решения задачи о взаимных значениях для оператора Лапласа –2 :
Fem – m-й собственный вектор матрицы взаимных волновых чисел, он же m-я строка матрицы [ F ]

Расчет матрицы взаимных значений:

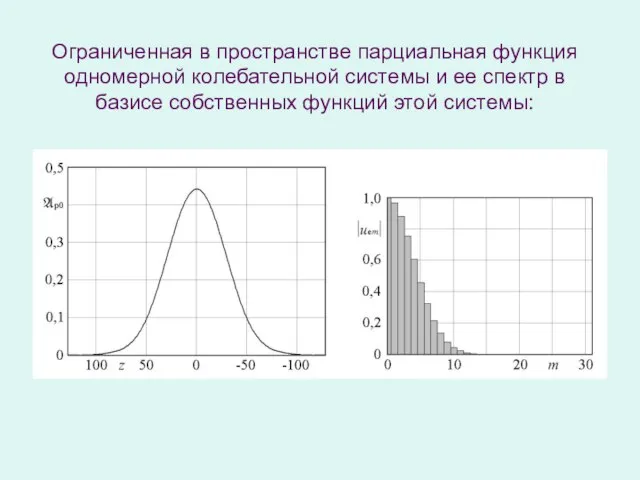
Ограниченная в пространстве парциальная функция одномерной колебательной системы и ее спектр в базисе собственных функций этой системы:

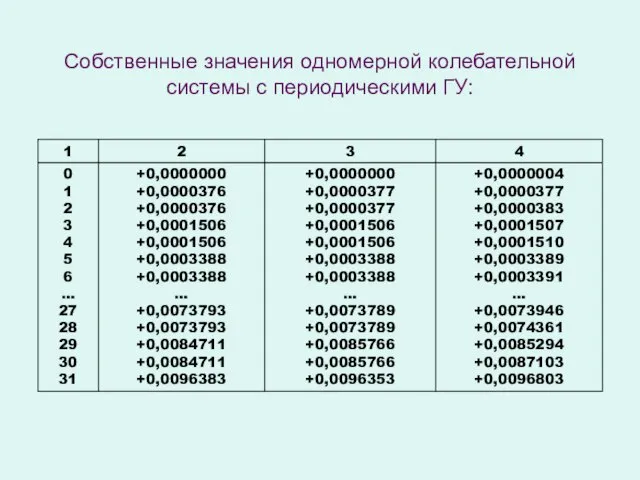
Собственные значения одномерной колебательной системы с периодическими ГУ: