Развертки поверхностей

1. Общие сведения
Развертка поверхностей - преобразование, в результате ктр. все точки развертываемой поверхности совмещаются с одной плоскостью без искажений.
В этом случае поверхность называется развертываемой, а развертка – точной, либо приближенной.
Поверхности, ктр. не могут быть совмещены с одной плоскостью без искажений, относятся к неразвертываемым поверхностям, а поэтому их развертка называется условной.

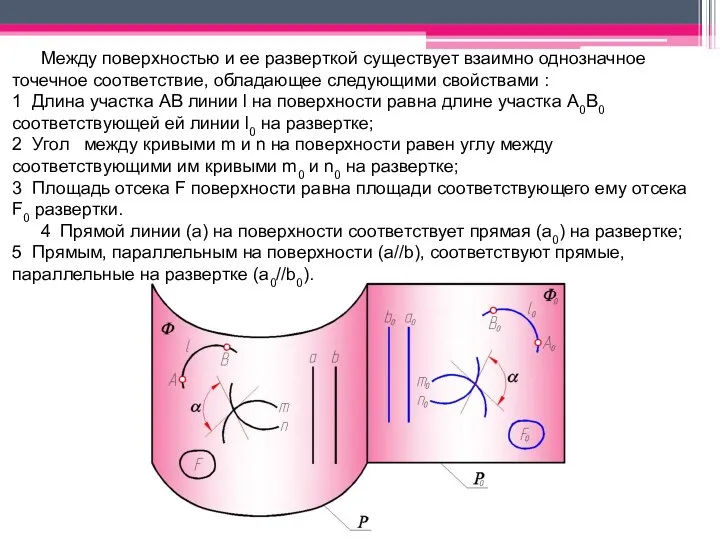
Между поверхностью и ее разверткой существует взаимно однозначное точечное соответствие, обладающее следующими свойствами :
1 Длина участка АВ линии l на поверхности равна длине участка А0В0 соответствующей ей линии l0 на развертке;
2 Угол между кривыми m и n на поверхности равен углу между соответствующими им кривыми m0 и n0 на развертке;
3 Площадь отсека F поверхности равна площади соответствующего ему отсека F0 развертки.
4 Прямой линии (a) на поверхности соответствует прямая (а0) на развертке;
5 Прямым, параллельным на поверхности (а//b), соответствуют прямые, параллельные на развертке (a0//b0).

2. Методы построения разверток гранных поверхностей
Разверткой поверхности многогранника называют плоскую фигуру, полученную при совмещении с плоскостью всех его граней.
Для построения развертки многогранника необходимо найти натуральные величины всех его ребер.
Для построения развертки боковой поверхности применяют следующие методы:
1. Метод треугольников (триангуляции) (для пирамид);
2. Метод раскатки (вращают грани призмы последовательно вокруг одного ребра до совмещения с плоскостью чертежа – получают боковые ребра призмы и основания в натуральную величину);
3. Метод перпендикулярного (нормального) сечения.

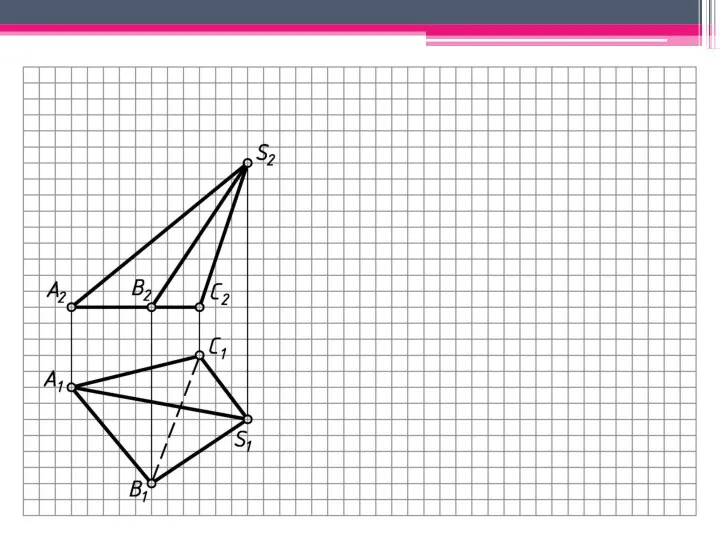
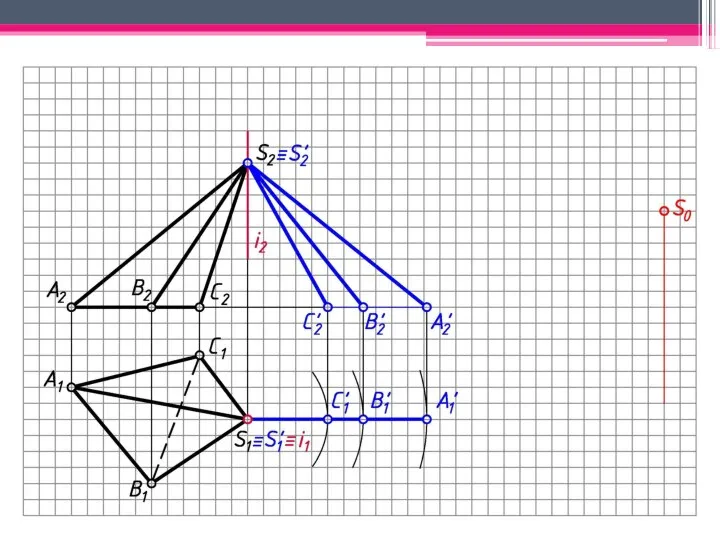
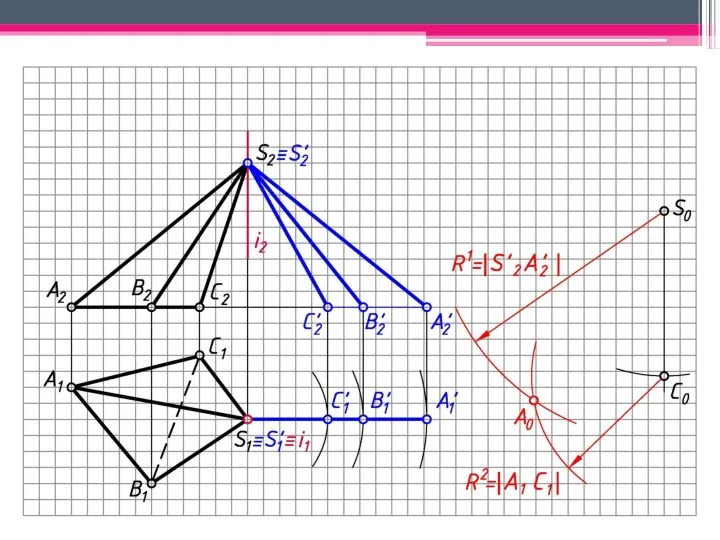
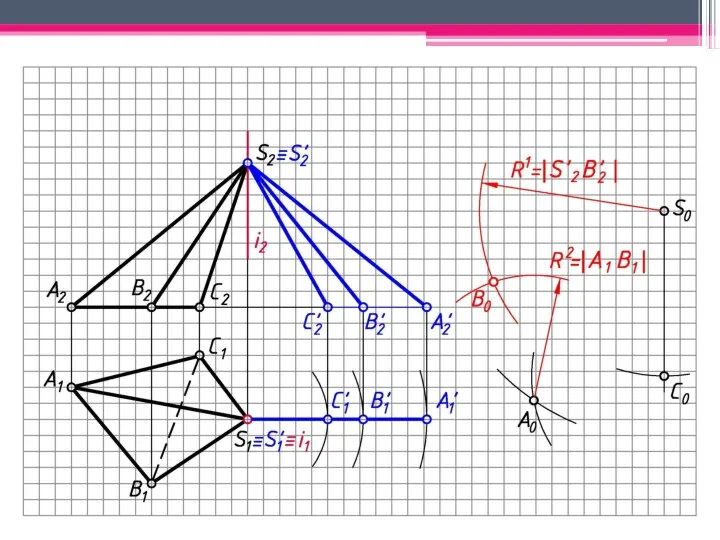
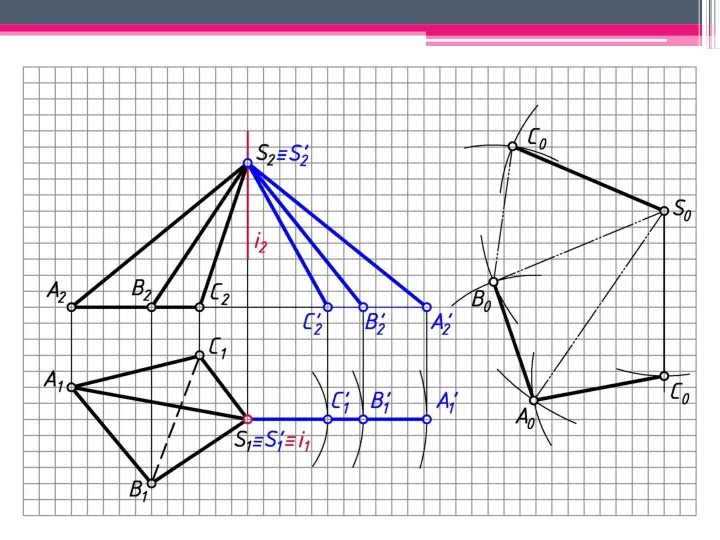
МЕТОД ТРЕУГОЛЬНИКА
Определяем н.в. всех ребер пирамиды вращением вокруг гор.-проец. оси i (i1; i2). S’2A’2; S’2В’2; S’2С’2 – н.в. Т.к. АВС – пл. гор. уровня, то А1В1С1 – н.в.
На свободном поле чертежа отмечаем точку S0 и через нее проводим произвольную линию.
От S0 на линии откладываем н.в. ребра SC = |S’2С’2 |.
А0 = Окр. (ц. S0; R1= |S’2A’2 |) ∩ Окр. (ц. C0; R2= |А1С1 |).
Аналогичным образом определяем другие точки.
Линии сгиба показываем штрихпунктирной линией с двумя штрихами.
К развертке боковой поверхности пирамиды пристраиваем н.в. основания.

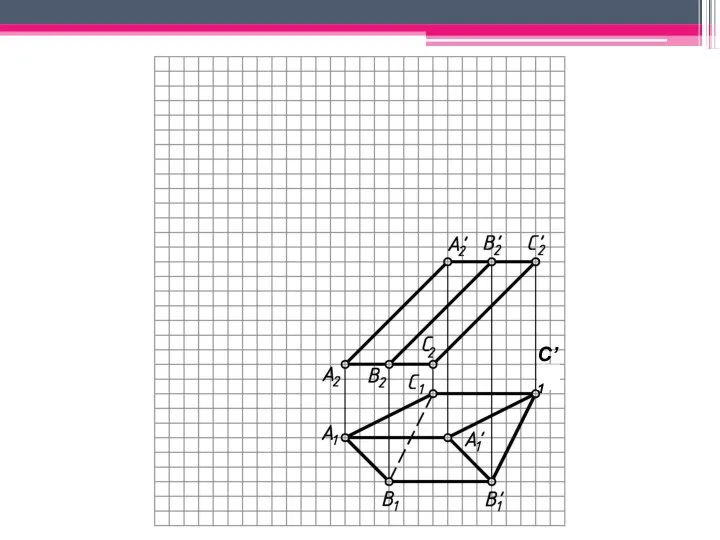
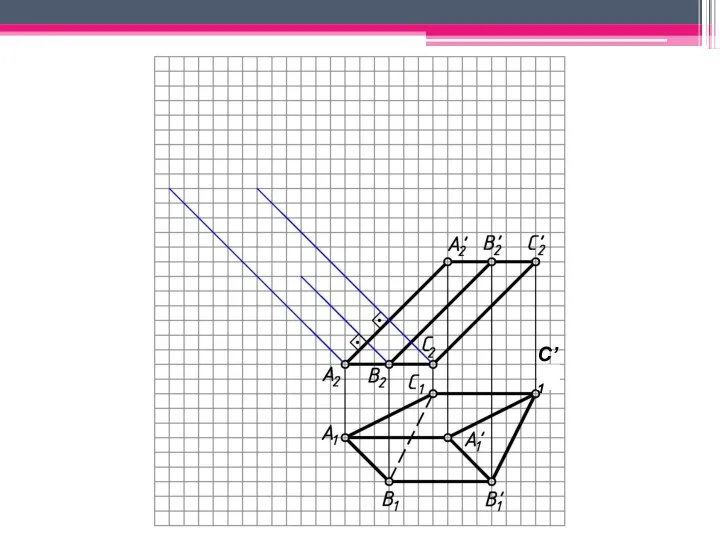
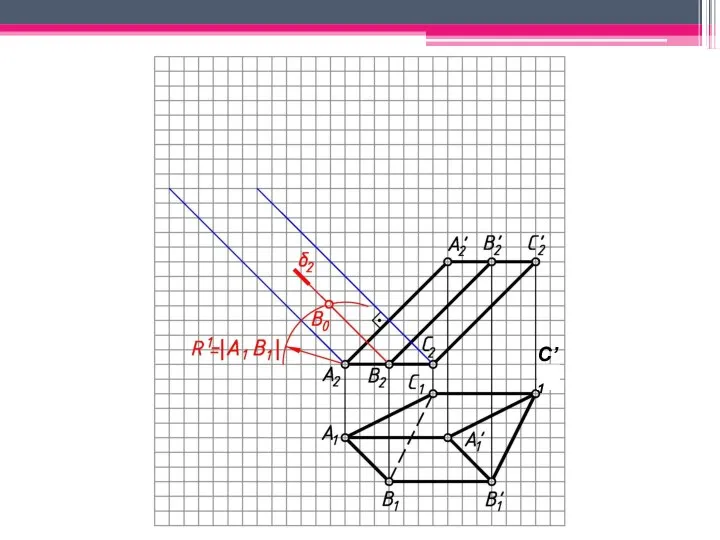
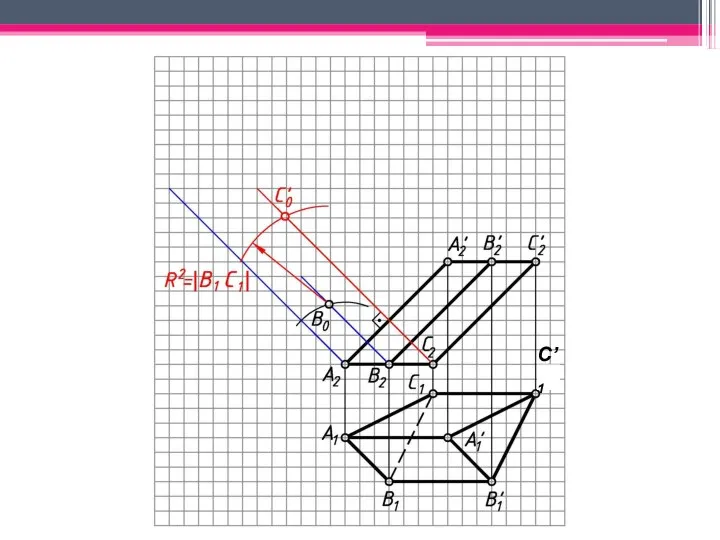
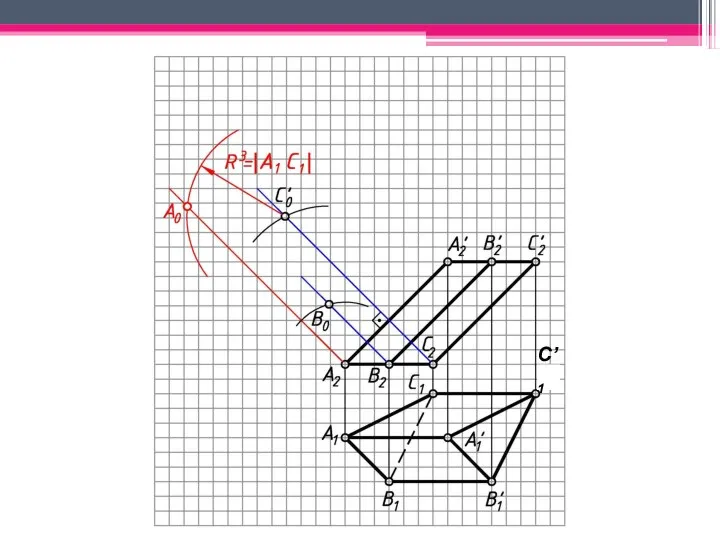
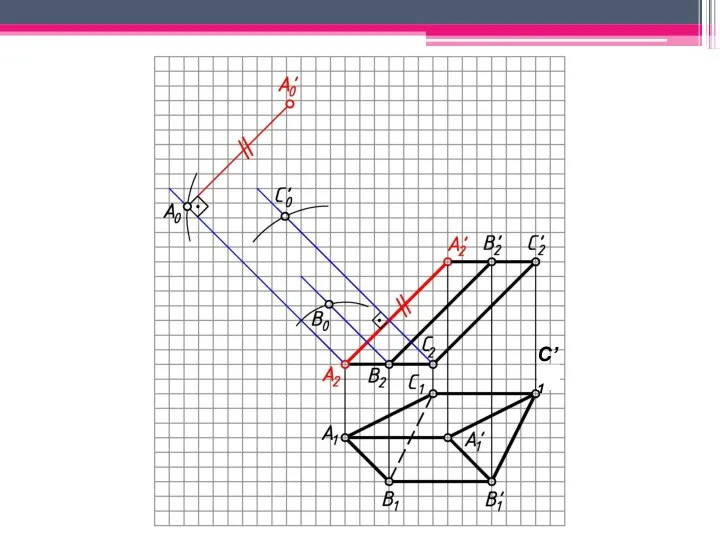
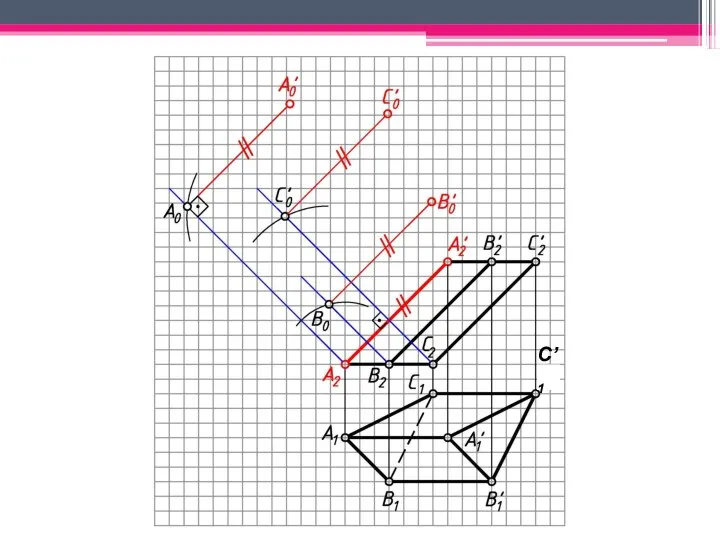
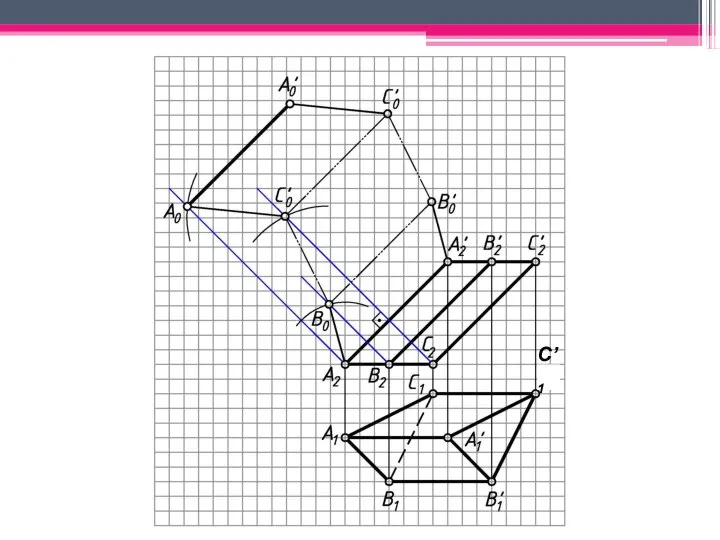
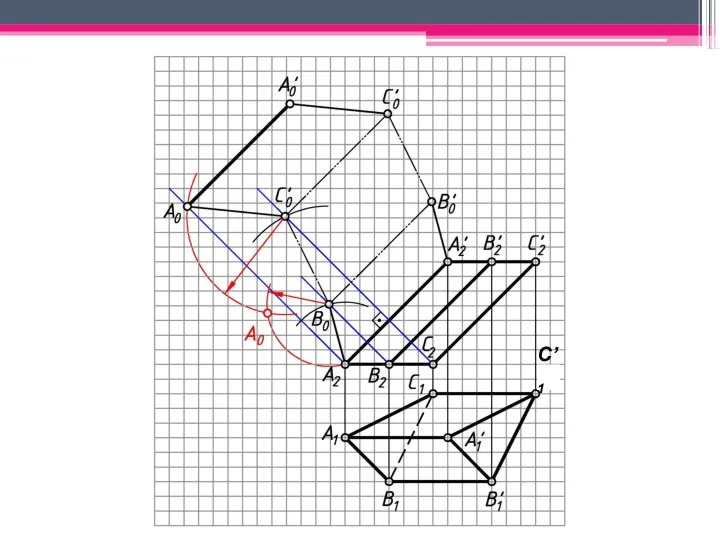
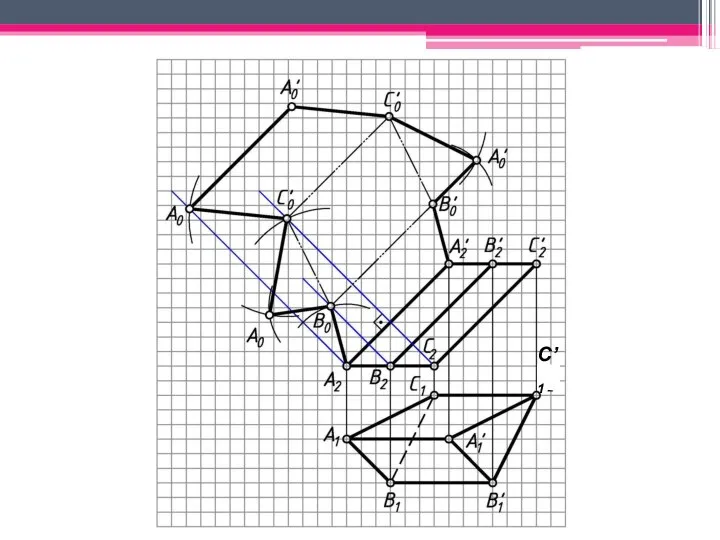
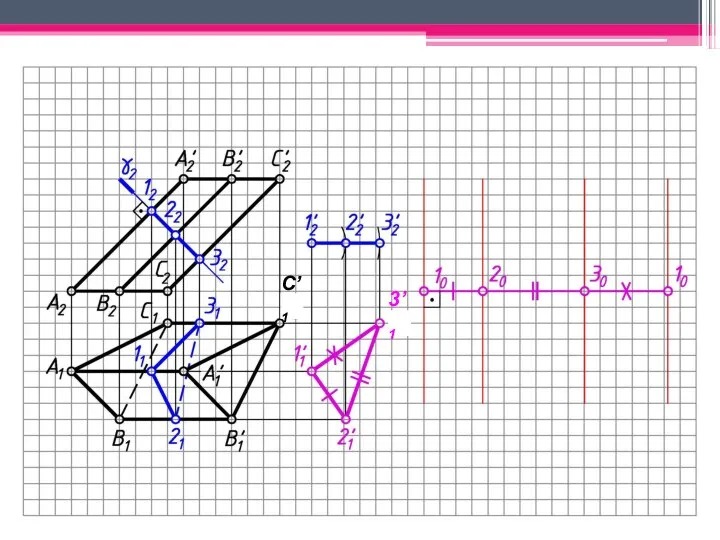
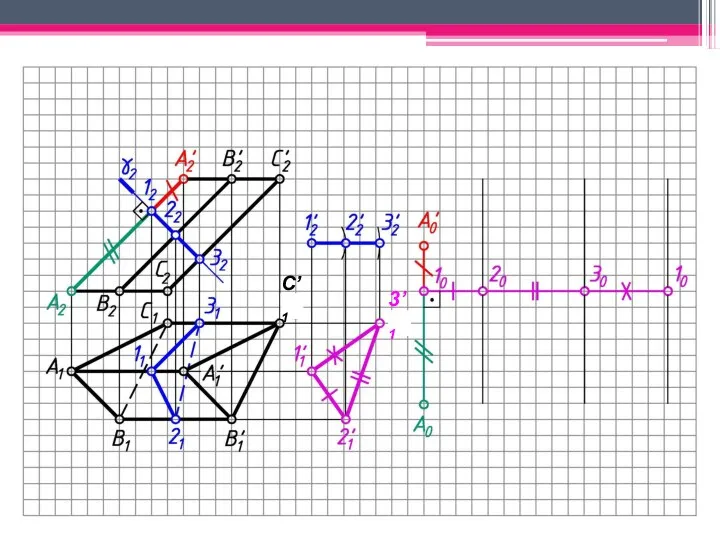
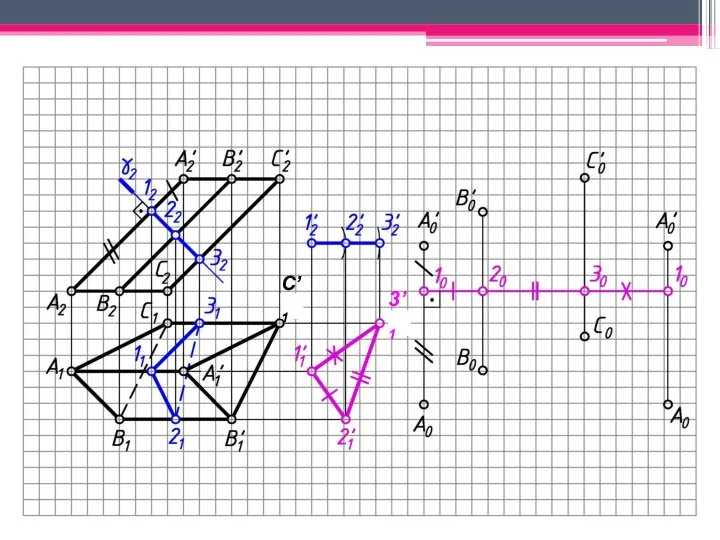
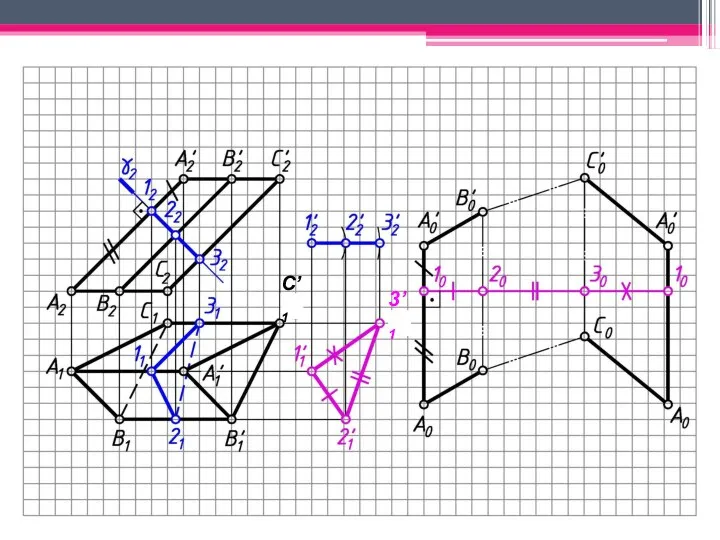
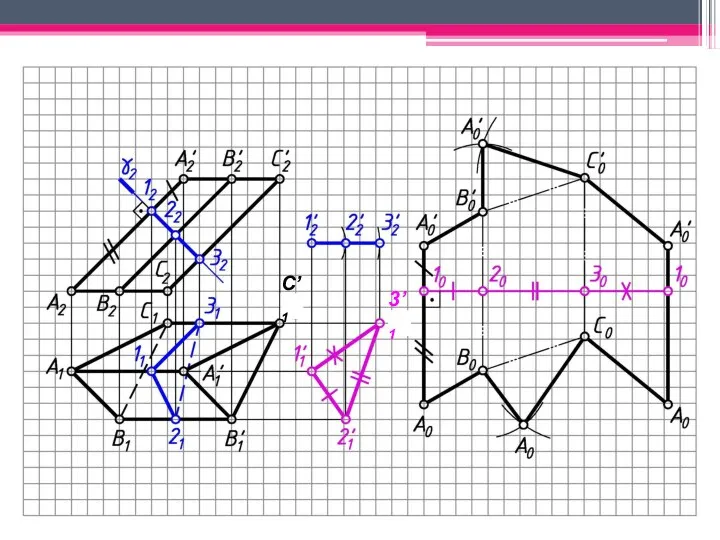
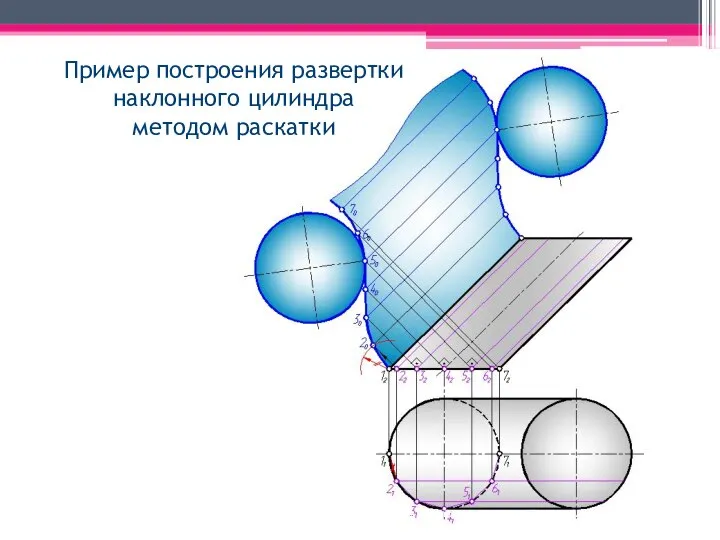
МЕТОД РАСКАТКИ
А2A’2; В2В’2; С2С’2 – н.в., т.к. АА’, BB’, CC’ – прямые фронт. уровня. Т.к. АВС – пл. гор. уровня, то А1В1С1 – н.в.
Из проекций А2, В2, С2 проводим плоскости вращения, ⊥-но А2А’2.
Последовательно вращаем т. В, до совмещения с пл. фронт. уровня, проходящей через ребро А2А’2 (см. вращение вокруг следа плоскости): А2А’2 - ось вращения, А2 – центр вращения; R1= |А1В1 | - н.в. радиуса вращения. Вращаем т.В до пересечения с ее плоскостью вращения δ2.
Другие точки строим аналогично.
А0А’0 || А2А’2 ; |А0А’0 | = |А2А’2 |;
Аналогично строим другие ребра призмы.
К развертке боковой поверхности призмы пристраиваем основания.

С’1

С’1

С’1

С’1

С’1

С’1

С’1

С’1

С’1

С’1

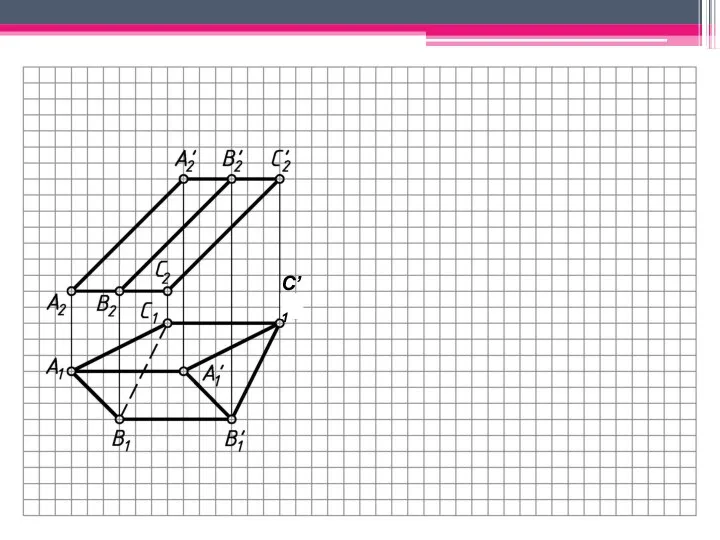
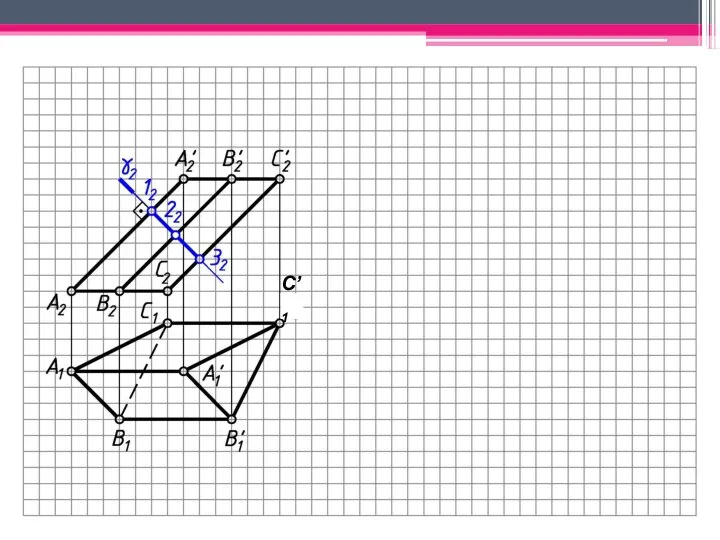
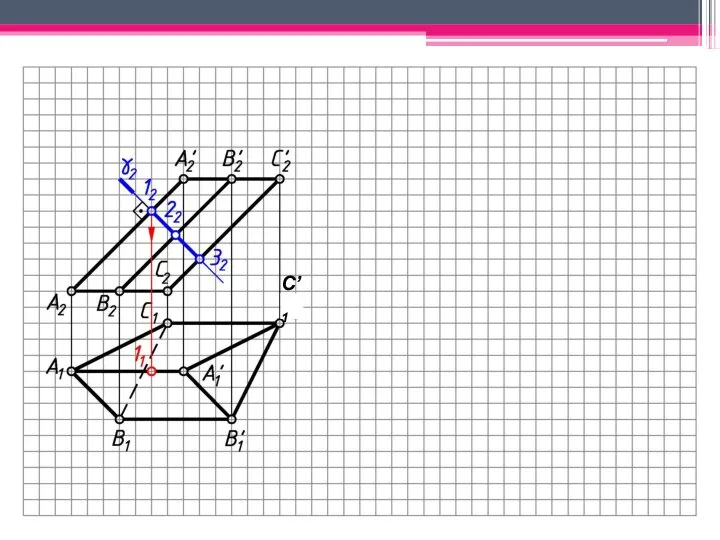
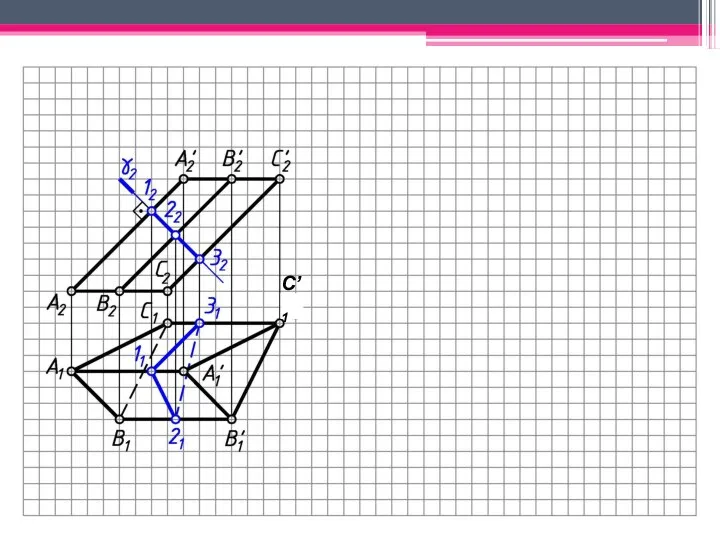
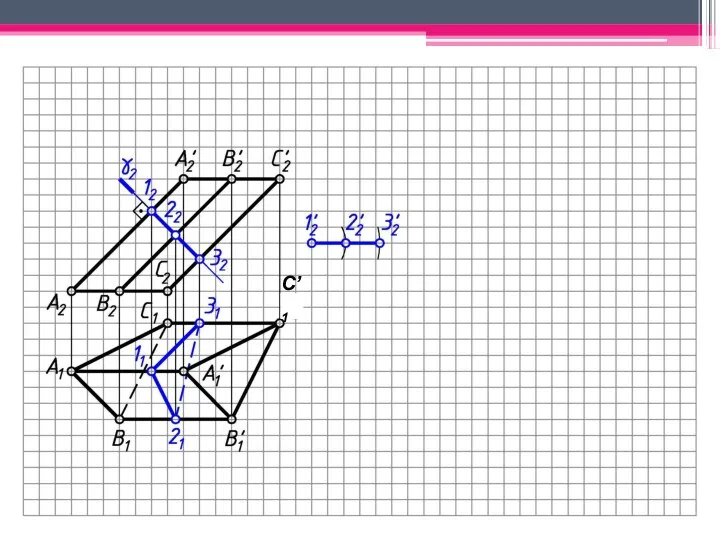
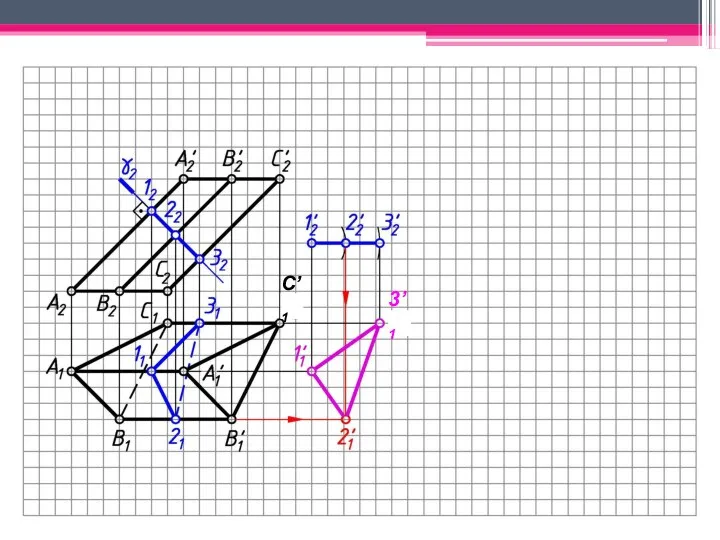
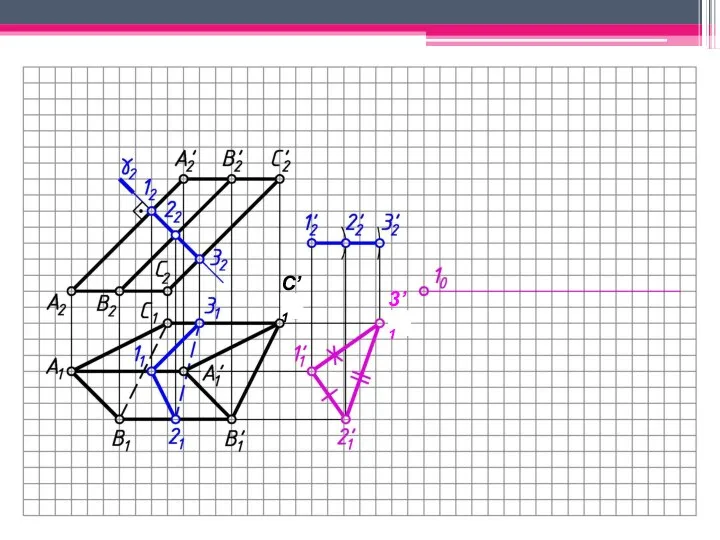
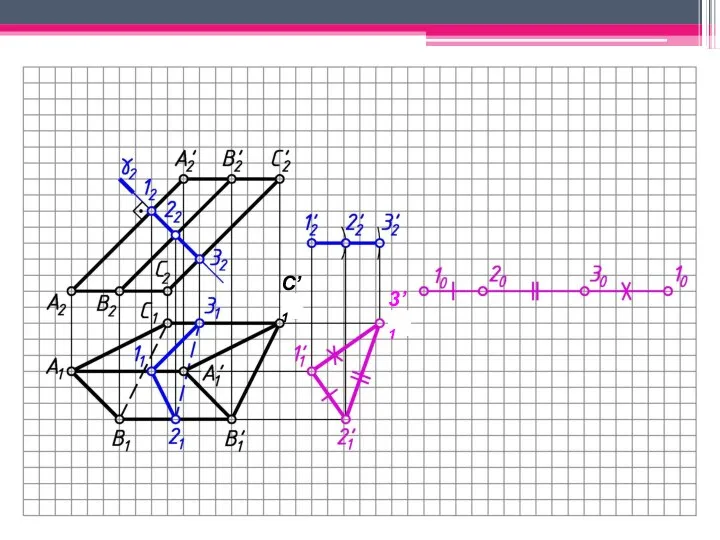
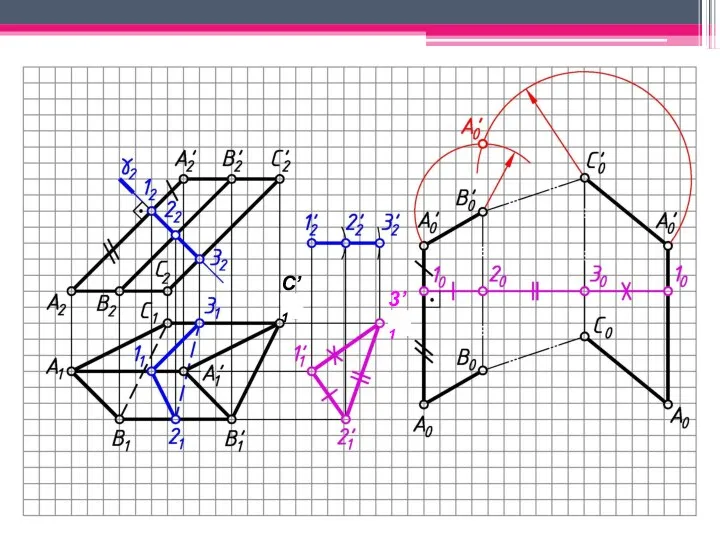
МЕТОД ПЕРПЕНДИКУЛЯРНОГО СЕЧЕНИЯ
А2A’2; В2В’2; С2С’2 – н.в., А1В1С1 – н.в.
Проводим произвольно фронт.-проец. пл. γ - γ2 ⊥ А2А’2 .
123 – линия пересечения γ с призмой.
Определяем н.в. 123 способом плоскопараллельного перемещения. 1’12’13’1 – н.в. 123.
Проводим на свободном поле чертежа горизонтальную линию и откладываем на ней действительные величины всех сторон перпендикулярного сечения.
Из точек 10, 20, 30 проводим вертикальные линии, на ктр. последовательно откладываем 10А0 = |12А2 | и 10А’0 = |12А’2 |.
Аналогично строим другие ребра призмы.
К развертке боковой поверхности призмы пристраиваем основания.

С’1

С’1

С’1

С’1

С’1

С’1
3’1

С’1
3’1

С’1
3’1

С’1
3’1

С’1
3’1

С’1
3’1

С’1
3’1

С’1
3’1

С’1
3’1

3. Методы построения разверток криволинейных поверхностей
Для построения развертки конической поверхности осуществляется ее аппроксимация пирамидальной поверхностью.
Развертка этой n-угольной пирамиды и принимается за развертку конуса. Ломаная линия, получающаяся на развертке пирамиды, заменяется плавной кривой, проходящей через те же точки. Чем большее число граней у вписанной пирамиды (не менее 8), тем меньше будет разница между действительной и приближенной разверткой конической поверхности.
Аналогичным образом развертка цилиндрической поверхности сводится к построению развертки n-гранной призмы.

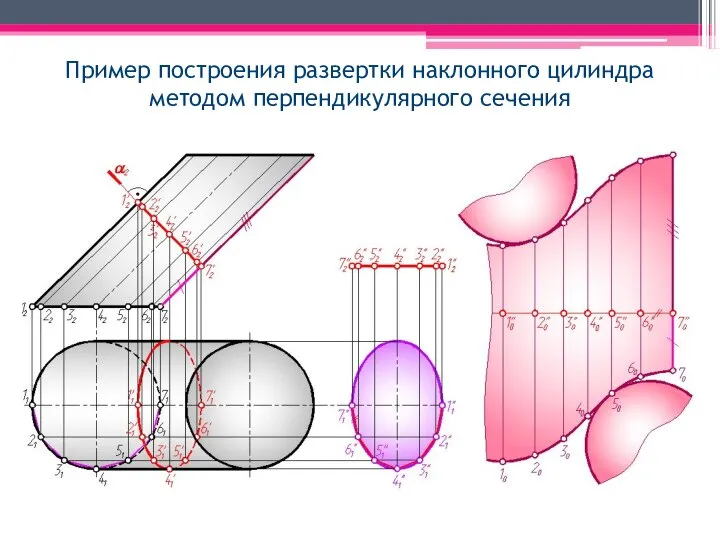
Пример построения развертки наклонного цилиндра методом перпендикулярного сечения

Уласевич З.Н., Уласевич В.П., Якубовская О.А. Начертательная геометрия в слайдах компьютерной среды Microsoft PowerPoint
Пример построения развертки
наклонного цилиндра
методом раскатки

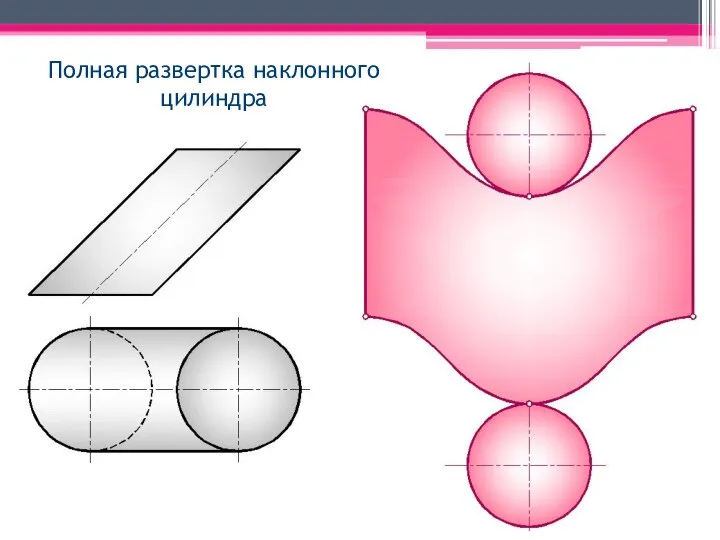
Полная развертка наклонного цилиндра

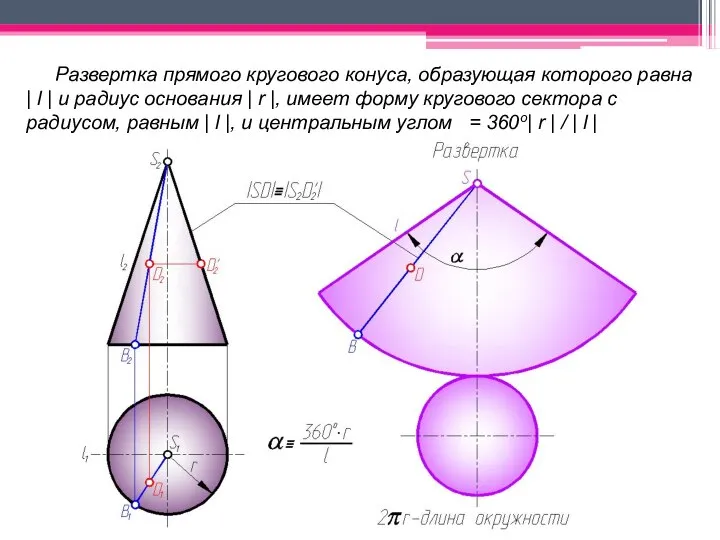
Развертка прямого кругового конуса, образующая которого равна | l | и радиус основания | r |, имеет форму кругового сектора с радиусом, равным | l |, и центральным углом = 360o| r | / | l |

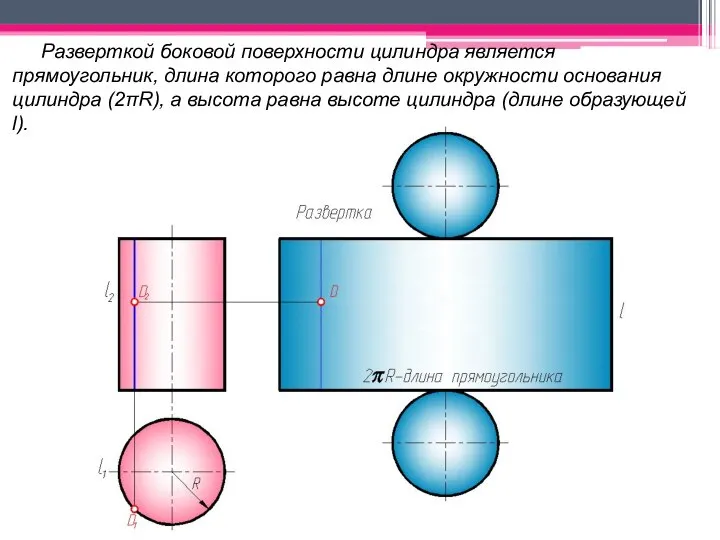
Разверткой боковой поверхности цилиндра является прямоугольник, длина которого равна длине окружности основания цилиндра (2πR), а высота равна высоте цилиндра (длине образующей l).

4. Построение условных разверток
неразвертывающихся поверхностей
Точную развертку неразвертывающейся поверхности построить нельзя. Для построения условной развертки такой поверхности применяют метод аппроксимации, который заключается в следующем.
Данная неразвертывающаяся поверхность разбивается на некоторые отсеки. Каждый из этих отсеков заменяется отсеком кривой развертывающейся поверхности.
При свертывании такой развертки, кроме изгибания, необходимо произвести частичное растяжение, или сжатие отдельных ее участков.