Razvitie_ponyatia_o_chisle_Tselye_i_ratsionalnye_chisla_Deystvitelnye_chisla

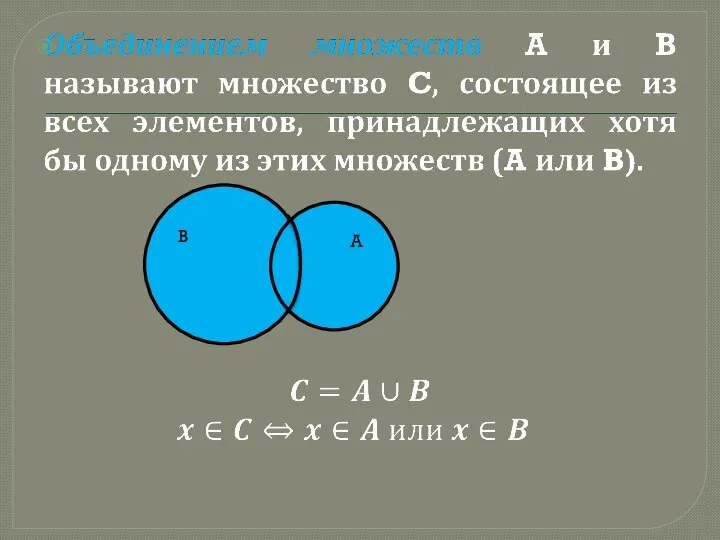
Понятие множества
Множество можно представить как совокупность некоторых объектов, объединенных по определенному признаку.

B
A

A
B
C

B
A

Целые и рациональные числа
В курсе математики чаще всего рассматриваются множества, элементами которых являются числа, и поэтому их называют числовыми множествами.

N
Z
Q

Иррациональные числа

Действительные числа
Рациональные и иррациональные числа образуют множество действительных чисел R.
Каждое действительное число может быть записано в виде бесконечной десятичной дроби: рациональные числа в виде бесконечной периодической десятичной дроби, а иррациональные- в виде бесконечной непериодической десятичной дроби.

Модуль действительного числа

0
b
a
B
O
A

Свойства модуля

Приближенные вычисления

Округление положительных десятичных дробей
Абсолютная погрешность, допускаемая при округлении, называется погрешностью округления.
Округление с недостатком до единиц некоторого разряда состоит в отбрасывании единиц всех младших разрядов.
Пример. Округлить с недостатком до сотых, десятых и
единиц число 54,376.
Решение. Имеем 54,37; 54,3; 54. Погрешности округлений
соответственно равны 0,006; 0,076; 0,376.
При округлении с избытком до единиц некоторого разряда число единиц данного разряда увеличивают на единицу.
Пример. Округлить с избытком до сотых, десятых и единиц
число 24,368.
Решение. Имеем 24,37; 24,4; 25. Погрешности округлений
соответственно равны 0,002; 0,032; 0,632.