Содержание
- 2. Рекурсия … послушать… «У попа была собака, Он ее любил. … посмотреть… встаньте между двумя зеркалами
- 3. Задачи с рекурсивной формулировкой Пример: вычисление факториала натурального числа Function factorial(n: integer): longint; Begin If n
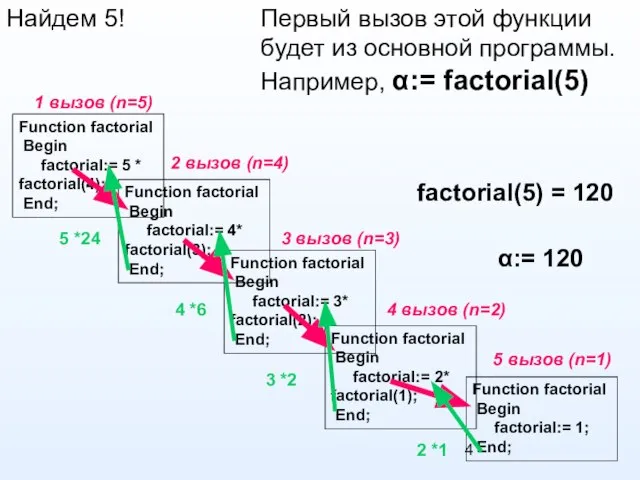
- 4. Найдем 5! Первый вызов этой функции будет из основной программы. Например, α:= factorial(5) Function factorial Begin
- 5. Задание Напишите рекурсивную программу определения суммы первых n натуральных чисел: Sn = Sn-1 + n; S1
- 6. Пример: перевод натурального числа из десятичной системы счисления в двоичную. 3910 = 1001112 Procedure Rec(n: integer);
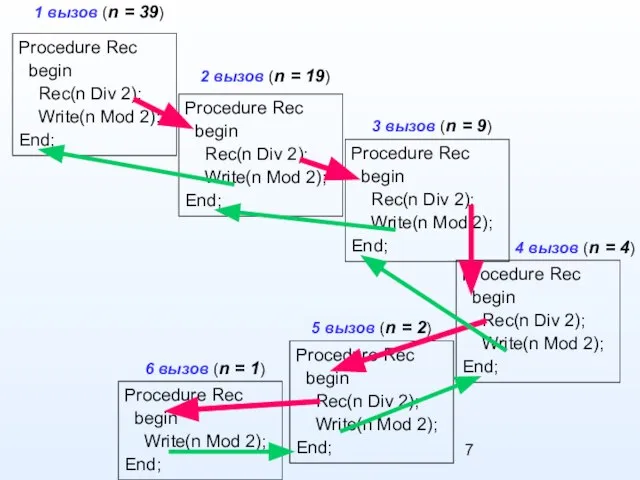
- 7. Procedure Rec begin Rec(n Div 2); Write(n Mod 2); End; 1 вызов (n = 39) Procedure
- 8. Задание Написать процедуру перевода числа из десятичной системы в N - ю, при условии, что 2
- 9. Напишите программу: Найти первые N чисел Фибоначчи. Каждое число равно сумме двух предыдущих чисел при условии,
- 10. Program chisla_Fibonachi; var i,n:integer; function fib(nf:integer):longint; begin if (nf=1) or (nf=2) then fib:=1 else fib:=fib(nf-1)+fib(nf-2); end;
- 11. Итерация повторное выполнение некоторых действий до тех пор, пока не будет удовлетворяться некоторое условие. Большинство алгоритмов
- 12. Выводит цифры целого положительного числа в обратном порядке Program Perevertish; Var n: longint; Procedure reverse(n: longint);
- 13. Число-полиндром - число, которое имеет тот же вид при прочтении его справа налево. Например: 121, 1230321,
- 14. Решение задач Даны первый член и разность арифметической прогрессии. Написать рекурсивную функцию для нахождения: a) n-го
- 15. 3. Написать рекурсивную функцию для вычисления: а) суммы цифр натурального числа; б) количества цифр натурального числа.
- 16. Procedure Picture1(x,y,r,r1,n:integer); Var x1,y1:integer; i:integer; Begin if n > 0 then {“заглушка”} begin circle(x,y,r);r1:=trunc(r*k2); {рисование окружности}
- 18. Скачать презентацию













 Реализация проекта «Лицейский технопарк» в рамках программы развития «МПЛ как инновационный образовательный центр».
Реализация проекта «Лицейский технопарк» в рамках программы развития «МПЛ как инновационный образовательный центр». Разработка стратегии развития предприятия сферы услуг
Разработка стратегии развития предприятия сферы услуг Жизнь в профессии Имидж учителя
Жизнь в профессии Имидж учителя Системы управления качеством
Системы управления качеством Подсистема памяти МПС
Подсистема памяти МПС Удержание ключевых сотрудников
Удержание ключевых сотрудников Информационная война. Распространение ложной информации
Информационная война. Распространение ложной информации Презентация на тему Мещерский край в географии и литературе
Презентация на тему Мещерский край в географии и литературе  Политика. Представления о политике. Политика как подсистема общества
Политика. Представления о политике. Политика как подсистема общества ОАО МРСК «Центра и Северного Кавказа»
ОАО МРСК «Центра и Северного Кавказа» Общие условия досудебного производства
Общие условия досудебного производства Некоммерческая организация «Ассоциация московских вузов»МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИРОССИЙСКОЙ ФЕДЕРАЦИИФЕДЕРАЛЬНОЕ АГЕ
Некоммерческая организация «Ассоциация московских вузов»МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИРОССИЙСКОЙ ФЕДЕРАЦИИФЕДЕРАЛЬНОЕ АГЕ Понедельник - день тяжелый?
Понедельник - день тяжелый? Управление воспитательным процессом
Управление воспитательным процессом Event менеджмент
Event менеджмент Космические аппараты на марках сразных стран
Космические аппараты на марках сразных стран Презентация на тему ЦАРСТВО ПРОКАРИОТЫ ПОДЦАРСТВО БАКТЕРИИ
Презентация на тему ЦАРСТВО ПРОКАРИОТЫ ПОДЦАРСТВО БАКТЕРИИ  Химия в криминалистике
Химия в криминалистике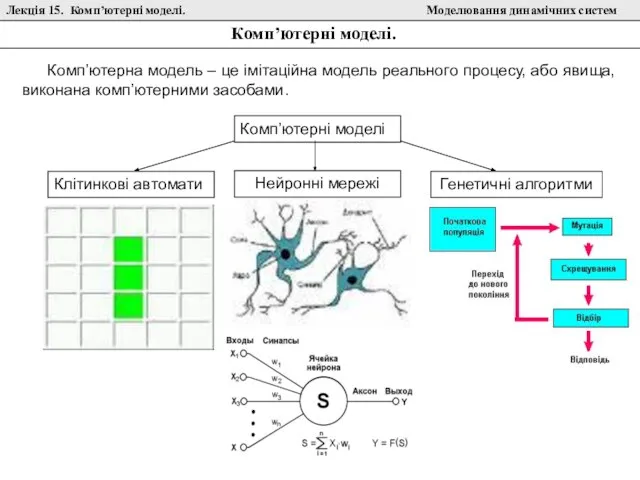 Клітинкові автомати
Клітинкові автомати Числовой луч (2 класс)
Числовой луч (2 класс) Адресаты лирики А.С. Пушкина.Женские портреты.
Адресаты лирики А.С. Пушкина.Женские портреты. Тема проекта:«Спортивные игры»
Тема проекта:«Спортивные игры» Проектирование информационных систем
Проектирование информационных систем Мое мировоззрение. Мое отношение к религии
Мое мировоззрение. Мое отношение к религии НОВЫЕ ТЕХНОЛОГИИ на рынке ГКО-ОФЗ на ММВБ
НОВЫЕ ТЕХНОЛОГИИ на рынке ГКО-ОФЗ на ММВБ 14 марта – День православной книги
14 марта – День православной книги Інформаційна система та її складові
Інформаційна система та її складові Доклад«Теоретические аспекты информационного поиска»
Доклад«Теоретические аспекты информационного поиска»