Решение краевых задач ОДУ

История дифферинциальных исчислений
17 в.
И. Ньютон и Г. Лейбниц,
братья Я. и И. Бернулли, Б. Тейлор
18 в.
Л. Эйлер и Ж. Лагранж
19 в.
Коши, Б. Больцан и К. Гаус

Основные понятия
Дифференциальным уравнением называется уравнение, связывающее не­зависимую переменную неизвестную функцию x(t) этой независимой пере­меной и ее производные
Краевые задачи, задачи, в которых из некоторого класса функций, определённых в данной области, требуется найти ту, которая удовлетворяет на границе (крае) этой области заданным условиям

Золотое сечение
Метод золотого сечения — метод поиска значений действительно - значной функции на заданном отрезке. В основе метода лежит принцип деления в пропорциях золотого сечения. Наиболее широко известен как метод поиска экстремума в решении задач оптимизации.

Формализация
Шаг 1. Задаются начальные границы отрезка и точность ε,
рассчитывают начальные точки деления:
Шаг 2.
Если
то
Иначе
Шаг 3.
Если
, то
и останов.
Иначе возврат к шагу 2.

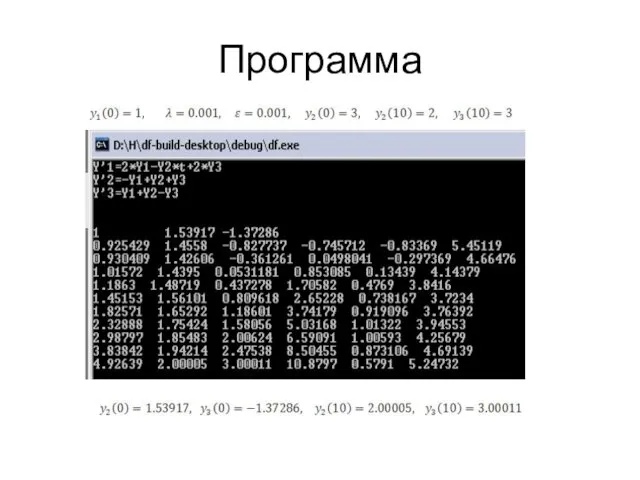
Программа

Градиентный метод
Градиентный спуск — метод нахождения локального минимума (максимума) функции с помощью движения вдоль градиента. Для минимизации функции в направлении градиента используются методы одномерной оптимизации, например, метод золотого сечения

Алгоритм
1.Задают начальное приближение и точность расчёта
2.Рассчитывают , где
3.Проверяют условие остановки:
Если , то и переход к шагу 2.
Иначе и останов.
,
,

Программа