Слайд 2Однородная линия без потерь при гармонических напряжениях и токах

Слайд 3Линией без потерь считается линия, у которой R0 << ωL0 и G0

<< ωC0 , поэтому R0 ≈ 0, G0 ≈ 0
Слайд 6Амплитуды падающей и отраженной волн напряжения и тока вдоль линии меняться не

будут (α = 0)
Слайд 7Будет изменяться фаза напряжения и тока вдоль линии (β ≠ 0)

Слайд 8Поскольку α и v не зависят от ω, то линия без потерь

является линией без искажений
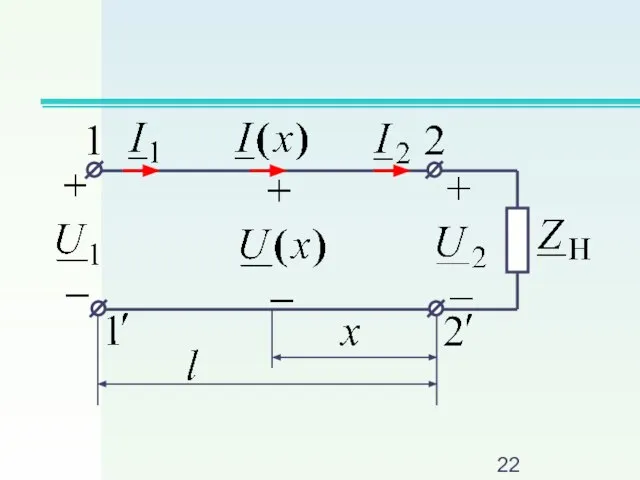
Слайд 10Тогда основные уравнения однородной линии без потерь при отсчете x от конца

линии будут следующими
Слайд 1214 лекция
Однородная линия без потерь при гармонических напряжениях и токах

Слайд 13Если и
, то мгновенные значения будут следующими

Слайд 16Для любого момента времени распределение напряжения и тока вдоль линии в функции

x является гармоническим
Слайд 19Комплекс входного
сопротивления линии
где - сопротивление
нагрузки

Слайд 20Режимы однородной линии без потерь

Слайд 21Проанализируем для комплексов действующих значений напряжений и токов с использованием основных уравнений

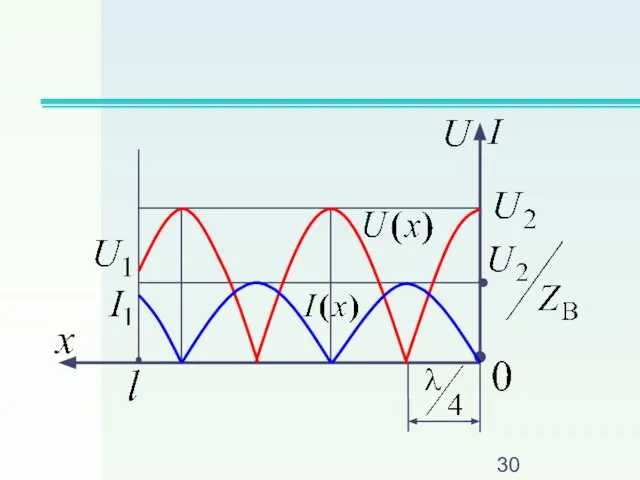
Слайд 231. Режим холостого хода, когда ZН =∞ и I2 = 0

Слайд 25В линии стоячие волны напряжения и тока

Слайд 26Стоячие волны – это результат наложения падающих и отраженных волн с одинаковой

амплитудой
Слайд 27При стоячих волнах активная мощность в любой точке линии равна нулю

Слайд 28При стоячих волнах пучности и узлы неподвижны и сдвинуты друг относительно друга

на
Слайд 29Построим графики для действующих значений

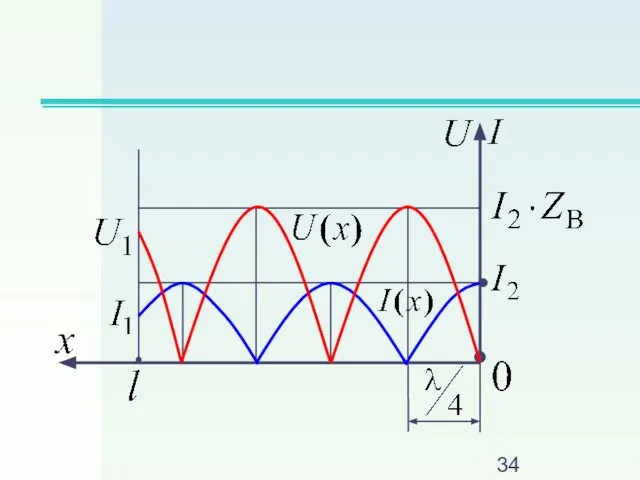
Слайд 312. Режим короткого замыкания, когда ZН = 0 и U2 = 0

Слайд 33В линии – стоячие волны
Действующие значения:

Слайд 353. Режим реактивной нагрузки, когда ZН = j⋅XH ,
U2 = j⋅XH⋅I2

,
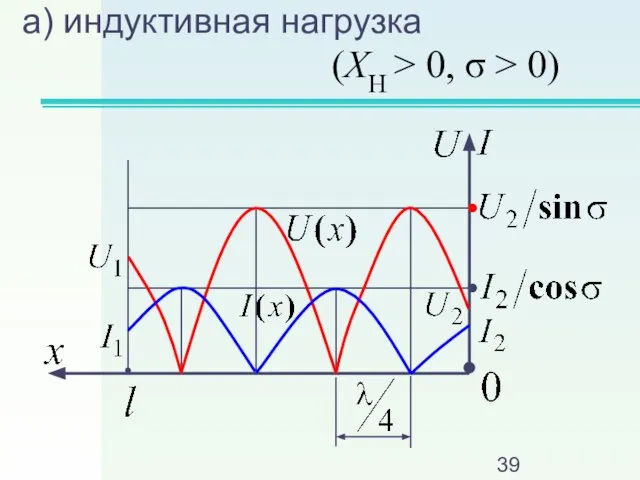
Слайд 38В линии – стоячие волны
Действующие значения:

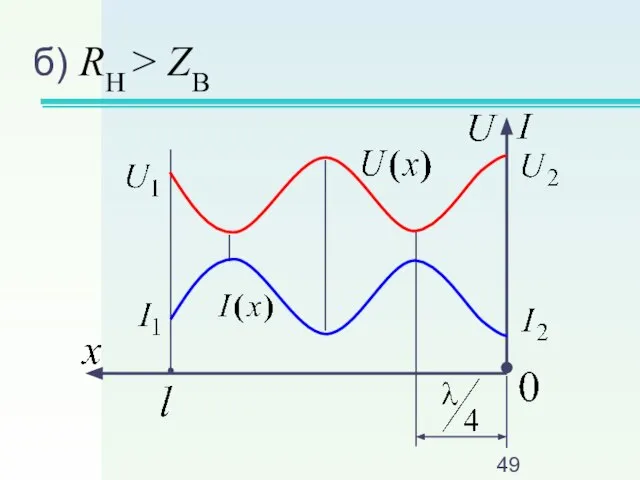
Слайд 39а) индуктивная нагрузка
(XH > 0, σ > 0)
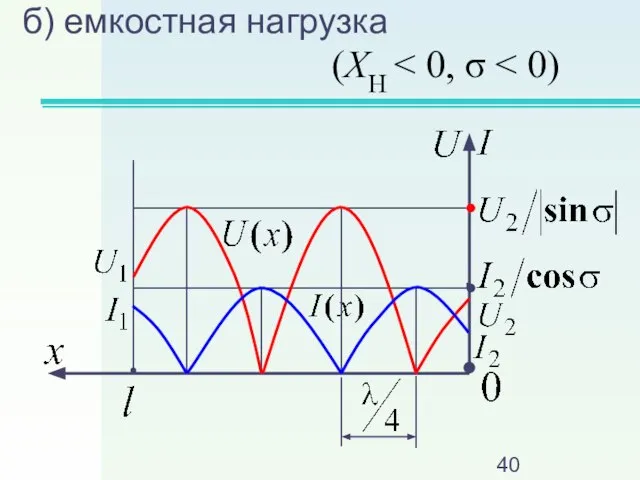
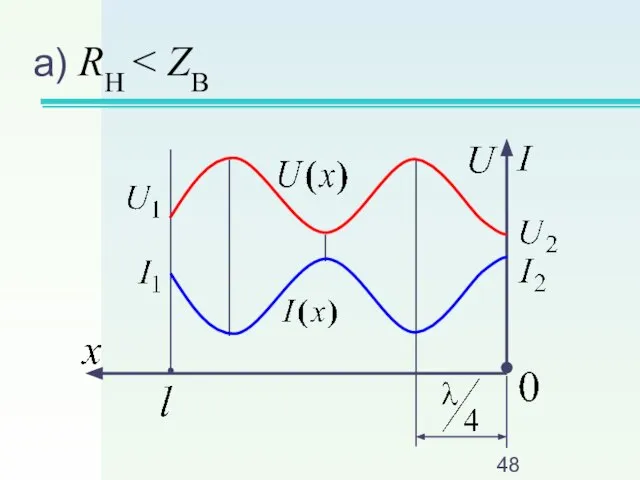
Слайд 40б) емкостная нагрузка
(XH < 0, σ < 0)
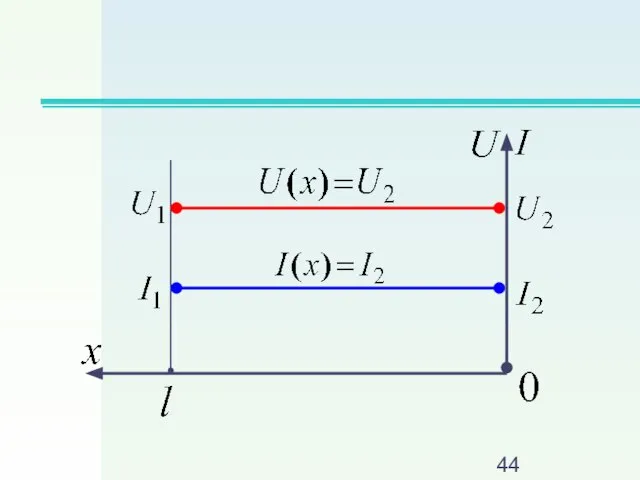
Слайд 414. Режим согласованной нагрузки, когда

Слайд 43Стоячих волн нет
Действующие значения:

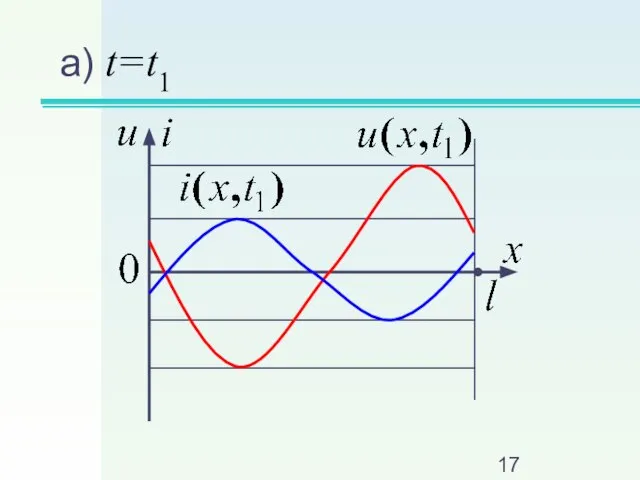
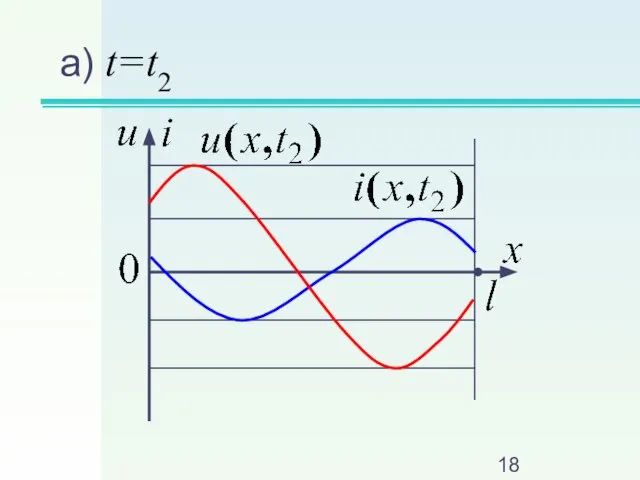
Слайд 455. Режим активной нагрузки, когда

Слайд 47Стоячих волн нет
Действующие значения:




















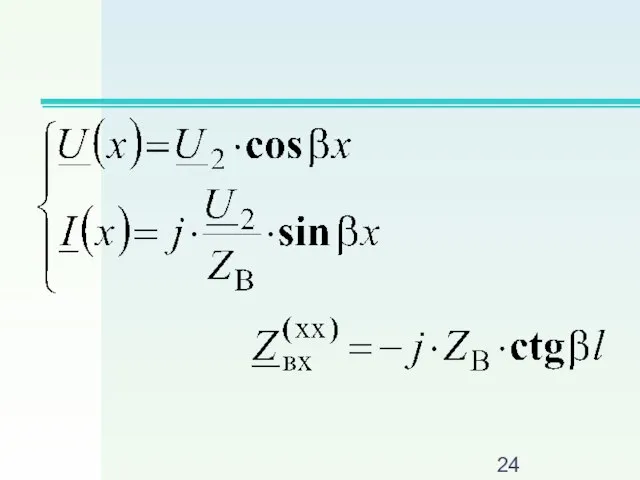




















 Football
Football Презентация на тему Травмы глаз
Презентация на тему Травмы глаз  Презентация «Гринпис. Цифры и факты» может использоваться при изучении тем «Давайте заботиться о нашей Планете Земля !»( 7класс И. Л
Презентация «Гринпис. Цифры и факты» может использоваться при изучении тем «Давайте заботиться о нашей Планете Земля !»( 7класс И. Л Содоклад заместителя председателя Правительства Пермского края Цветова В.Ю. «Об итогах социально-экономического развития Суксун
Содоклад заместителя председателя Правительства Пермского края Цветова В.Ю. «Об итогах социально-экономического развития Суксун Понятие о систематике растений
Понятие о систематике растений Корпус общественных наблюдателей
Корпус общественных наблюдателей Пакет «Имплантация зубов»
Пакет «Имплантация зубов» BitcoinQ. Помочь людям стать финансово свободными. Гармонизировать все сферы жизни
BitcoinQ. Помочь людям стать финансово свободными. Гармонизировать все сферы жизни Формирование клиентооринтированного поведения ППВ
Формирование клиентооринтированного поведения ППВ Комплектование архива документами архивного фонда РФ и другими архивными документами
Комплектование архива документами архивного фонда РФ и другими архивными документами Интеллектуальные собственные нужды Производственная компания «Электроконцепт» Вячеслав Шеин, генеральный директор 2-я междуна
Интеллектуальные собственные нужды Производственная компания «Электроконцепт» Вячеслав Шеин, генеральный директор 2-я междуна Презентация на тему Романская и Готическая архитектура Основные отличия 6 класс
Презентация на тему Романская и Готическая архитектура Основные отличия 6 класс  Действующая нормативная и техническая документация в отрасли общественного питания
Действующая нормативная и техническая документация в отрасли общественного питания Заочная экскурсия в Мордовский республиканский музей им. С. Д. Эрьзи
Заочная экскурсия в Мордовский республиканский музей им. С. Д. Эрьзи Рассказы о геометрии
Рассказы о геометрии Роспись по стеклу
Роспись по стеклу Организация внеурочной деятельности в условиях введения ФГОСобщего образования
Организация внеурочной деятельности в условиях введения ФГОСобщего образования С.Ю. Глазьев О стратегии экономического развития России
С.Ю. Глазьев О стратегии экономического развития России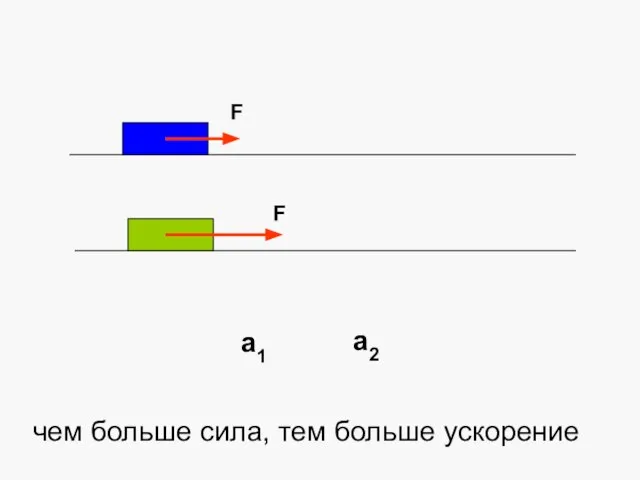 а1
а1 Основы поддержания жизни и автоматическая наружная дефибрилляция
Основы поддержания жизни и автоматическая наружная дефибрилляция  Создание и продвижение промо видео, реклама, анимация, корпоративные фильмы. Er-production.ru медиа студия
Создание и продвижение промо видео, реклама, анимация, корпоративные фильмы. Er-production.ru медиа студия Металлы
Металлы Заказники и национальные парки
Заказники и национальные парки Устройства преобразования электрической энергии: назначение, классификация, структурные схемы. (Лекция 8)
Устройства преобразования электрической энергии: назначение, классификация, структурные схемы. (Лекция 8) Контрольные вопросы Какие из приведенных соединений относятся к органическим? Ответ 1 : все приведенные соединения Ответ 2 : б, в, г,
Контрольные вопросы Какие из приведенных соединений относятся к органическим? Ответ 1 : все приведенные соединения Ответ 2 : б, в, г,  Лицензирование и его роль
Лицензирование и его роль О КОНСОЛИДАЦИИ АВИАПРЕДПРИЯТИЙ ДАЛЬНЕГО ВОСТОКА
О КОНСОЛИДАЦИИ АВИАПРЕДПРИЯТИЙ ДАЛЬНЕГО ВОСТОКА Первобытные охотники и собиратели
Первобытные охотники и собиратели