Слайд 2Построить область решений
системы неравенств
Выполним построение в программе GeoGebra
В командной строке наберем
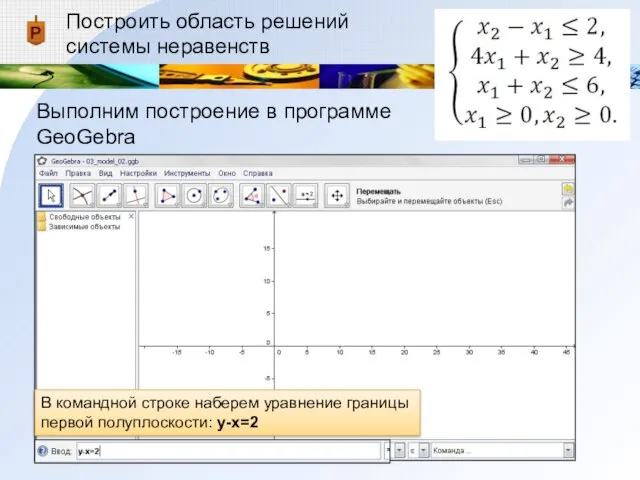
уравнение границы первой полуплоскости: y-x=2
Слайд 3Построить область решений
системы неравенств
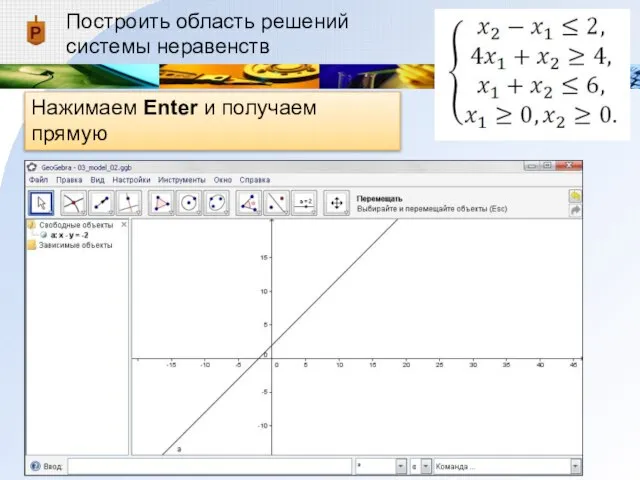
Нажимаем Enter и получаем прямую
Слайд 4Построить область решений
системы неравенств
Подставим в неравенство начало координат А(0;0): 0-0<2 –
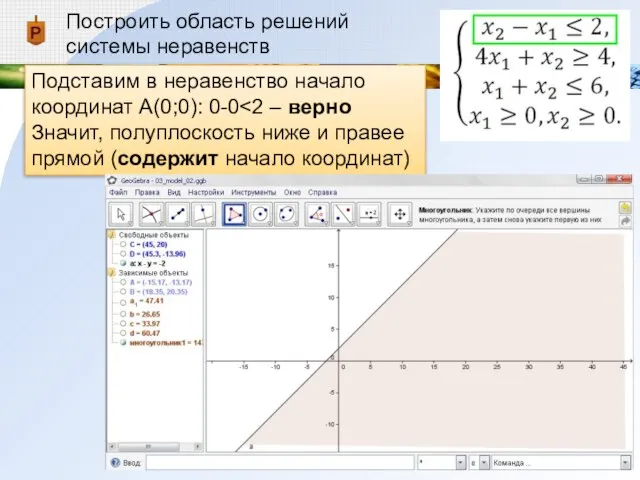
верно
Значит, полуплоскость ниже и правее прямой (содержит начало координат)
Слайд 5Замечание:
С помощью инструмента Многоугольник выполнили вспомогательное построение – изобразили заливкой полуплоскость.
Не
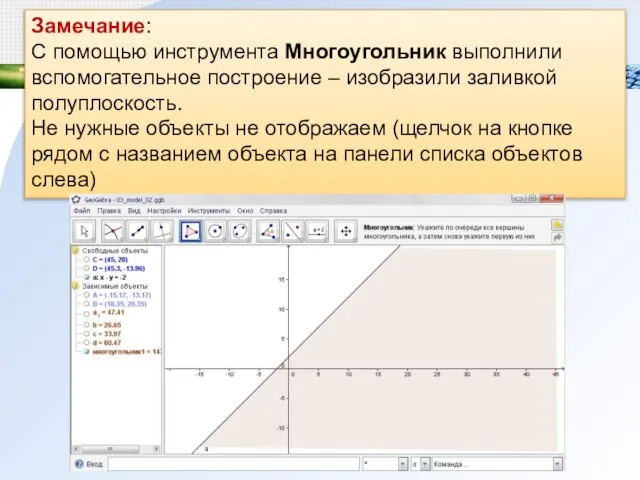
нужные объекты не отображаем (щелчок на кнопке рядом с названием объекта на панели списка объектов слева)
Слайд 6Замечание:
Чтобы удалить вспомогательные объекты, выполняем правый щелчок по названию объекта в списке
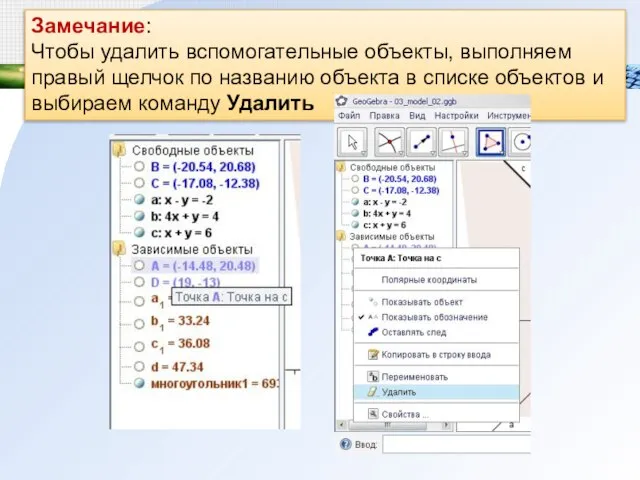
объектов и выбираем команду Удалить
Слайд 7Построить область решений
системы неравенств
Построим вторую полуплоскость
Построим прямую – границу полуплоскости (в
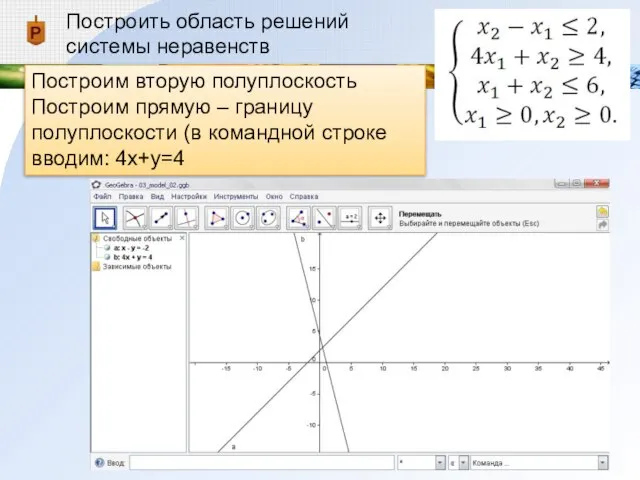
командной строке вводим: 4x+y=4
Слайд 8Построить область решений
системы неравенств
Подставим в неравенство координаты А(0;0): 4*0+0>4 – не
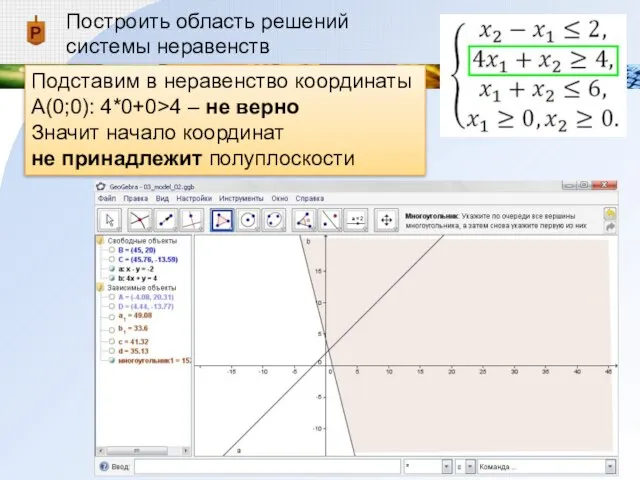
верно
Значит начало координат
не принадлежит полуплоскости
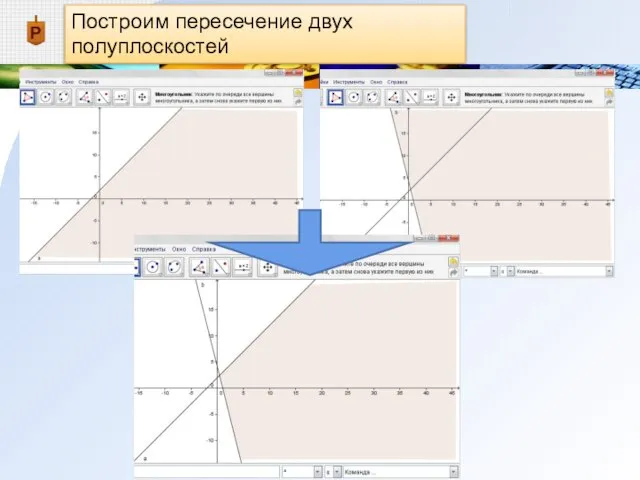
Слайд 9Построим пересечение двух полуплоскостей
Слайд 10Построить область решений
системы неравенств
Построим третью полуплоскость
Построим прямую – границу полуплоскости (в
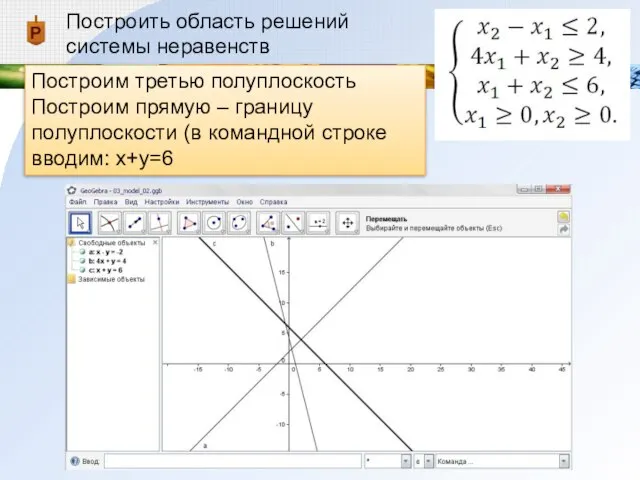
командной строке вводим: x+y=6
Слайд 11Построить область решений
системы неравенств
Подставим в неравенство координаты А(0;0): 0+0<6 – верно
Значит
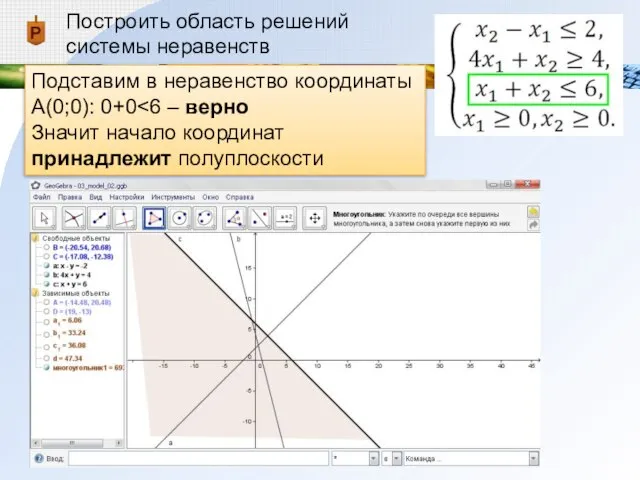
начало координат принадлежит полуплоскости
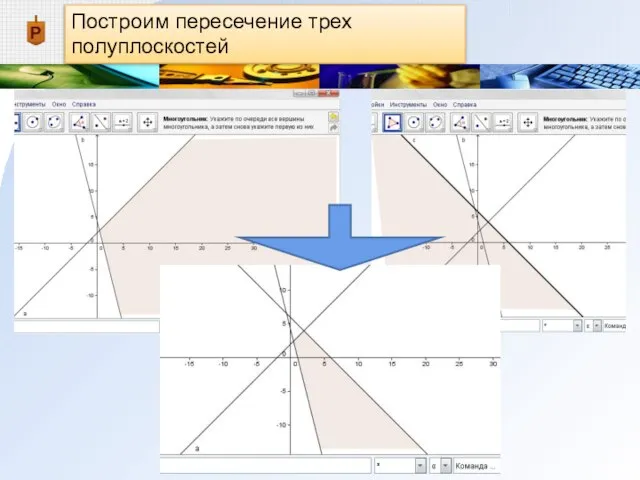
Слайд 12Построим пересечение трех полуплоскостей
Слайд 13Построить область решений
системы неравенств
Оставшиеся ограничения
(условие неотрицательности переменных) задают первую координатную четверть
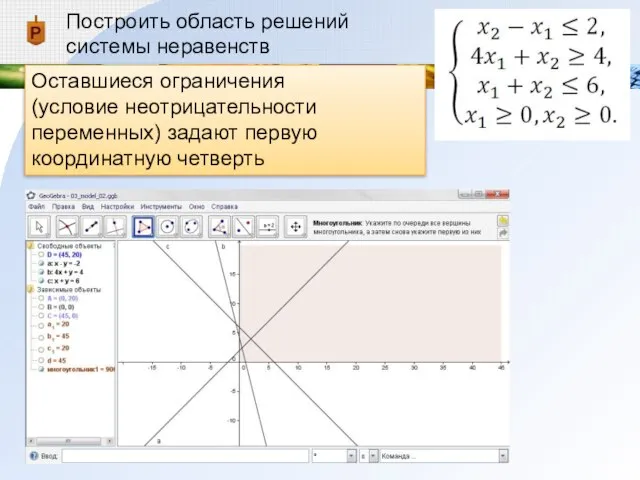
Слайд 14Построим пересечение всех полуплоскостей
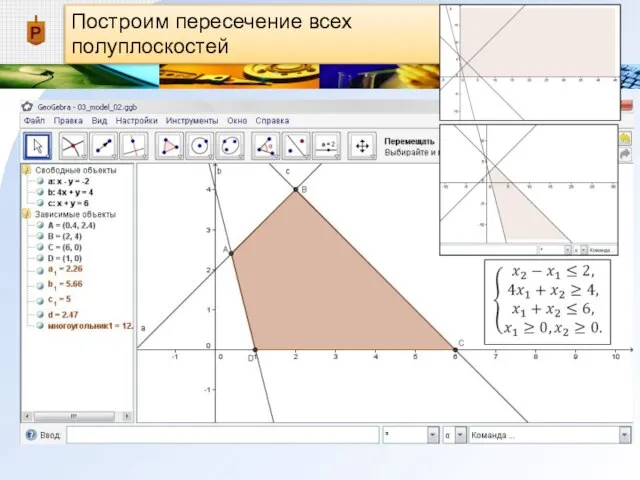
Слайд 15Замечание
С помощью инструмента Пересечение двух объектов строим точки пересечения всех прямых:
Выбрав инструмент

выполняем последовательно щелчок по одной прямой и по другой прямой
Слайд 16Замечание
С помощью инструмента Многоугольник строим замкнутую область – решение системы неравенств:
Выбрав инструмент
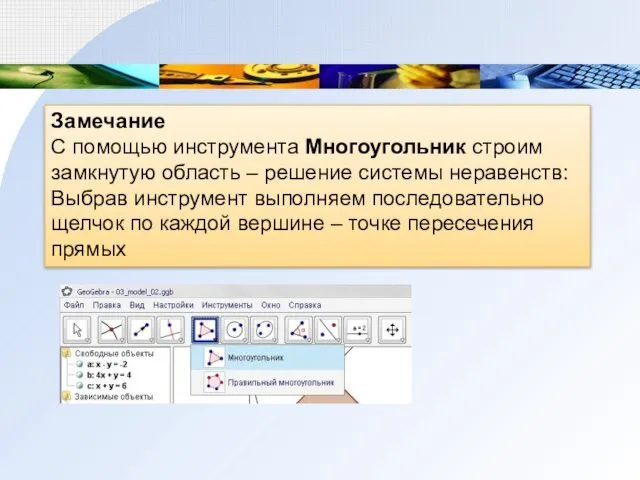
выполняем последовательно щелчок по каждой вершине – точке пересечения прямых















 Программный комплекс «МагПро КриптоПортал»
Программный комплекс «МагПро КриптоПортал» Ракообразные
Ракообразные Из опыта работы по проблемно-диалоговому обучению физике
Из опыта работы по проблемно-диалоговому обучению физике Город Ангелов
Город Ангелов  Ремонтная программа на 2021 год. Котельный цех
Ремонтная программа на 2021 год. Котельный цех Центр социологических исследований РГГУ
Центр социологических исследований РГГУ Практикум1
Практикум1 Кейс. Мультиязычное продвижение сайтаотеля под Google
Кейс. Мультиязычное продвижение сайтаотеля под Google Ак-барс. Изображение барса в скульптуре
Ак-барс. Изображение барса в скульптуре Типы связей и системы управления
Типы связей и системы управления Презентация на тему Волшебник изумрудного города
Презентация на тему Волшебник изумрудного города Презентация на тему Правила поведения с друзьями и родственниками
Презентация на тему Правила поведения с друзьями и родственниками Тема: Изображение на физических картах высот и глубин. Значение планов и карт.
Тема: Изображение на физических картах высот и глубин. Значение планов и карт. Виды рефлексии в психологии
Виды рефлексии в психологии Региональный Центр персонализации универсальных электронных карт (УЭК). Типовые решения.
Региональный Центр персонализации универсальных электронных карт (УЭК). Типовые решения. Технологический Институт Пищевой Промышленности
Технологический Институт Пищевой Промышленности Прыжок в длину с места учет
Прыжок в длину с места учет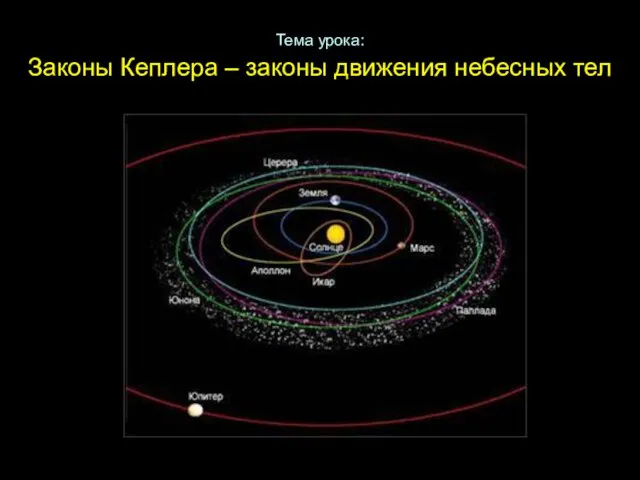 Тема урока: Законы Кеплера – законы движения небесных тел
Тема урока: Законы Кеплера – законы движения небесных тел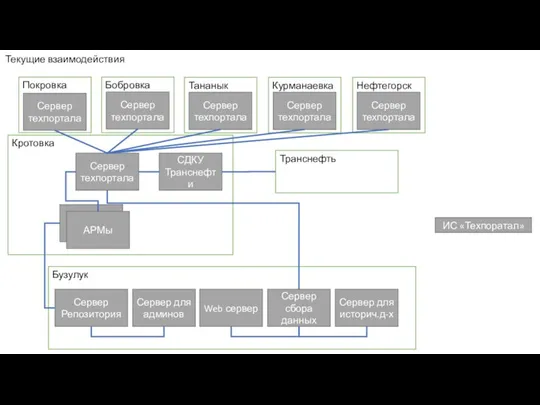 Схематичная схема Транснефть и Бузулук
Схематичная схема Транснефть и Бузулук Презентация по английскому Сергей Александрович Есенин
Презентация по английскому Сергей Александрович Есенин  Курсовая работа. Шаблон
Курсовая работа. Шаблон Как решать кейсы
Как решать кейсы Презентация на тему Правописание предлогов
Презентация на тему Правописание предлогов Classical Theories of International Trade
Classical Theories of International Trade  Комплексная работапо внедрению автоматизированных систем в управление школой
Комплексная работапо внедрению автоматизированных систем в управление школой Религиозные представления народов Северной Европы.
Религиозные представления народов Северной Европы. Справедливая стоимостьв МСФО
Справедливая стоимостьв МСФО Волейбол
Волейбол