Слайд 2План:
1) Квадратные уравнения.
2) Теорема Виета.
3) Из истории.
4) Формула Кардано.
5) Метод Феррари.

Слайд 3Решение уравнений II,III,IV-й степеней по формуле.
Уравнения первой степени, т.е. линейные, нас

учат решать ещё с первого класса, и особого интереса к ним не проявляют. Интересны нелинейные уравнения т.е. больших степеней. Среди нелинейных ( уравнений общего вида, не решающихся разложением на множители или каким-либо другим относительно простым способом ) уравнения низших степеней (2,3,4-й) можно решить с помощью формул. Уравнения 5-й степени и выше неразрешимы в радикалах (нет формулы). Поэтому мы рассмотрим только три метода.
Слайд 4 I. Квадратные уравнения.
Формула Виета.
Дискриминант квадратного трехчлена.
Для любого приведённого кв.

уравнения справедлива формула :
Обозначим: D=p-4q тогда формула примет вид:
Выражение D называют дискриминантом. При исследовании кв. трехчлена смотрят на знак D. Если D>0,то корней 2; D=0, то корень 1; если D<0, то корней нет.
Слайд 5II. Теорема Виета
Для любого приведённого кв. уравнения
Справедлива теорема Виета:
Для любого уравнения n-ой

степени теорема Виета также справедлива: коэффициент взятый с противоположным знаком, равен сумме его n корней; свободный член равен произведению n его корней и числа (-1) в n степени.
Слайд 6Вывод формулы Виета.
Запишем формулу квадрата суммы
И заменим в ней a на

х, b на
Получим:
Теперь отсюда вычтем первоначальное равенство:
Теперь нетрудно получить нужную формулу.
Слайд 8III. Из истории.
В XV-XVI вв. расцвет науки происходит главным образом в Италии,

во Франции и в Германии, а позднее, - в конце 16 в., - в Голландии, которая в это время переживала первую в Европе буржуазную революцию.
Слайд 9Итальянские математики 16 в. сделали крупнейшее математическое открытие. Они нашли формулы для

решения уравнений третьей и четвертой степеней.
Рассмотрим произвольное кубическое уравнение:
И покажем, что с помощью подстановки его можно преобразить к виду
Пусть Получим:
Положим т.е. Тогда данное уравнение
примет вид
Слайд 10В 16 в. было распространено соревнование между учеными, проводившееся в форме диспута.

Математики предлагали друг другу определенное число задач, которые нужно было решить к началу поединка. Выигрывал тот, кто решил большее число задач.
Антонио Фиоре постоянно участвовал в турнирах и всегда выигрывал, так как владел формулой для решения кубических уравнений. Победитель получал денежное вознаграждение, ему предлагали почетные, высоко оплачиваемые должности.
Слайд 11IV. Тарталья преподавал математику в Вероне, Венеции, Брешии. Перед турниром с Фиоре

он получил от противника 30 задач, увидев,что все они сводятся к кубическому уравнению
И приложил все силы для его решения. Отыскав формулу, Тарталья решил все задачи, преложенные ему Фиоре, и выиграл турнир. Через день после поединка он нашел формулу для решения уравнения
Это было величайшее открытие. После того как в Древнем Вавилоне была найдена формула для решения квадратных равнений, выдающиеся математики в течение двух тысячелетий безуспешно пытались найти формулу для решений кубических уравнений. Метод решения Тарталья держал втайне.
Рассмотрим уравнение
Тарталья использовал подстановку
Слайд 12Из уравнения он получил:
Для u и v получена система
Значит, они являются

корнями квадратного уравнения
Следовательно, для отыскания х имеем формулу
Слайд 13Ее называют сейчас формулой Кардано, так как она впервые была опубликована в

1545 г. в книге Кардано «Великое искусство, или Об алгебраических правилах».
Джироламо Кардано (1501-1576) окончил университет в Падуе. Его главным занятием была медицина. Кроме того, он занимался философией, математикой, астрологией, составлял гороскопы Петрарки, Лютера, Христа, английского короля Эдуарда 6. Папа римский пользовался услугами Кардано - астролога и покровительствовал ему. Кардано умер в Риме. Существует легенда, что он покончил жизнь самоубийством в тот день, который предсказал, составляя собственный гороскоп, как день своей смерти.
Слайд 14Кардано неоднократно обращался к Тарталье с просьбой сообщить ему формулу для решения

кубических уравнений и обещал хранить ее тайну. Он не сдержал слова и опубликовал формулу, указав, что Тарталье принадлежит честь открытия «такого прекрасного и удивительного, превосходящего все таланты человеческого духа».
В книге Кардано «Великое искусство…» опубликована также формула для решения уравнений четвертой степени, которую открыл Луиджи Феррари (1522-1565)-ученик Кардано, его секретарь и поверенный.
Слайд 15V. Изложим метод Феррари. Запишем общее уравнение четвертой степени:
С помощью подстановки его

можно привести к виду
Используя метод дополнения до полного квадрата, запишем:
Феррари ввел параметр и получил:
Отсюда
Учитывая, получим
В левой части уравнения стоит полный квадрат, а в правой - квадратный трехчлен относительно х. Чтобы правая часть была полным квадратом, необходимо и достаточно, чтобы дискриминант квадратного трехчлена равнялся нулю, т.е. число t должно удовлетворять уравнению
Слайд 16
Кубические уравнения Феррари решил по формуле Кардано. Пусть - корень уравнения. Тогда

уравнение запишется в виде
Отсюда получаем два квадратных уравнения:
Они дают четыре корня исходного уравнения.
Слайд 17Приведем пример. Рассмотрим уравнение
Легко проверить, что -корень этого уравнения.
Естественно считать, что, используя

формулу Кардано, мы найдем этот корень. Проведем вычисления, учитывая, что
По формуле находим:
Как понять выражение На этот вопрос первым ответил инженер Рафаэль Бомбелли (ок. 1526-1573), работавший в Болонье В 1572 г. он издал книгу «Алгебра», в которую ввел в математику число i, такое, что
Бомбелли сформулировал правила операций с числом
Согласно теории Бомбелли,выражение можно записать так:
А корень уравнения, имеющий вид, можно записать так:
Слайд 18Вывод:
Изучая данную тему, я пришёл к выводу,
что существуют

формулы для решения уравнений II, III, IV степеней, не входящие в школьный курс математики. Корни уравнения не всегда действительные числа.

















 Презентация на тему Герои-космонавты
Презентация на тему Герои-космонавты Презентация без названия
Презентация без названия Храм в честь Всех Святых
Храм в честь Всех Святых Деньги. Игра Верю – не верю
Деньги. Игра Верю – не верю Российский экономический менталитет.
Российский экономический менталитет. Стрелочные переводы
Стрелочные переводы Работа электрического тока 8 класс
Работа электрического тока 8 класс Виды и формы корпоративной литературы
Виды и формы корпоративной литературы Город, где живут морфемы
Город, где живут морфемы Бизнес-планирование и эффективная презентация
Бизнес-планирование и эффективная презентация Летучка по теме : Меры уголовно-процессуального принуждения Подготовила: Калужина Ю.К.
Летучка по теме : Меры уголовно-процессуального принуждения Подготовила: Калужина Ю.К. The difference between dc and ac generators
The difference between dc and ac generators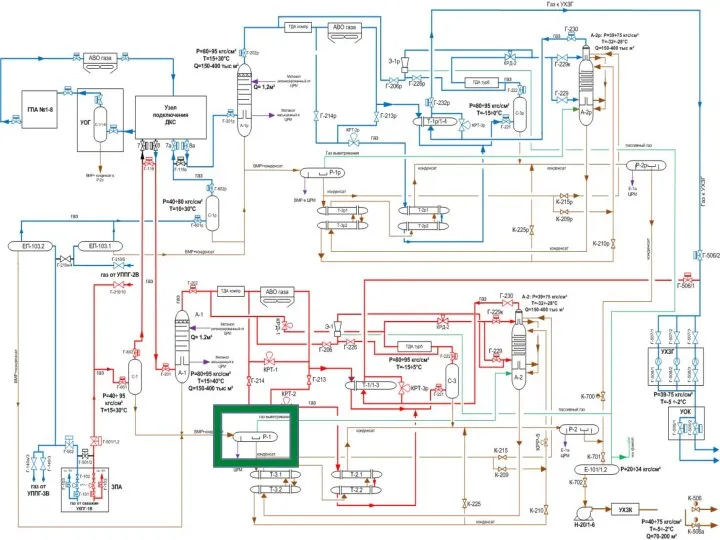 УК Проммаштехнология
УК Проммаштехнология Расчет тепловых процессов топки котла
Расчет тепловых процессов топки котла Правовые основы использования долин малых рек
Правовые основы использования долин малых рек ФСБУ 25 Применение. На что обратить внимание
ФСБУ 25 Применение. На что обратить внимание Убеждающая коммуникация
Убеждающая коммуникация Публичный доклад администрацииМуниципального бюджетного общеобразовательного учреждения«Средней общеобразовательной школы
Публичный доклад администрацииМуниципального бюджетного общеобразовательного учреждения«Средней общеобразовательной школы DexSys IT компания г. Ижевска
DexSys IT компания г. Ижевска Содержание предмета "Технология" с точки зрения нового образовательного стандарта
Содержание предмета "Технология" с точки зрения нового образовательного стандарта People
People Вечер памяти Александра Вампилова
Вечер памяти Александра Вампилова Путешествия. Карелия. Май 2017
Путешествия. Карелия. Май 2017 Системы автоматизации и телеметрии газорегуляторных пунктов. Внедрение типовых технических решений в ГРС
Системы автоматизации и телеметрии газорегуляторных пунктов. Внедрение типовых технических решений в ГРС Импульс. Завод нефтегазового оборудования
Импульс. Завод нефтегазового оборудования Нефть США
Нефть США Война в изображении Л. Н. Толстого
Война в изображении Л. Н. Толстого Реконкиста. Образование централизованных государств на Пиренеях
Реконкиста. Образование централизованных государств на Пиренеях