Системы счисления 11 класс

Система исчисления

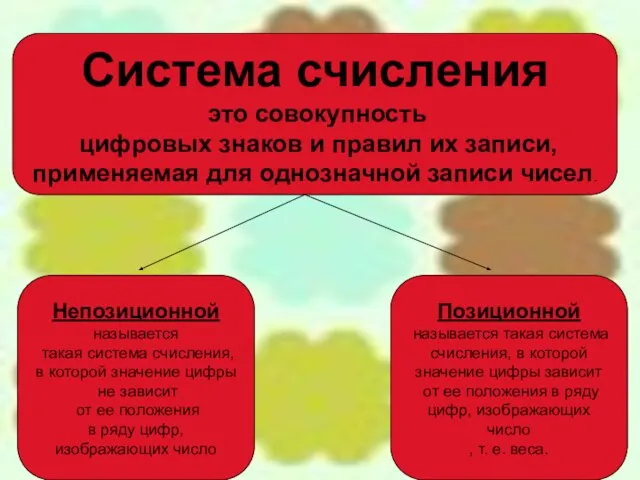
Система счисления
это совокупность
цифровых знаков и правил их записи,
применяемая для однозначной записи чисел.
Непозиционной
называется
такая система счисления,
в которой значение цифры
не зависит
от ее положения
в ряду цифр,
изображающих число
Позиционной
называется такая система
счисления, в которой
значение цифры зависит
от ее положения в ряду
цифр, изображающих число
, т. е. веса.

Позиционная система счисления
«Вавилонская» или шестидесятеричная система счисления;
Десятичная система счисления
Двоичная система счисления
Восьмеричная система счисления
Шестнадцатеричная система счисления

Вавилонская или шестидесятеричная система счисления
Шестидесятеричная вавилонская система — первая известная нам система счисления, основанная на позиционном принципе. Система вавилонян сыграла большую роль в развитии математики и астрономии, ее следы сохранились до наших дней. Так, мы до сих пор делим час на 60 минут, а минуту на 60 секунд. Точно так же, следуя примеру вавилонян, окружность мы делим на 360 частей (градусов). В ходе своего развития человечество стремилось совершенствовать запись чисел, у разных народов в разное время потреблялись различные системы счисления.

Десятичная система счисления
Пришла в Европу из Индии, где она появилась не позднее VI века н.э. В этой системе 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). В десятичной системе счисления особую роль играют число 10 и его степени: 10, 100, 1000 и т.д. Самая правая цифра числа показывает число единиц, вторая справа - число десятков, следующая - число сотен и т.д.
55510= 5*100 + 5*10 + 5*1

Двоичная система счисления была придумана математиками и философами ещё до появления компьютеров (XVII — XIX вв.). Выдающийся математик Лейбниц говорил: "Вычисление с помощью двоек... является для науки основным и порождает новые открытия... При сведении чисел к простейшим началам, каковы 0 и 1, везде появляется чудесный порядок". Позже двоичная система была забыта, и только в 1936 — 1938 годах американский инженер и математик Клод Шеннон нашёл замечательные применения двоичной системы при конструировании электронных схем.
Двоичная система счисления

2000
2000:2=1000(0 - остаток),
1000:2=500(0),
500:2=250(0),
250:2=125(0),
125:2=62(1),
62:2=31(0),
31:2=15(1),
15:2=7(1),
7:2=3(1),
3:2=1(1)
200010=11110100002

В этой системе счисления 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, указанная в самом младшем разряде, означает - как и в десятичном числе - просто единицу.
Восьмеричная система счисления

Данной системе счисления используется 16 цифр. Однако в десятичной системе использовали только 10 цифр. Поэтому возникла необходимость ввести новые цифры. В качестве этих цифр были выбраны латинские буквы A, B, C, D, E, F. То есть в 16-ричной системе счисления используют числа 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. При этом A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Шестнадцатеричная система счисления

Правила перевода

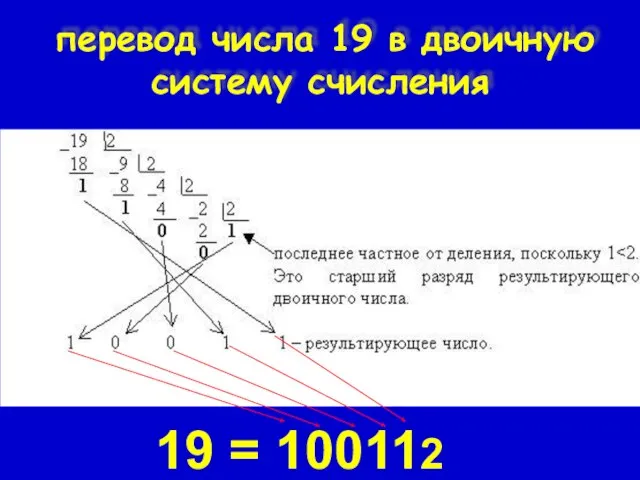
перевод числа 19 в двоичную систему счисления
19 = 100112

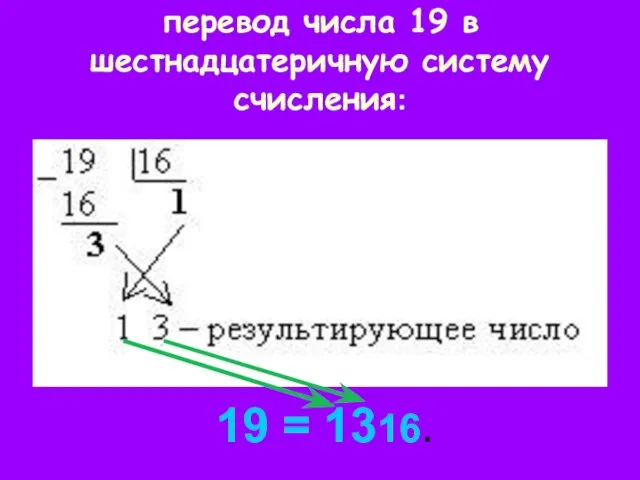
перевод числа 19 в шестнадцатеричную систему счисления:
19 = 1316.

перевод числа 1316 в десятичную систему счисления.
1316 = 1*16 + 3*16 = 16 + 3 = 19
1316 = 1910
перевод числа 100112 в десятичную
систему счисления.
100112 = 1*24 + 0*23 + 0*22 + 1*21 + 1*20 = 16+0+0+2+1 = 19.
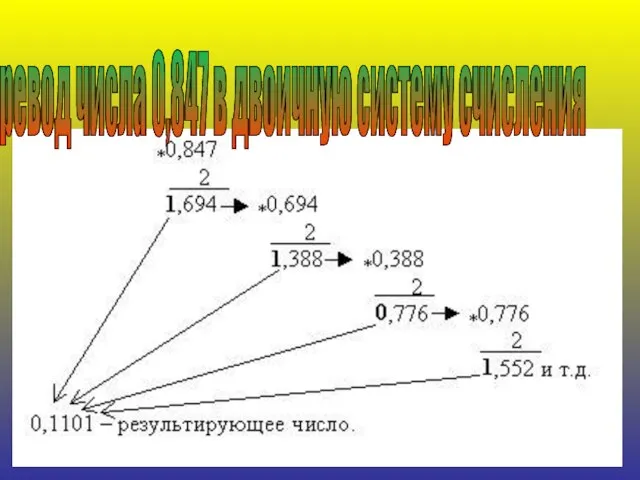
100112 = 19.

перевод числа 0,847 в двоичную систему счисления

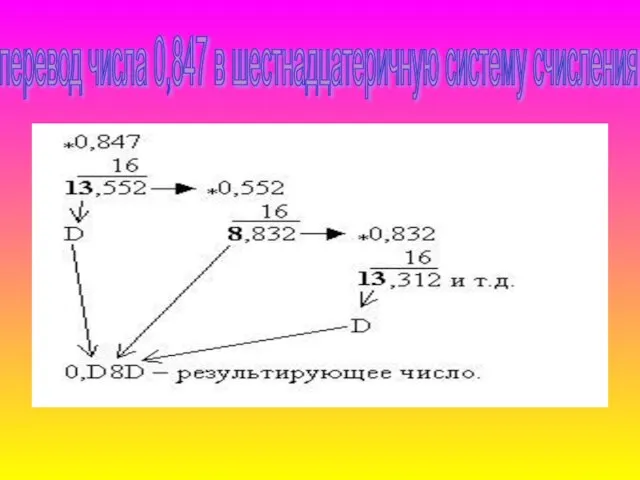
перевод числа 0,847 в шестнадцатеричную систему счисления

перевод из двоичной системы счисления в шестнадцатеричную числа 0,11012
11012 = D16. Тогда 0,11012 = 0,D16

перевод из двоичной системы счисления в шестнадцатеричную числа 0,00101012.
00102 = 102 = 216 и 10102 = A16.
Тогда 0,00101012 = 0,2A16.

перевод из шестнадцатеричной системы счисления в двоичную числа 0,2А16.
216 = 00102 и А16 = 10102.
0,2А16 = 0,001010102.
Отбросим в результате незначащий ноль и получим окончательный ответ:
0,2А16 = 0,00101012