Содержание
- 2. Решите уравнение: 4(х - 3) - 16 = 5(х - 5) 4х - 12 - 16
- 3. Решите устно рациональным способом: 0,3 (-0,6) - (-0,7) (-0,6) 0 17 -0,6
- 4. Что общего в этих уравнениях? Чем отличаются эти уравнения?
- 5. Разделите уравнения на группы. По какому принципу можно разделить уравнения?
- 6. Повторим определение модуля. Продолжите фразу: Модулем положительного числа… Модулем отрицательного числа… Модулем нуля…
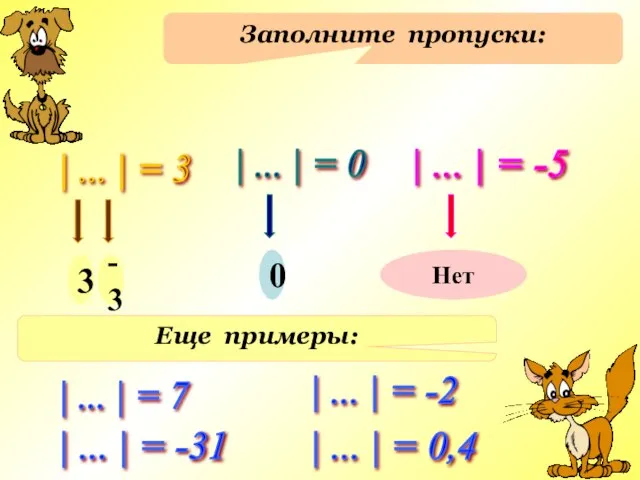
- 7. Заполните пропуски: | ... | = 3 | ... | = 0 | ... | =
- 8. Уравнения с переменной под знаком модуля решаются так: I | t | = a; a >
- 9. Решите уравнения: | 2 + x | = 4 | 4 + x | = 12
- 10. Уравнения с переменной под знаком модуля решаются так: II | t | = 0 t =
- 11. Решите уравнения: | 1 - 2x | = 0 | 7 + 2x | = 0
- 12. Уравнения с переменной под знаком модуля решаются так: III | t | = a; Нет корней
- 13. Решите уравнения: | 2x - 5 | = -7 | 0,5 + х| = -5 |
- 14. Повторение. Решение задач.
- 15. Три этапа решения задач. I Составление математической модели. II Работа c математической моделью. III Ответ на
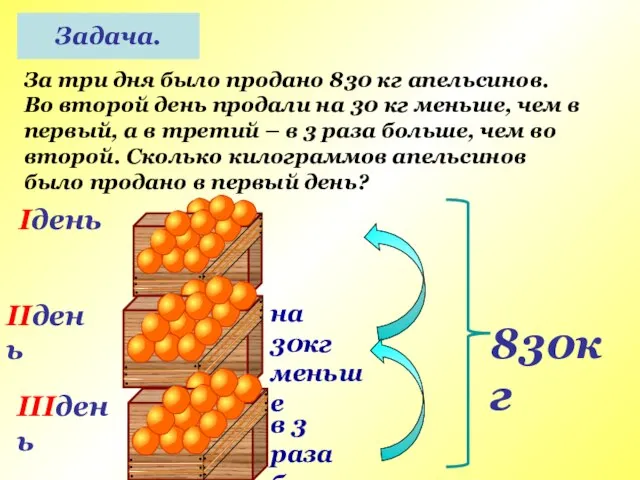
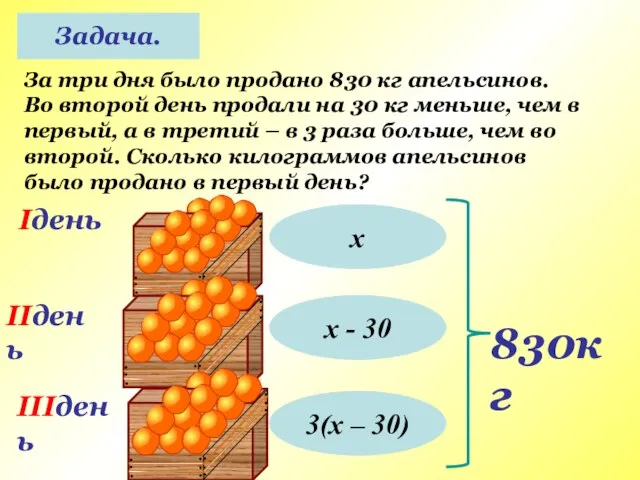
- 16. Задача. За три дня было продано 830 кг апельсинов. Во второй день продали на 30 кг
- 17. Задача. За три дня было продано 830 кг апельсинов. Во второй день продали на 30 кг
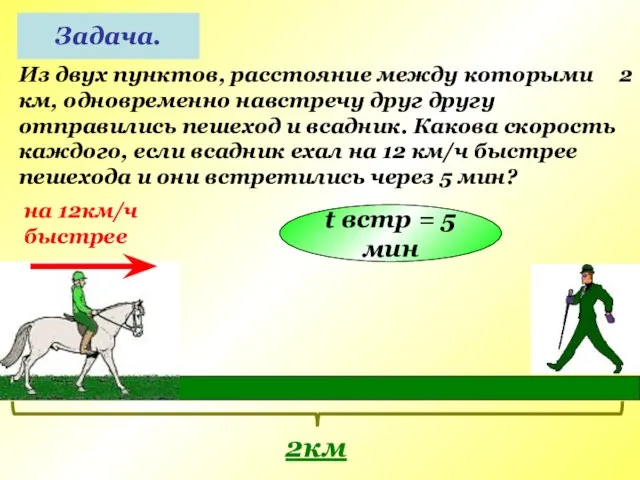
- 18. Задача. Из двух пунктов, расстояние между которыми 2 км, одновременно навстречу друг другу отправились пешеход и
- 19. на 12км/ч быстрее x км/ч (x+12)км/ч 2км t встр = 5 мин
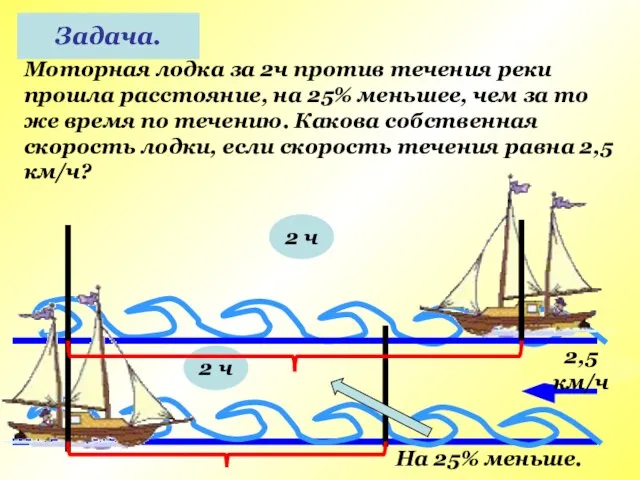
- 20. Моторная лодка за 2ч против течения реки прошла расстояние, на 25% меньшее, чем за то же
- 22. Скачать презентацию






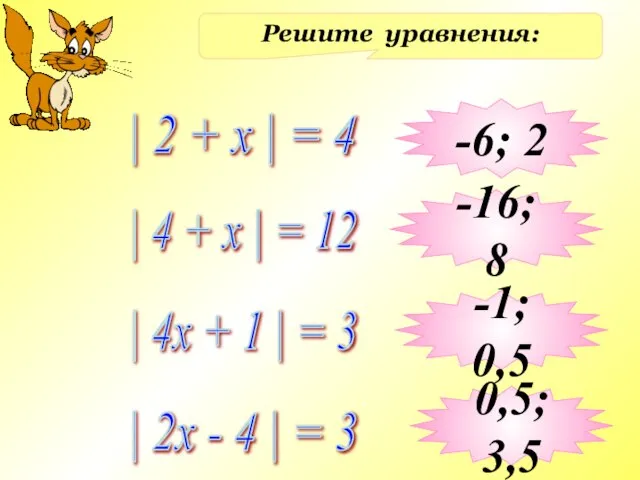







 Презентация на тему Восточная Сибирь
Презентация на тему Восточная Сибирь  Упрощение выражений
Упрощение выражений Проект «Аналогия» был запущен нами более десяти лет назад и возник как плод сочетания потенциалов юриста и бухгалтера с целью реше
Проект «Аналогия» был запущен нами более десяти лет назад и возник как плод сочетания потенциалов юриста и бухгалтера с целью реше Генеалогия
Генеалогия Колизей в Риме
Колизей в Риме 1С-Битрикс: Корпоративный портал
1С-Битрикс: Корпоративный портал Слова антонимы (Противоположности)
Слова антонимы (Противоположности) Cisco Solution Technology Integrator Сетевая безопасность для вертикальных рынков Решения для коммуникационных провайдеров СТАНДАРТ СЕТЕВОЙ БЕЗО
Cisco Solution Technology Integrator Сетевая безопасность для вертикальных рынков Решения для коммуникационных провайдеров СТАНДАРТ СЕТЕВОЙ БЕЗО Китайский новый год
Китайский новый год 20 причин любить Рёму
20 причин любить Рёму Путь. Перемещение. Определение координаты движущегося тела
Путь. Перемещение. Определение координаты движущегося тела Pancakes day
Pancakes day Критерии и методика отнесения документов к категории для служебного пользования
Критерии и методика отнесения документов к категории для служебного пользования Учебные видеоролики, как ресурс саморазвития
Учебные видеоролики, как ресурс саморазвития Система Box-Design & Nevo
Система Box-Design & Nevo Рекомендуемые подходы определения страховых резервов по договорам страхования жизни На основе Проекта Минфина Правил формирова
Рекомендуемые подходы определения страховых резервов по договорам страхования жизни На основе Проекта Минфина Правил формирова Дома гороскопа
Дома гороскопа Сложение и вычитание десятичных дробей.
Сложение и вычитание десятичных дробей. Судьба старославянизмов в русском языке
Судьба старославянизмов в русском языке Подготовка к написанию изложения по рассказу Л.Н.Толстого «Акула»
Подготовка к написанию изложения по рассказу Л.Н.Толстого «Акула» Обобщающий урок по теме:
Обобщающий урок по теме: Маркетинговые исследования
Маркетинговые исследования  Факторы развития когнитивных способностей в процессе обучения
Факторы развития когнитивных способностей в процессе обучения Доступ к данным на основе ado
Доступ к данным на основе ado Весна. Детские рисунки
Весна. Детские рисунки Декларация на товары
Декларация на товары Химическое действие света. Фотография
Химическое действие света. Фотография Моделирование, как метод познания (10 класс)
Моделирование, как метод познания (10 класс)