Содержание
- 2. Найдите площадь поверхности (внешней и внутренней) шляпы, размеры которой (в см) указаны на рисунке. 1) Если
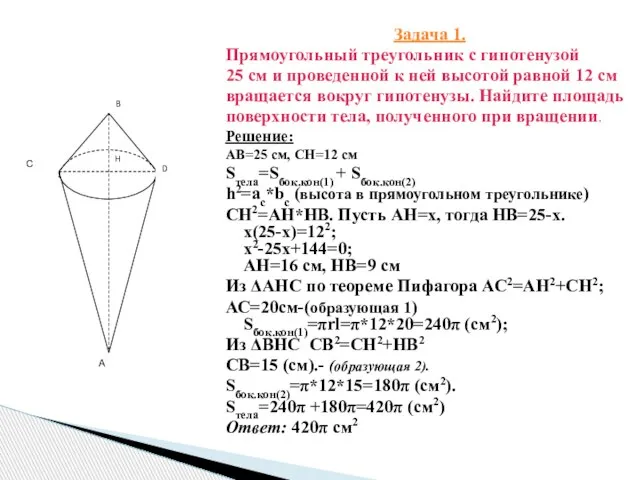
- 3. Задача 1. Прямоугольный треугольник с гипотенузой 25 см и проведенной к ней высотой равной 12 см
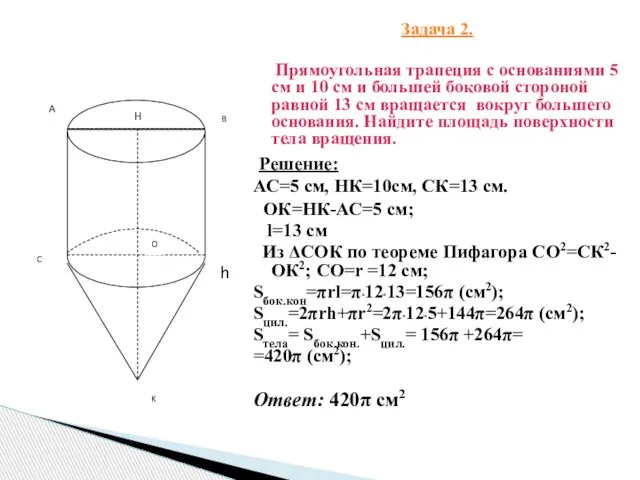
- 4. Задача 2. Прямоугольная трапеция с основаниями 5 см и 10 см и большей боковой стороной равной
- 5. Задача 3. Прямоугольная трапеция с основаниями 5 см и 10 см и большей боковой стороной равной
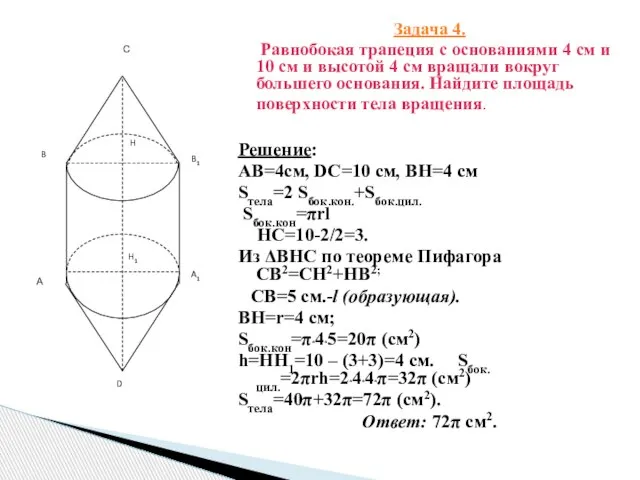
- 6. Задача 4. Равнобокая трапеция с основаниями 4 см и 10 см и высотой 4 см вращали
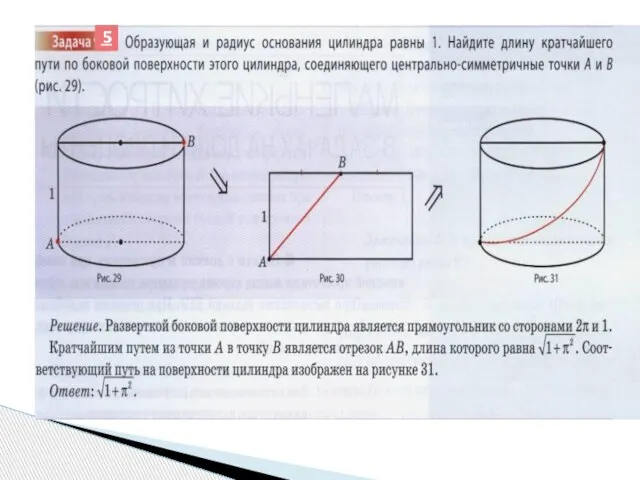
- 7. 5
- 8. 6
- 9. 7
- 10. Дано два цилиндра. Объем первого равен 12 м3. Радиус основания второго в два раза меньше, чем
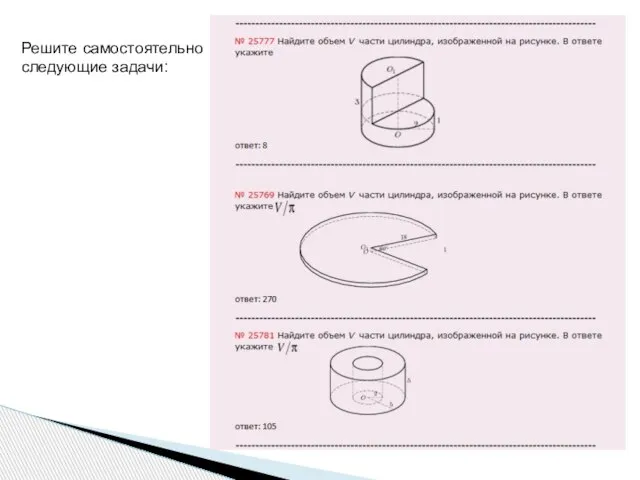
- 11. Решите самостоятельно следующие задачи:
- 13. Скачать презентацию





 Отчет
Отчет ГЕОГРАФИЯ
ГЕОГРАФИЯ Школа музыки GUITARDO
Школа музыки GUITARDO Презентация на тему Русская икона. Древнерусская живопись
Презентация на тему Русская икона. Древнерусская живопись Прочитай загадку, найди отгадку
Прочитай загадку, найди отгадку Два художника (Дружба Чехова и Левитана)
Два художника (Дружба Чехова и Левитана) Спирты
Спирты Презентация на тему Час общения «Времена года»
Презентация на тему Час общения «Времена года» Презентация на тему Платоники и Элидо-эритрийская школа
Презентация на тему Платоники и Элидо-эритрийская школа Стратегия муниципальных выборов в новой реальности
Стратегия муниципальных выборов в новой реальности Презентация на тему Этические правила служебного поведения и проф. служебной деятельности гос. гражданских служащих РФ
Презентация на тему Этические правила служебного поведения и проф. служебной деятельности гос. гражданских служащих РФ  НАИМЕНОВАНИЕ ОРГАНИЗАЦИИ КАК ПРЕДМЕТ Васильева Анна Сергеевна зав. сектором электронного каталога отдела научной обработки ф
НАИМЕНОВАНИЕ ОРГАНИЗАЦИИ КАК ПРЕДМЕТ Васильева Анна Сергеевна зав. сектором электронного каталога отдела научной обработки ф Презентация на тему Правила поведения на железной дороге (3 класс)
Презентация на тему Правила поведения на железной дороге (3 класс) ПОЛОЖЕНИЕ о выборах членовМолодежного парламентаМО «Увинский район»
ПОЛОЖЕНИЕ о выборах членовМолодежного парламентаМО «Увинский район» Мастер-класс Изготовление театральной куклы
Мастер-класс Изготовление театральной куклы The Family Law
The Family Law  Бойко Алесандра
Бойко Алесандра Elektron sənəd. Dövri̇yyəsi̇ si̇stemi̇
Elektron sənəd. Dövri̇yyəsi̇ si̇stemi̇ Правовые дебаты: «ЗА» и «ПРОТИВ»
Правовые дебаты: «ЗА» и «ПРОТИВ» Благотворительная программа «Подарим детям сказку»
Благотворительная программа «Подарим детям сказку» ЛУГАНСКАЯ ОБЛАСТЬ, УКРАИНА
ЛУГАНСКАЯ ОБЛАСТЬ, УКРАИНА Направления современной живописи
Направления современной живописи Натрий
Натрий Электронная физкультминутка boom-boom
Электронная физкультминутка boom-boom Царь Иван Грозный
Царь Иван Грозный Размещение рекламы в ВУЗах РФ
Размещение рекламы в ВУЗах РФ Психология общения Берн
Психология общения Берн «Моя математика» 1 класс
«Моя математика» 1 класс