Содержание
- 2. 1%−это сотая часть рассматриваемой величины (52% от х кг − это 0,52х кг); Если в смеси
- 3. вода кислота вода вода кислота кислота 600 г 15% 10% 30% Х г 600−Х г 0,3Х
- 4. медь олово медь олово олово 15+Х кг 70% 60% 15 кг Х кг 0,6∙15 кг 0,7(15+Х)
- 5. алюминий магний алюминий магний магний 22+Х+15=37+Х кг Х+15 кг Х кг 22+Х кг 100∙(Х+15)/(37+Х) % +
- 6. Смесь, состоящая из двух веществ, весит 18 кг. После того, как из нее выделили 40 %
- 7. медь цинк медь медь цинк 2Х+40 кг 2Х−60 кг 100 кг х−60 кг 0,7(2Х+40) кг +
- 8. Для приготовления лекарства потребовался 76 %-ный спирт. Провизор налил в колбу 220 г 95 %-ного спирта.
- 10. Скачать презентацию
Слайд 21%−это сотая часть рассматриваемой величины (52% от х кг − это 0,52х
1%−это сотая часть рассматриваемой величины (52% от х кг − это 0,52х

Если в смеси растворов объемом V (массой m) нас интересует компонент объемом V0 (массой m0), то процентное содержание этого вещества можно просчитать по формуле:
P0=(V0/V)∙100% или P0=(m0/m) ∙100% ;
В качестве неизвестных обычно выбирают объемы или массы компонентов смеси (сплава);
Складывать, уравнивать, сравнивать можно только массовые доли одного и того же вещества, или веществ в смеси (сплаве).
При решении таких задач важно знать, что:
Слайд 3вода
кислота
вода
вода
кислота
кислота
600 г
15%
10%
30%
Х г
600−Х г
0,3Х г
0,1(600−Х) г
0,15∙600 г
+
=
0,3Х+0,1(600−Х)=0,15∙600, Х=150
150 г первого раствора, тогда
вода
кислота
вода
вода
кислота
кислота
600 г
15%
10%
30%
Х г
600−Х г
0,3Х г
0,1(600−Х) г
0,15∙600 г
+
=
0,3Х+0,1(600−Х)=0,15∙600, Х=150
150 г первого раствора, тогда
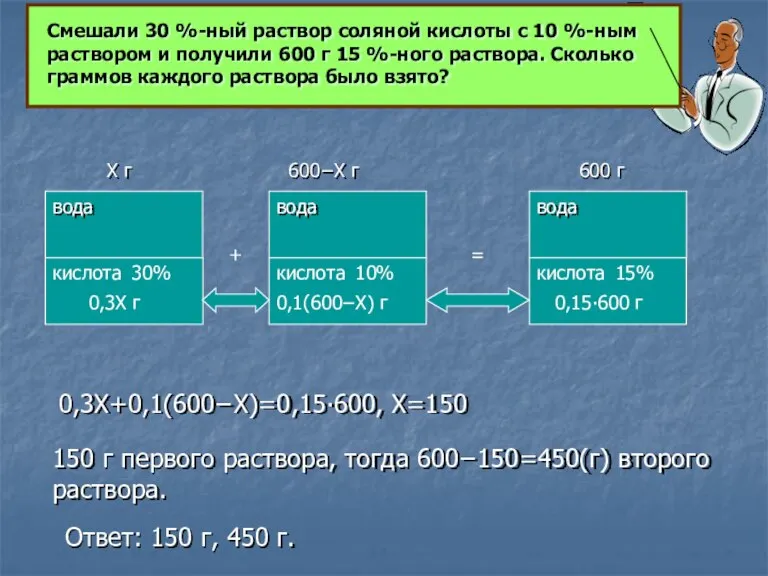
Ответ: 150 г, 450 г.
Смешали 30 %-ный раствор соляной кислоты с 10 %-ным раствором и получили 600 г 15 %-ного раствора. Сколько граммов каждого раствора было взято?
Слайд 4медь
олово
медь
олово
олово
15+Х кг
70%
60%
15 кг
Х кг
0,6∙15 кг
0,7(15+Х) кг
+
=
0,6∙15+Х=0,7(15+Х), Х=5.
5 кг олова надо добавить, чтобы
медь
олово
медь
олово
олово
15+Х кг
70%
60%
15 кг
Х кг
0,6∙15 кг
0,7(15+Х) кг
+
=
0,6∙15+Х=0,7(15+Х), Х=5.
5 кг олова надо добавить, чтобы

Ответ: 5 кг.
Имеется кусок сплава меди с оловом массой 15 кг, содержащий 40% меди. Сколько чистого олова надо прибавить к этому куску, чтобы получившийся новый сплав содержал 30 % меди?
40%
30%
Слайд 5алюминий
магний
алюминий
магний
магний
22+Х+15=37+Х кг
Х+15 кг
Х кг
22+Х кг
100∙(Х+15)/(37+Х) %
+
=
100Х/(22+Х)+33=100(Х+15)/(37+Х), Х=3.
Таким образом, сплав первоначально весил 25
алюминий
магний
алюминий
магний
магний
22+Х+15=37+Х кг
Х+15 кг
Х кг
22+Х кг
100∙(Х+15)/(37+Х) %
+
=
100Х/(22+Х)+33=100(Х+15)/(37+Х), Х=3.
Таким образом, сплав первоначально весил 25
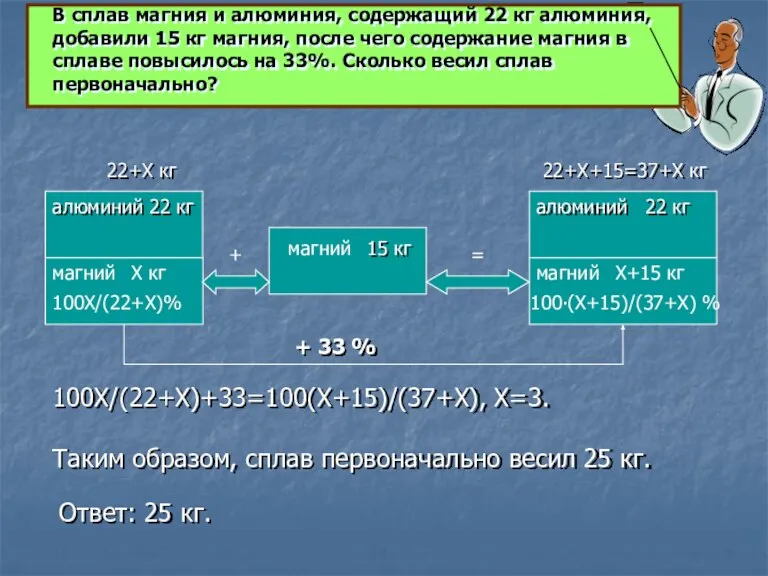
Ответ: 25 кг.
В сплав магния и алюминия, содержащий 22 кг алюминия, добавили 15 кг магния, после чего содержание магния в сплаве повысилось на 33%. Сколько весил сплав первоначально?
22 кг
15 кг
100Х/(22+Х)%
+ 33 %
22 кг
Слайд 6Смесь, состоящая из двух веществ, весит 18 кг. После того, как из
Смесь, состоящая из двух веществ, весит 18 кг. После того, как из

1 вещество
2 вещество
40 %
25 %
18 кг
60 %
75 %
Х кг
У кг
0,6Х кг
0,75У кг
+
=
=
Х+У=18,
0,6Х=0,75У.
Х=10,
У=8.
1-го вещества было 10 кг, а 2-го вещества было 8 кг.
Ответ: 10 кг, 8 кг.
Слайд 7медь
цинк
медь
медь
цинк
2Х+40 кг
2Х−60 кг
100 кг
х−60 кг
0,7(2Х+40) кг
+
=
Х+100=0,7(2Х+40), Х=180.
180 кг было меди в первоначальном
медь
цинк
медь
медь
цинк
2Х+40 кг
2Х−60 кг
100 кг
х−60 кг
0,7(2Х+40) кг
+
=
Х+100=0,7(2Х+40), Х=180.
180 кг было меди в первоначальном
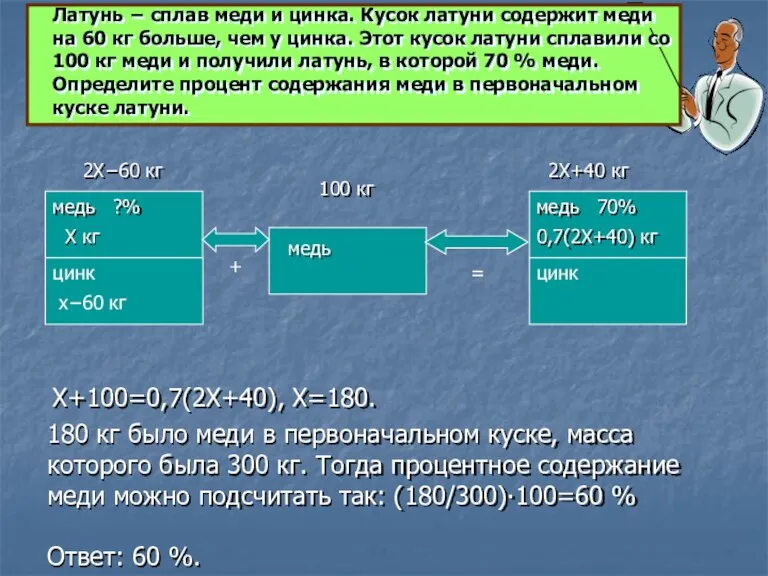
Ответ: 60 %.
Латунь − сплав меди и цинка. Кусок латуни содержит меди на 60 кг больше, чем у цинка. Этот кусок латуни сплавили со 100 кг меди и получили латунь, в которой 70 % меди. Определите процент содержания меди в первоначальном куске латуни.
?%
70%
Х кг
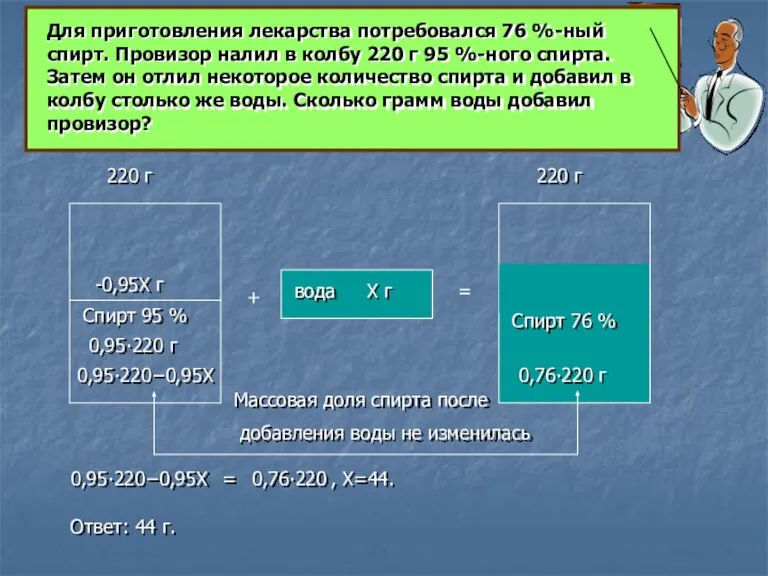
Слайд 8Для приготовления лекарства потребовался 76 %-ный спирт. Провизор налил в колбу 220
Для приготовления лекарства потребовался 76 %-ный спирт. Провизор налил в колбу 220
220 г
Спирт 95 %
+
=
220 г
Спирт 76 %
вода
0,95∙220 г
-0,95Х г
Х г
0,95∙220−0,95Х
0,76∙220 г
Массовая доля спирта после
добавления воды не изменилась
0,95∙220−0,95Х
=
0,76∙220
, Х=44.
Ответ: 44 г.
 Презентация на тему Наука и философия Естественно-научные и социально-гуманитарные знания
Презентация на тему Наука и философия Естественно-научные и социально-гуманитарные знания  Эволюция культуры человека
Эволюция культуры человека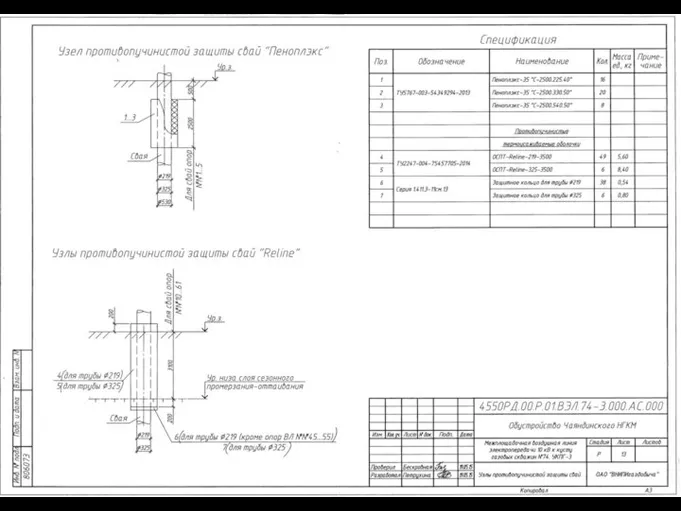 Проектное решение ОСПТ Reline линии электропередач
Проектное решение ОСПТ Reline линии электропередач С Международным женским днём 8 Марта!
С Международным женским днём 8 Марта! Конкурентная политика туристского агентства
Конкурентная политика туристского агентства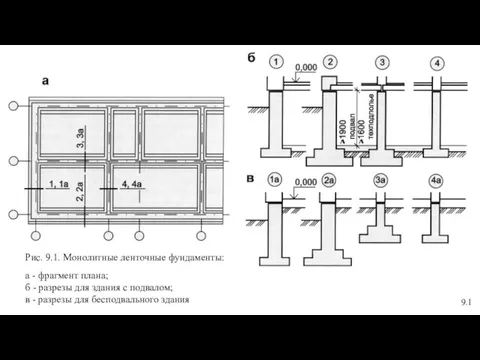 Монолитные ленточные фундаменты
Монолитные ленточные фундаменты Законодательное обеспечение охраны труда
Законодательное обеспечение охраны труда Презентация на тему Амазонка
Презентация на тему Амазонка требования к фгос пекарь 1-2урок
требования к фгос пекарь 1-2урок Александр Александрович Блок
Александр Александрович Блок Имя числительное.
Имя числительное. Великие праздники Христа
Великие праздники Христа О наркотиках и наркомании
О наркотиках и наркомании Проект.pptx презентация ШЭПР
Проект.pptx презентация ШЭПР Описание франшизыредакция от 6 ноября 2009 г.
Описание франшизыредакция от 6 ноября 2009 г. Нерабочие дни в октябре - ноябре 2021 года
Нерабочие дни в октябре - ноябре 2021 года Животный и растительный мир Калининградской области
Животный и растительный мир Калининградской области Гладь озерная на полотне
Гладь озерная на полотне мировой экон. кризис
мировой экон. кризис Развитие творческого потенциала и природных способностей детей младшего и среднего возраста в условиях клуба по месту жительства
Развитие творческого потенциала и природных способностей детей младшего и среднего возраста в условиях клуба по месту жительства Зимнее настроение. Выставка творческих работ по изобразительному искусству
Зимнее настроение. Выставка творческих работ по изобразительному искусству Современные технологии и условия их обмена
Современные технологии и условия их обмена Сүз ясалышы ысуллары
Сүз ясалышы ысуллары Презентация на тему СОСТОЯНИЕ ХЛОПЧАТОБУМАЖНОЙ ОТРАСЛИ РОССИИ
Презентация на тему СОСТОЯНИЕ ХЛОПЧАТОБУМАЖНОЙ ОТРАСЛИ РОССИИ  Мы быстро принимаем решения
Мы быстро принимаем решения Дизайн автобуса футбольного клуба
Дизайн автобуса футбольного клуба Развитие представлений о Солнечной системе
Развитие представлений о Солнечной системе Где жили динозавры (1 класс)
Где жили динозавры (1 класс)