Решение задач на составление уравнений. 6 класс

Тема урока
Решение задач
на составление уравнений

Мухаммед аль-Хорезми
В истории арифметики и алгебры большое значение имеют труды Мухаммеда аль-Хорезми (т.е. уроженец
Хорезма в Узбекистане,
783 – 850 гг.). Он написал книгу, посвященную решению уравнений, которая называлась «Китаб аль-джабр валь мукабала», т.е. «Книга о восстановлении и противопоставлении».

Исаак Ньютон
(4.01.1643–31.03.1727)
Исаак Ньютон — английский физик, математик, механик и астроном, родился в Линкольншире в семье землевладельца. С 1661 года Ньютон учился в Кембридже у Исаака Барроу, который в 1669 году передал профессорскую кафедру своему выдающемуся ученику, открыто признав его превосходство. Ньютон работал в Кембридже до 1696 года, когда он занял пост инспектора, а позже — директора Монетного двора. Похоронен Ньютон в Вестминстерском аббатстве.

Устно
Используя данные рисунки, составьте выражения,
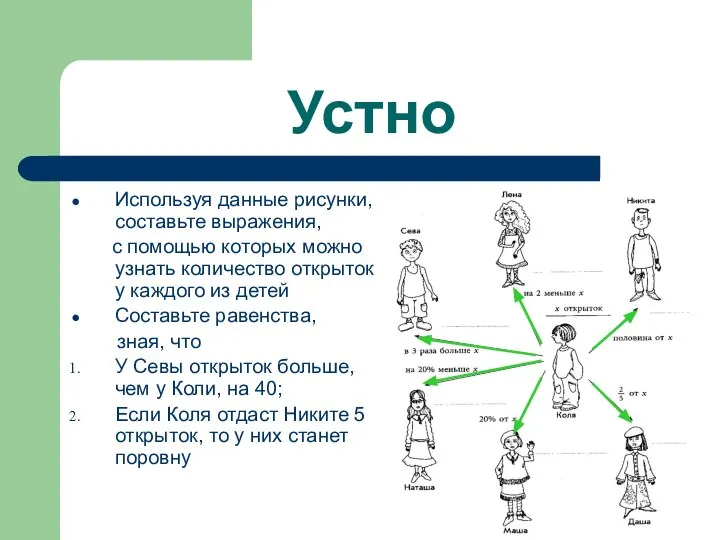
с помощью которых можно узнать количество открыток у каждого из детей
Составьте равенства,
зная, что
У Севы открыток больше, чем у Коли, на 40;
Если Коля отдаст Никите 5 открыток, то у них станет поровну

Ответь на вопросы
Какие три этапа математического моделирования используются при решении задачи?
Какие шаги необходимо выполнить, чтобы составить математическую модель задачи?
Какие формы записи предлагаются при составлении математической модели? Какая запись вам больше понравилась?
Какие шаги необходимо выполнить, чтобы решить полученное уравнение?
В чем состоит третий этап математического моделирования?

Этапы математического моделирования
составление математической модели
анализ задачи
схематическая запись задачи
запись уравнения
работа с математической моделью
ответ на вопрос задачи

Анализ задачи
Было
1 – ? в 3р. больше, чем
2 - ?
Стало поровну, после того как
1 – взяли 5 л
2 – добавили 5 л

Схематическая запись-1 задачи
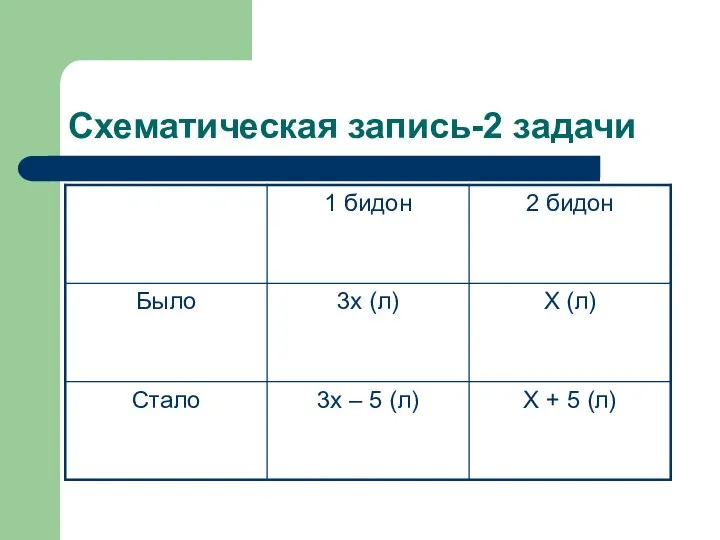
Пусть х л – количество молока, которое было до переливания во 2 бидоне. Тогда в первом бидоне его было 3х л.
После переливания в 1 бидоне осталось
(8х – 5) л молока, а во 2 стало (х + 5) л.
По условию задачи известно, что после переливания в обоих бидонах молока стало поровну. Составим уравнение
3х – 5 = х + 5

Схематическая запись-2 задачи

Выполни тест!
В одном шкафу было в 4 раза меньше книг, чем в другом. Когда в первый шкаф положили 17 книг, а со второго взяли 25, то в обоих шкафах книг стало поровну. Сколько книг было в каждом шкафу сначала?
Пусть х число книг в 1 шкафу. Какое из уравнений соответствует условию задачи?
А. х + 17 = х : 4 -25 Б. х + 17 = 4х – 25
В. х – 25 = х : 4 + 17 Г. 4х – 17 = х + 25

Решай дальше!
В двух коробках было поровну конфет. После того, как из первой коробки взяли 10 конфет, а из другой – 28 конфет, в первой коробке стало в 4 раза больше, чем во второй. Сколько конфет было в каждой коробке первоначально?
Пусть х число конфет в в каждой коробке первоначально. Какое из уравнений соответствует условию задачи?
А. 4(х – 10) = х - 28 Б. 4х – 10 = х - 28
В. Х – 10 = 4х – 28 В. Х – 10 = 4х – 28 Г. х – 10 = 4(х – 28)

Проверь себя!

Молодец!