Решение задач в MS Excel

Содержание:
Табулирование функции и построение графика.
2. Решение системы линейных уравнений.
А) Используя формулы массива.
Б) Используя метод Крамера.
3. Решение нелинейных уравнений.
А) Метод последовательных приближений.
Б) Метод подборов параметров Goal Seek.
************

Табулирование функции и построение графика.
***********
Протабулировать функцию y=cosx+sinx на отрезке [-2П, 2П], Н=П/18 и построить диаграмму.
Задание.
Строим таблицу значений для данной функции;

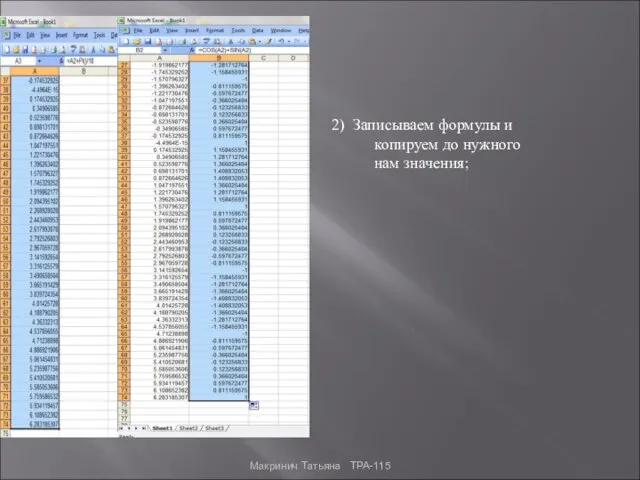
2) Записываем формулы и копируем до нужного нам значения;
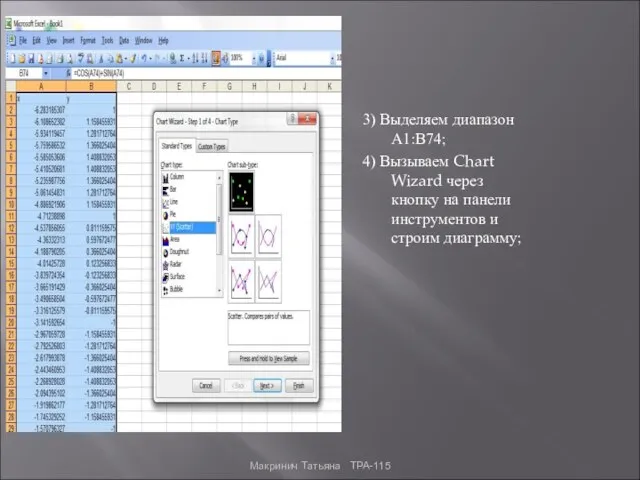
Макринич Татьяна ТРА-115

3) Выделяем диапазон А1:В74;
4) Вызываем Chart Wizard через кнопку на панели инструментов и строим диаграмму;
Макринич Татьяна ТРА-115

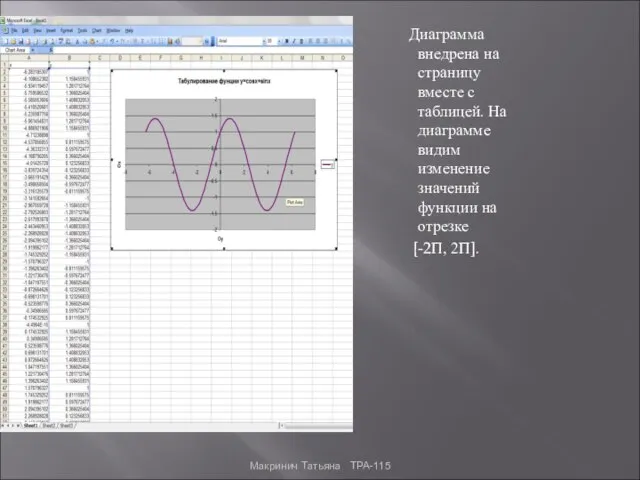
Диаграмма внедрена на страницу вместе с таблицей. На диаграмме видим изменение значений функции на отрезке
[-2П, 2П].
Макринич Татьяна ТРА-115

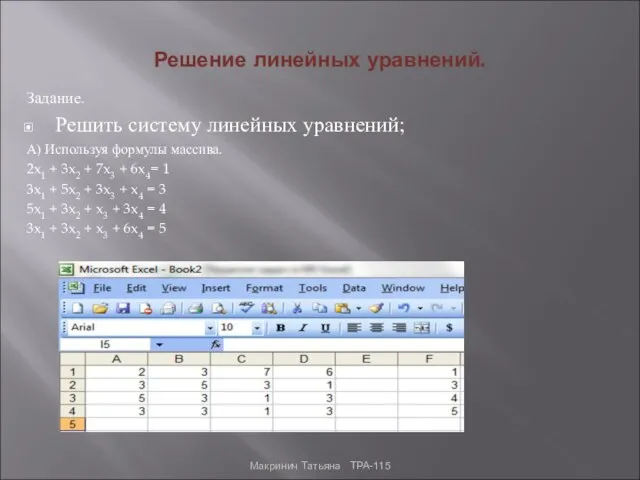
Решение линейных уравнений.
Задание.
Решить систему линейных уравнений;
А) Используя формулы массива.
2x1 + 3x2 + 7x3 + 6x4= 1
3x1 + 5x2 + 3x3 + x4 = 3
5x1 + 3x2 + x3 + 3x4 = 4
3x1 + 3x2 + x3 + 6x4 = 5
Макринич Татьяна ТРА-115

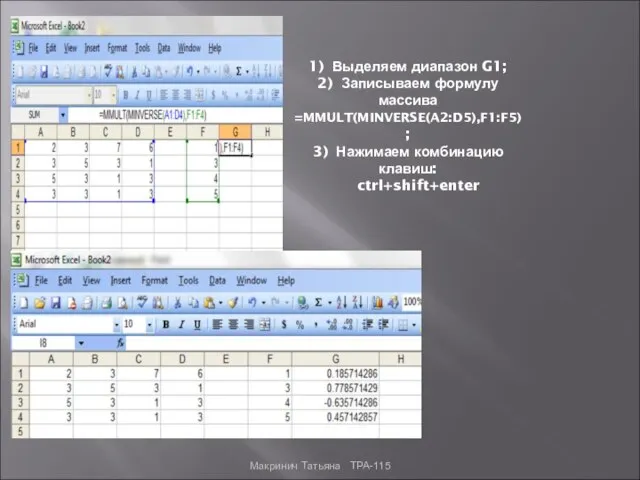
1) Выделяем диапазон G1;
2) Записываем формулу массива =MMULT(MINVERSE(A2:D5),F1:F5) ;
3) Нажимаем комбинацию клавиш: ctrl+shift+enter
Макринич Татьяна ТРА-115

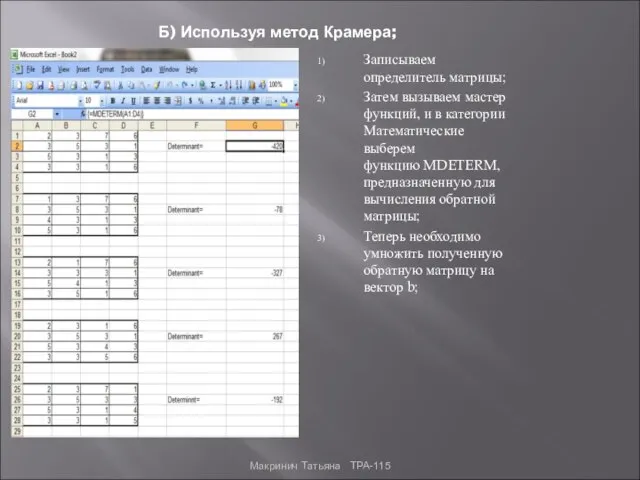
Б) Используя метод Крамера;
Записываем определитель матрицы;
Затем вызываем мастер функций, и в категории Математические выберем функцию MDETERM, предназначенную для вычисления обратной матрицы;
Теперь необходимо умножить полученную обратную матрицу на вектор b;
Макринич Татьяна ТРА-115

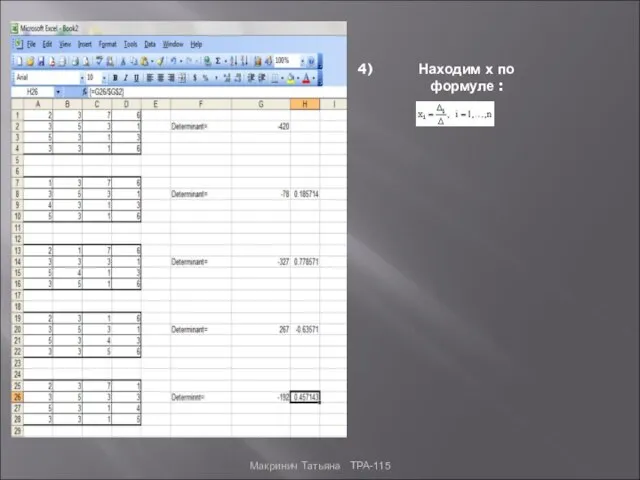
Находим х по формуле :
Макринич Татьяна ТРА-115

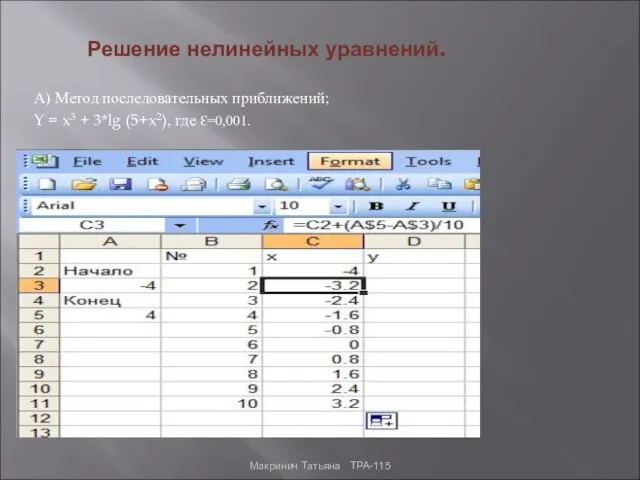
Решение нелинейных уравнений.
А) Метод последовательных приближений;
Y = x3 + 3*lg (5+x2), где Ɛ=0,001.
Макринич Татьяна ТРА-115

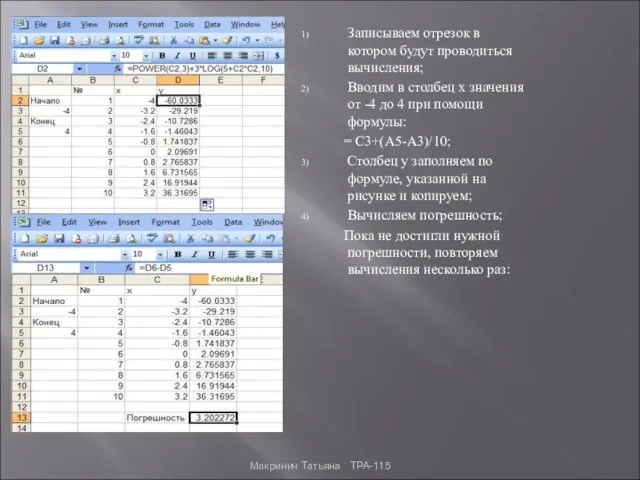
Записываем отрезок в котором будут проводиться вычисления;
Вводим в столбец х значения от -4 до 4 при помощи формулы:
= С3+(А5-А3)/10;
Столбец у заполняем по формуле, указанной на рисунке и копируем;
Вычисляем погрешность;
Пока не достигли нужной погрешности, повторяем вычисления несколько раз:
Макринич Татьяна ТРА-115

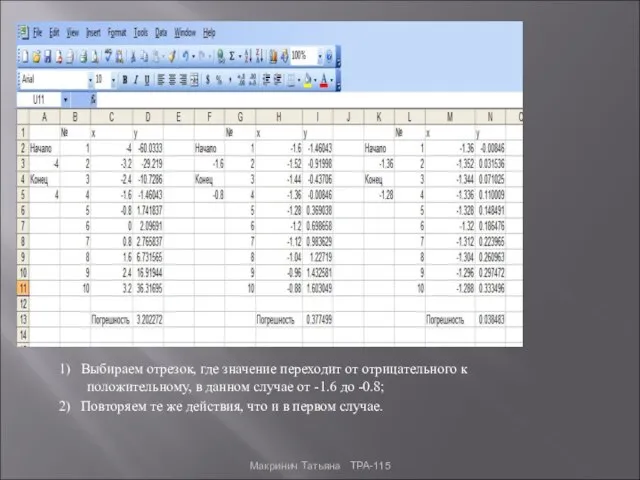
1) Выбираем отрезок, где значение переходит от отрицательного к положительному, в данном случае от -1.6 до -0.8;
2) Повторяем те же действия, что и в первом случае.
Макринич Татьяна ТРА-115

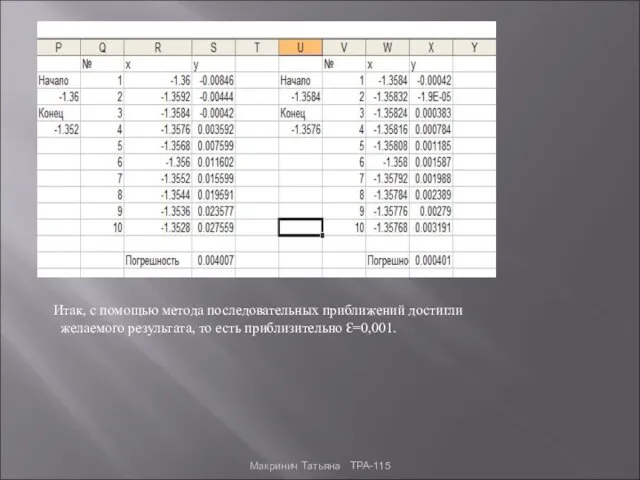
Итак, с помощью метода последовательных приближений достигли желаемого результата, то есть приблизительно Ɛ=0,001.
Макринич Татьяна ТРА-115