Решение задний В9

*
№1. Площадь поверхности куба равна 18. Найдите его диагональ
А
В
С
D
A1
B1
C1
D1
Пусть ребро куба равно а.

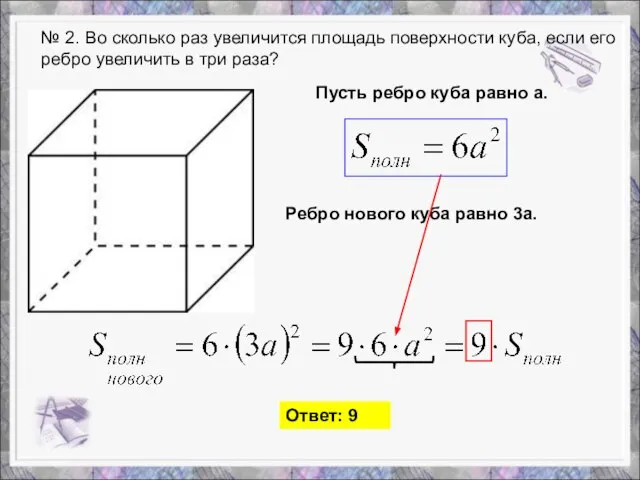
№ 2. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза?
Пусть ребро куба равно а.
Ребро нового куба равно 3а.
Ответ: 9

№ 3. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Пусть ребро куба равно а.
Ребро нового куба равно а+1.
Ответ: 4

№ 4. Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности.
Ответ: 22

№ 5. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.

№ 6. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.

№ 7. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Ответ: 288

№ 8. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
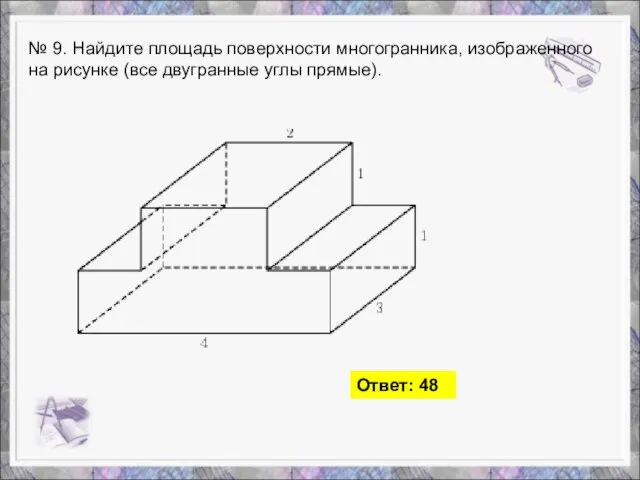
Ответ: 300

№ 9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 48

№ 10. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на
Ответ: 12

№ 11. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра.
Ответ: 8

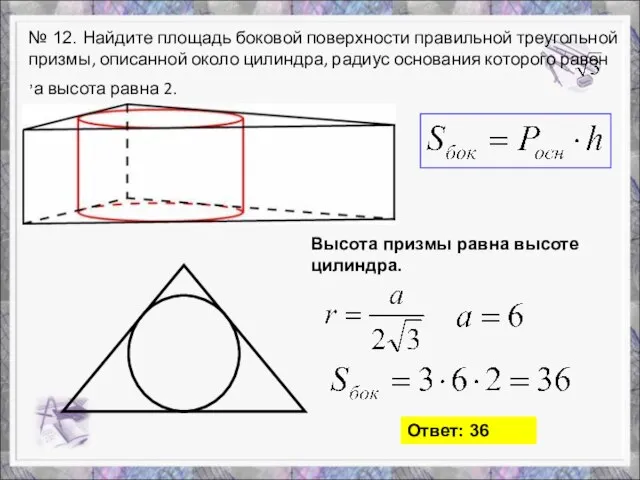
№ 12. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен ,
а высота равна 2.
Высота призмы равна высоте цилиндра.
Ответ: 36

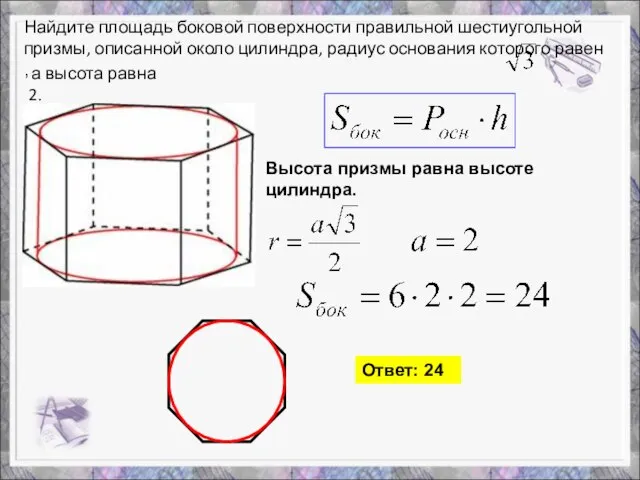
Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен ,
а высота равна 2.
Высота призмы равна высоте цилиндра.
Ответ: 24

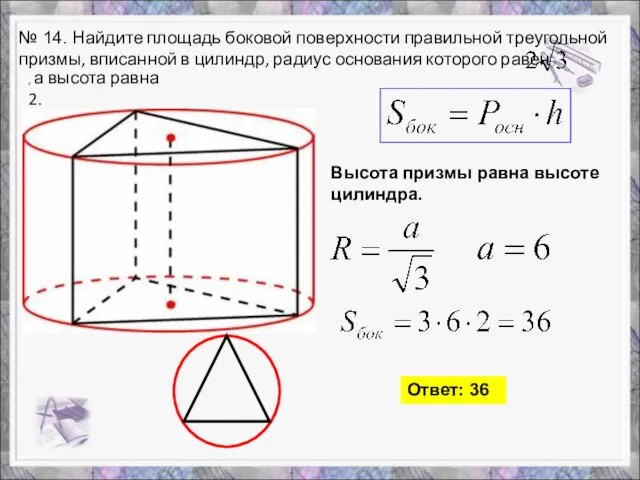
№ 14. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен
, а высота равна 2.
Высота призмы равна высоте цилиндра.
Ответ: 36