Определение графа

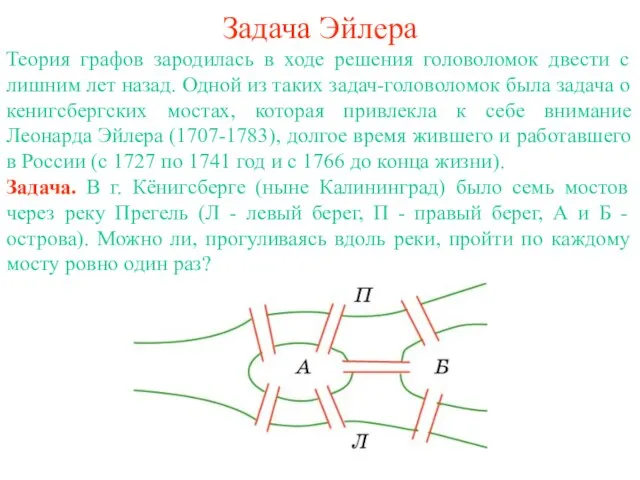
Задача Эйлера
Теория графов зародилась в ходе решения головоломок двести с лишним лет назад. Одной из таких задач-головоломок была задача о кенигсбергских мостах, которая привлекла к себе внимание Леонарда Эйлера (1707-1783), долгое время жившего и работавшего в России (с 1727 по 1741 год и с 1766 до конца жизни).
Задача. В г. Кёнигсберге (ныне Калининград) было семь мостов через реку Прегель (Л - левый берег, П - правый берег, А и Б - острова). Можно ли, прогуливаясь вдоль реки, пройти по каждому мосту ровно один раз?

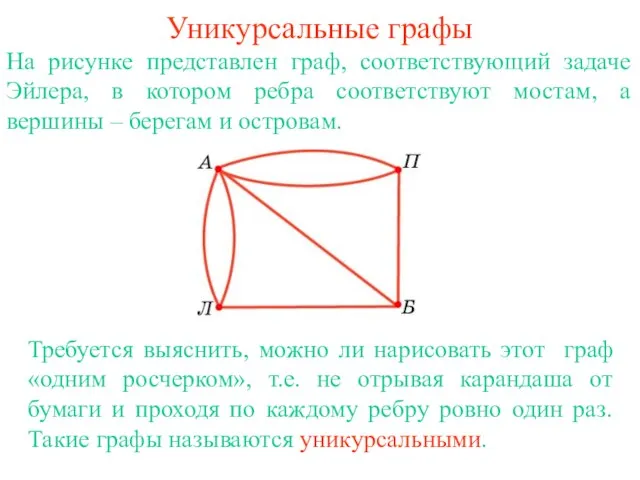
Уникурсальные графы
На рисунке представлен граф, соответствующий задаче Эйлера, в котором ребра соответствуют мостам, а вершины – берегам и островам.
Требуется выяснить, можно ли нарисовать этот граф «одним росчерком», т.е. не отрывая карандаша от бумаги и проходя по каждому ребру ровно один раз. Такие графы называются уникурсальными.

Теорема
Индексом вершины графа называется число ребер, сходящихся в этой вершине (ребра, с началом и концом в данной вершине считаются дважды).
Теорема. Для уникурсального графа число вершин нечетного индекса равно нулю или двум.
Доказательство. Если граф уникурсален, то у него есть начало и конец обхода. Остальные вершины имеют четный индекс, так как с каждым входом в такую вершину есть и выход. Если начало и конец не совпадают, то они являются единственными вершинами нечетного индекса. У начала выходов на один больше, чем входов, а у конца входов на один больше, чем выходов. Если начало совпадает с концом, то вершин с нечетным индексом нет.
Верно и обратное: Если у связного графа число вершин нечетного индекса равно нулю или двум, то он является уникурсальным.

Решение задачи Эйлера
Решение задачи Эйлера. Найдем индексы вершин графа задачи Эйлера. Вершина А имеет индекс 5, Б - 3, П - 3 и Л - 3. Таким образом, мы имеем четыре вершины нечетного индекса, и, следовательно, данный граф не является уникурсальным. Значит, нельзя пройти по каждому из семи мостов только один раз.

Вопрос 1
Какая фигура называется графом?
Ответ: Графом называется фигура, образованная конечным набором точек плоскости и отрезков, соединяющих некоторые из этих точек.

Вопрос 2
Какой граф называется уникурсальным?
Ответ: Граф называется уникурсальным, если его можно ли нарисовать «одним росчерком», т.е. не отрывая карандаша от бумаги и проходя по каждому ребру ровно один раз.

Вопрос 3
Что называется индексом вершины графа?
Ответ: Индексом вершины графа называется число ребер, сходящихся в этой вершине (ребра, с началом и концом в данной вершине считаются дважды).

Вопрос 4
Что можно сказать об индексах вершин уникурсального графа?
Ответ: Для уникурсального графа число вершин нечетного индекса равно нулю или двум.

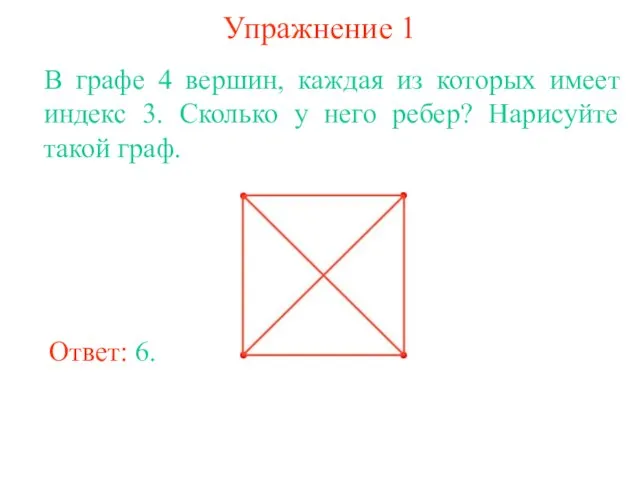
Упражнение 1
В графе 4 вершин, каждая из которых имеет индекс 3. Сколько у него ребер? Нарисуйте такой граф.

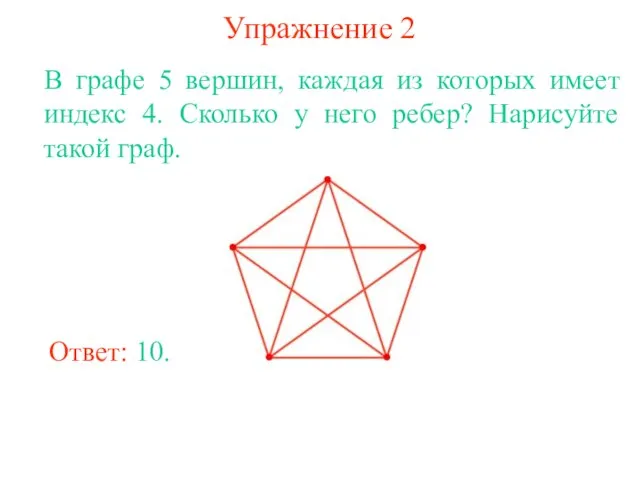
Упражнение 2
В графе 5 вершин, каждая из которых имеет индекс 4. Сколько у него ребер? Нарисуйте такой граф.

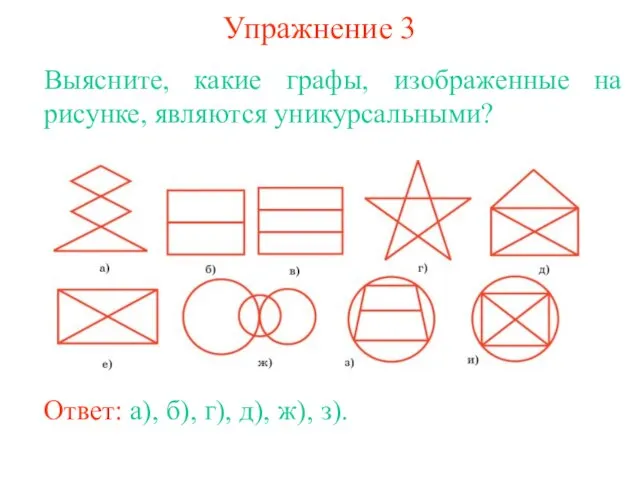
Упражнение 3
Выясните, какие графы, изображенные на рисунке, являются уникурсальными?
Ответ: а), б), г), д), ж), з).

Упражнение 4
Может ли граф иметь: а) одну вершину нечетного индекса; б) две вершины нечетного индекса; в) три вершины нечетного индекса; г) четыре вершины нечетного индекса?
Ответ: а), в) Нет; б), г) да.

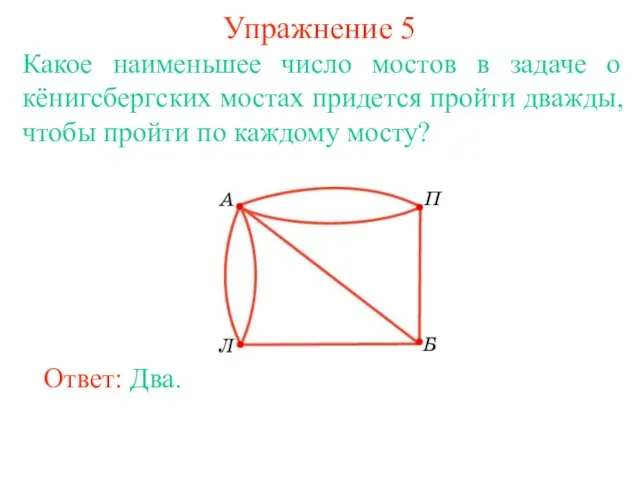
Упражнение 5
Какое наименьшее число мостов в задаче о кёнигсбергских мостах придется пройти дважды, чтобы пройти по каждому мосту?
Ответ: Два.

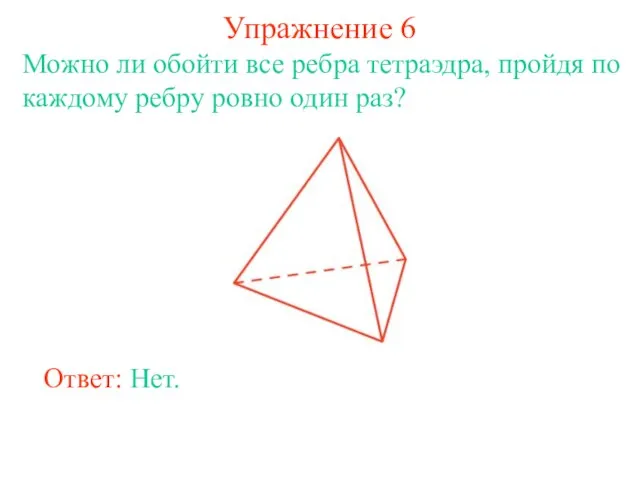
Упражнение 6
Можно ли обойти все ребра тетраэдра, пройдя по каждому ребру ровно один раз?
Ответ: Нет.

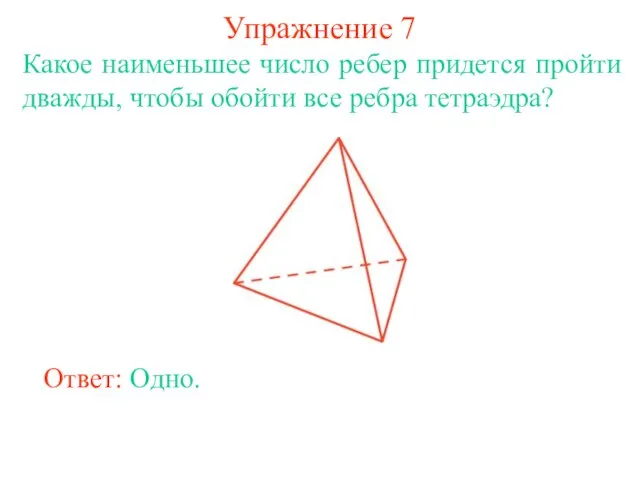
Упражнение 7
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра тетраэдра?
Ответ: Одно.

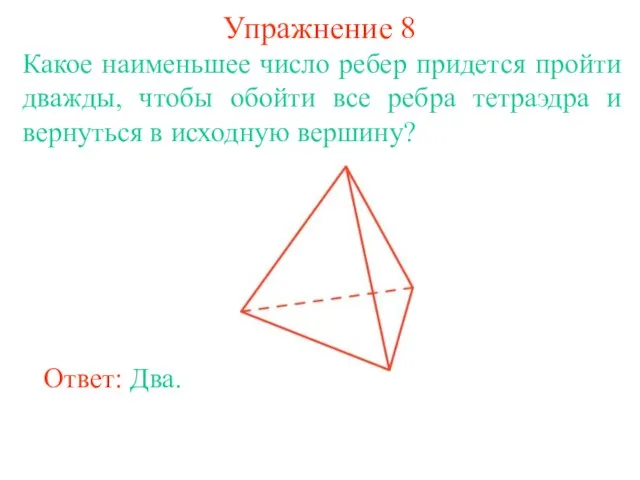
Упражнение 8
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра тетраэдра и вернуться в исходную вершину?
Ответ: Два.

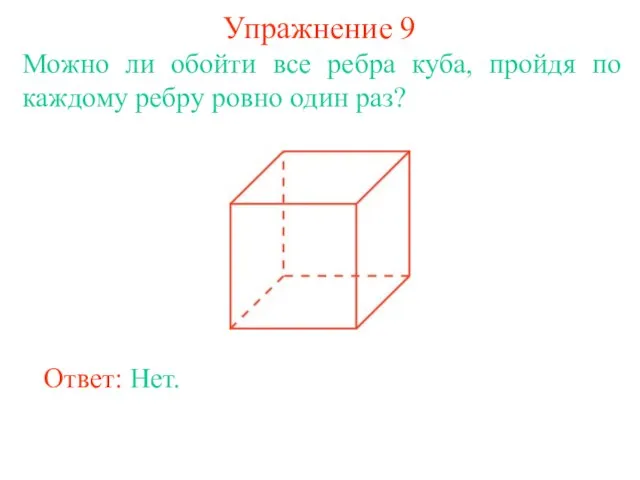
Упражнение 9
Можно ли обойти все ребра куба, пройдя по каждому ребру ровно один раз?
Ответ: Нет.

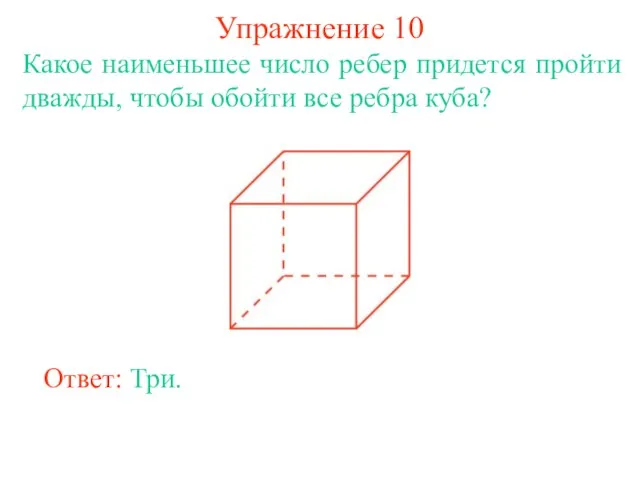
Упражнение 10
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра куба?
Ответ: Три.

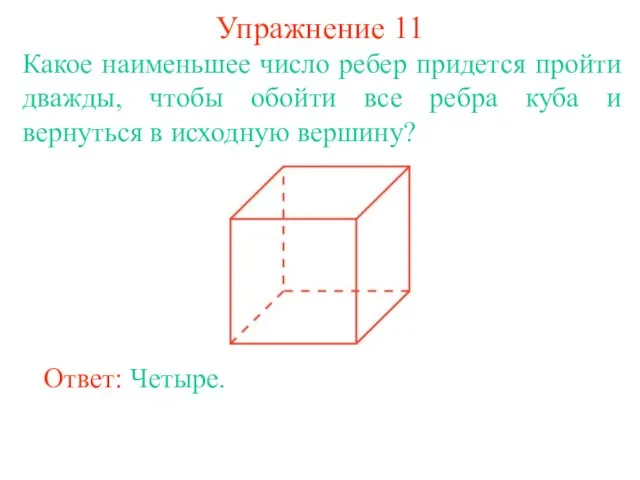
Упражнение 11
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра куба и вернуться в исходную вершину?
Ответ: Четыре.

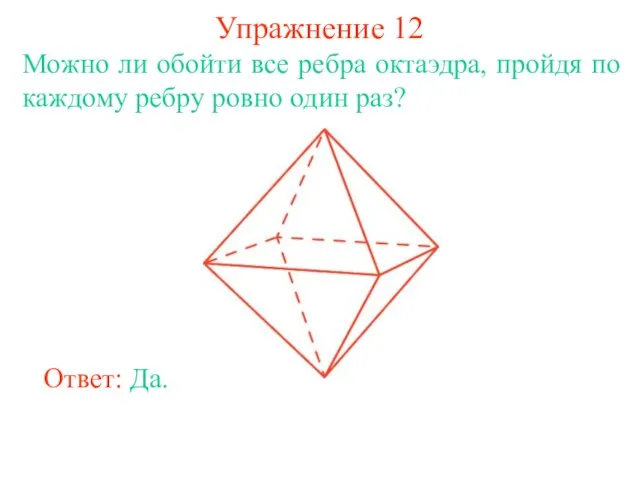
Упражнение 12
Можно ли обойти все ребра октаэдра, пройдя по каждому ребру ровно один раз?
Ответ: Да.

Упражнение 13
Можно ли обойти все ребра икосаэдра, пройдя по каждому ребру ровно один раз?
Ответ: Нет.

Упражнение 14
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра икосаэдра?
Ответ: Пять.

Упражнение 15
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра икосаэдра и вернуться в исходную вершину?
Ответ: Шесть.

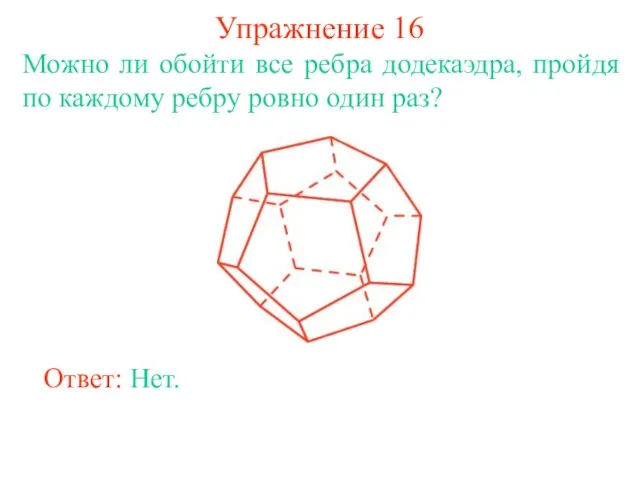
Упражнение 16
Можно ли обойти все ребра додекаэдра, пройдя по каждому ребру ровно один раз?
Ответ: Нет.

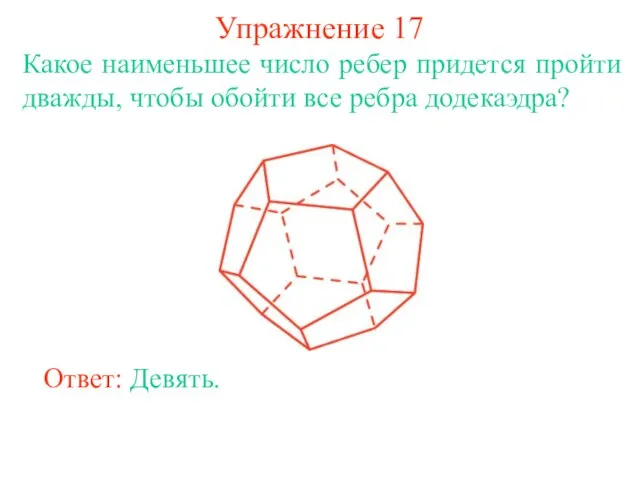
Упражнение 17
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра додекаэдра?
Ответ: Девять.

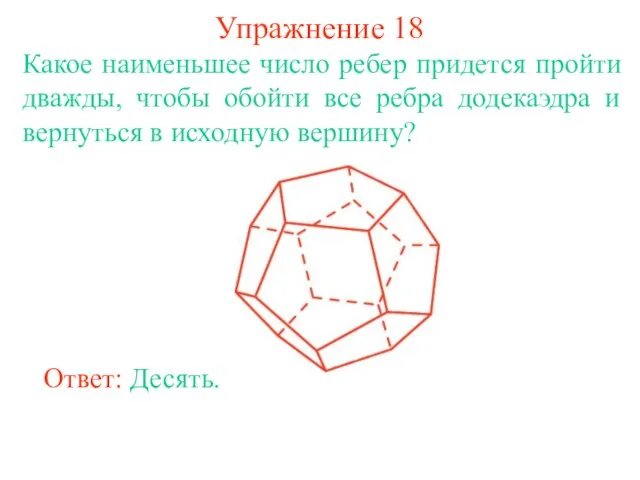
Упражнение 18
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра додекаэдра и вернуться в исходную вершину?
Ответ: Десять.