Решето Эратосфена

Тема:
«Решето
Эратосфена»

Идея возникновения проекта:
Ещё на уроке я поняла что такое простые и составные числа, но меня заинтересовали вопросы «а такие ли они простые «простые числа»?», сколько их вообще существует и можно ли обнаружить способ их нахождения
Мне была интересна и сама задача, и технология ИКТ, и сам продукт, т.е в виде чего будет представлена моя работа

Цель:
Нахождение простых чисел через
освоение метода «Решето Эратосфена», с последующим созданием медиапрезентации и её использования на уроках математики

Задачи:
Собрать и изучить материал
Применить понятия «кратные и делители числа» из предыдущего проекта
Рассмотреть отдельные варианты таблиц: до 48, до 100, до 150, до 200
Открыть какие-либо закономерности и свойства в ряду чисел
Обобщить полученные данные и сформулировать вывод

Актуальность:
Когда на форзаце учебника мы обнаружили таблицу простых чисел, то решили для себя, что авторы учебника придают этим числам большое значение и значит тема «простые числа» актуальна. И действительно, простые числа являются как бы «кирпичиками» из которых «строятся» остальные натуральные числа
И так как в настоящее время материал более наглядно представить можно с помощью компьютера, то решили применить ИКТ

Методы:
Поисковый
Метод (от частного к общему)
Технология:
Исследование

Новизна исследования:
Использование проектной технологии
Применение компьютера для нахождения простых чисел, применение эффекта анимации для показа определённой группы чисел

Объект исследования:
Метод поимки «простых чисел»
Предмет исследования:
Простые, составные числа

Источники:
Босова Л.Л. Информатика 6кл-Москва: БИНОМ,2007
Виленкин Н.Я. Математика 6кл-Москва: Просвещение,2002
Клименченко Д.В. Задачи по математике для любознательных-Москва: Просвещение,1992
Сост. Э-68 Савин А.П. Энциклопедический словарь юного математика-М.: Педагогика, 1989
Фотографии выполнены автором- Шульгиной Дашей, (панорамы на стенах лицея)

Практическое использование:
На уроках математики при изучении тем: «разложение чисел на множители», «приведение дробей к общему знаменателю»
Созданная таблица, красочно оформленная, поможет и другим учащимся разобраться в нахождении простых чисел

Гипотеза:
Мы освоим метод «Решето Эратосфе
на», но, вероятнее всего, не сможем найти самое большое простое число

Загадочные простые числа
Со времен древних греков простые числа оказываются столь же привлекательными, сколь и неуловимыми. Математики постоянно испытывают разные способы их «поимки», но до сих пор единственным по-настоящему эффективным остаётся тот способ, который найден александрийским математиком и астрономом Эратосфеном. А
этому методу уже около 2
тыс. лет! Этим же вопросом
занимался и древнегреческий
математик Эвклид

Интерес древних математиков
к простым числам связан с тем,
что любое число, либо простое,
либо может быть представлено
в виде произведения простых
ЧИСЕЛ, Т.Е. ПРОСТЫЕ ЧИСЛА-
это такие «кирпичики»,
из которых
строятся остальные
натуральные числа.

Почему решето?
Так как греки делали записи на покрытых воском табличках или на натянутом папирусе, а числа не вычёркивали, а выкалывали иглой, то таблица в конце вычислений
напоминала решето. Поэтому
метод Эратосфена и называл
ся «Решетом Эратосфена»: в
этом решете «отсеиваются»
простые числа от составных.

Определения
Если одно целое число можно разделить на другое без остатка, то второе число называется делителем первого.
Кратным натуральному числу а называют натуральное число, которое делится без остатка на а.
Натуральное число называется простым, если оно имеет только два делителя: единицу и само это число. Натуральное число является составным, если оно имеет более двух делителей.

Произвольный способ нахождения простых чисел
1 2 3 4 5 6 7 8 9 10 4пр.ч.
11 12 13 14 15 16 17 18 19 20 4пр.ч.
21 22 23 24 25 26 27 28 29 30 2пр.ч.
31 32 33 34 35 36 37 38 39 40 2пр.ч.
41 42 43 44 45 46 47 48 49 50 3пр.ч.
51 52 53 54 55 56 57 58 59 60 2пр.ч.

В этом случае мы не можем найти закономерность обнаружения простых чисел, они встречаются неравномерно. Мы находим их «вручную»
Это очень интересное свойство простых чисел, они отказываются подчиниться какой либо закономерности (для примера: чётные числа встречаются через одно число в ряду натуральных чисел; числа кратные 3 встречаются через два числа и т.д.).
Поэтому мы и обратились к варианту, который называется «Решетом Эратосфена»

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
Решето Эратосфена
3 простых числа
2 простых чисел
2 простых чисел
2 простых чисел
1 простое число
1 простое число
2 простых чисел
2 простых чисел
Всего-15 пр.чисел

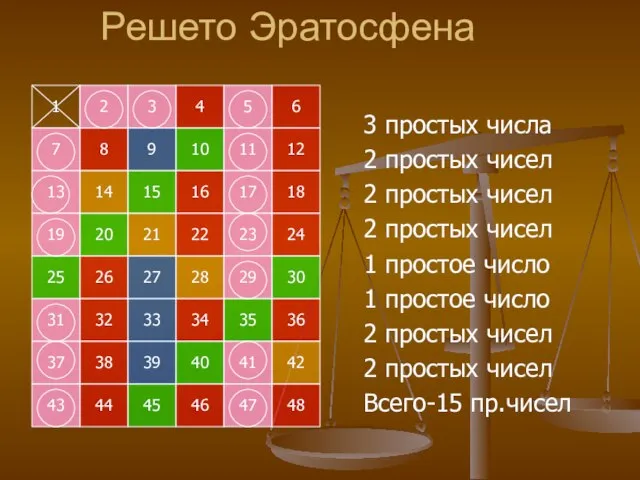
Алгоритм нахождения простых чисел
В этой таблице все простые числа, меньше 48 обведены кружками. Найдены они так. 1 имеет единственный делитель - себя, поэтому 1 не является простым числом, 2- наименьшее ( и единственное четное) простое число. Все остальные четные числа делятся на 2 и у них есть по крайней мере 3 делителя; поэтому могут быть вычеркнуты. Следующее не вычеркнутое число-3; оно имеет ровно 2 делителя, поэтому оно простое. Все остальные числа, кратные 3, вычеркиваются. Теперь первое не вычеркнутое число 5; оно простое, а все его кратные можно вычеркнуть. Продолжая вычеркивать кратные, можно отсеять все простые числа меньше 48.

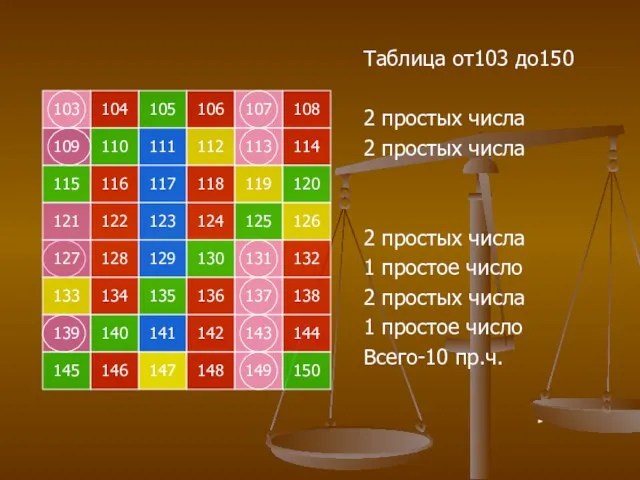
А теперь найдем все простые числа меньше 100, для этого продолжим таблицу до 102, дополнительно определяя делится ли число на 2,3,5,7

49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
Таблица от 49 до 102
1 простое число
1 простое число
1 простое число
2 простых числа
1 простое число
2 простых числа
1 простое число
2 простых числа
Всего-10 пр.чисел

103
105
104
107
106
108
109
111
110
113
112
114
115
117
116
119
118
120
121
123
122
125
124
126
127
129
128
131
130
132
133
135
134
137
136
138
139
141
140
143
142
144
145
147
146
149
148
150
Таблица от103 до150
2 простых числа
2 простых числа
2 простых числа
1 простое число
2 простых числа
1 простое число
Всего-10 пр.ч.

105
103
104
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
105
Таблица от103 до 198
-чётные числа
-числа кратные 5
(ПО ДИАГОНАЛЯМ СПРАВА НАЛЕВО)
-числа кратные 3
-числа кратные 7
(ПО ДИАГОНАЛЯМ СЛЕВА НАПРАВО)
-числа, которые
пока не поддаются
классификации
-простые числа

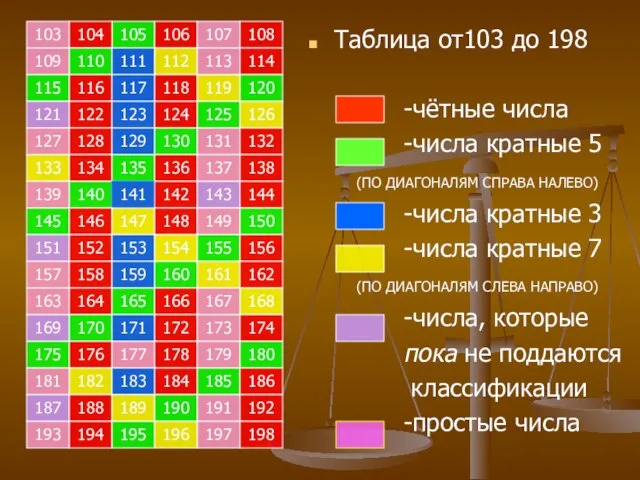
Итак, простыми числами от 1 до 200 являются 25 чисел на первой сотне натуральных чисел: 2,3,5,7,11,13,17,19,23,29,31,37,41,43,4753,59,61,67,71,73,79,83,89,97
и 20 чисел на второй сотне:
101,103,107,109,113,127,131,137,139,149
157,163,167,173,179,181,191,193,197,199

Вывод
Мы РАЗОБРАЛИСЬ, ЧТО ТАКОЕ ОПРЕДЕЛИТЕЛЬ ПРОСТЫХ ЧИСЕЛ («РЕШЕТО Эратосфена»), ПО ЕГО ПРИНЦИПУ СОЗДАЛИ СВОИ ТАБЛИЦЫ и нашли простые числа от 1 до 200, показали, что в одних рядах простых чисел больше, в других- меньше, т.е. встречаются они неравномерно. Но чем дальше мы продвигаемся по числовому ряду, тем реже встречаются простые числа. Возникает вопрос: а существует ли самое последнее простое число?
Древнегреческий математик Евклид (IIIв. До н.э.) в своей книге «Начала», бывшей на протяжении двух тысяч лет основным учебником математики, доказал, что простых чисел бесконечно много, т.е. за каждым простым числом есть ещё большее простое число.
Наша гипотеза оказалась верна, указать самое большое простое число невозможно

Рефлексия
Мне очень понравилось проводить исследования с простыми числами, которые «привлекательны», но в тоже время и неуловимы, я попыталась «уловить», отсеять простые числа от составных пользуясь «Решетом Эратосфена» т.е. проделала работу, которой 2 тыс. лет назад занимался александрийский математик Эратосфен. В дальнейшем я планирую создать таблицы, по которым можно будет проверять делится ли число на 11, 13, 17 и т.д.