Три основные задачи на проценты

1. Нахождение процента от числа
Чтобы найти 0,01p от a, надо a умножить на 0,01p
b=a 0,01p
Чтобы найти процент от числа, надо это число умножить на соответствующую дробь.
Например, 20% от 45 кг равны 45 0.2=9 кг, а 118% от x равны 1.18x.

2. Нахождение числа по его проценту
Чтобы найти число по его части b, выраженной дробью 0,01p, надо b разделить на 0,01p
a=b : 0,01p
Чтобы найти число по его проценту, надо часть, соответствующую этому проценту, разделить на дробь.
Например, 8% длины отрезка составляют 2,4 см, то длина всего отрезка равна 2,4:0,08=30см

3. Нахождение процентного отношения двух чисел
Р = (b:a) 100%
Чтобы найти, сколько процентов число b составляет от a, надо сначала узнать, какую часть b составляет от a, затем эту часть выразить в процентах %.
Чтобы узнать, сколько процентов одно число составляет от второго, надо первое число разделить на второе и результат умножить на 100%.
Например, 9 г соли в растворе массой 180 г составляют (9 100):180=5% раствора.

Решение задач на смеси и сплавы
Таблица для решения задач имеет следующий вид:

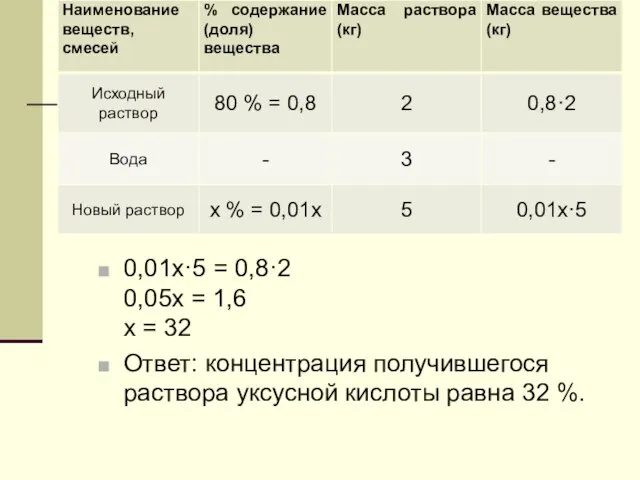
Задача 1. В сосуд содержащий 2 кг 80 % -го водного раствора уксуса добавили 3 кг воды. Найдите концентрацию получившегося раствора уксусной кислоты.
80 %
80 %=0,8
2
0,8·2
3
х % = 0,01х
5
0,01х·5
Масса уксусной кислоты не изменилась

0,01х·5 = 0,8·2
0,05х = 1,6
х = 32
Ответ: концентрация получившегося раствора уксусной кислоты равна 32 %.

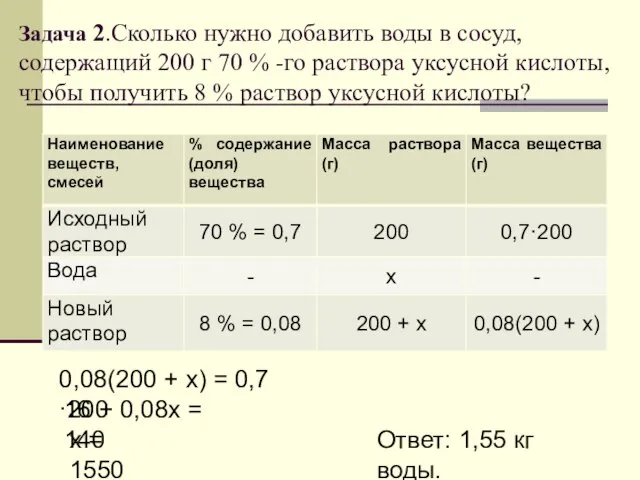
Задача 2.Сколько нужно добавить воды в сосуд, содержащий 200 г 70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?
0,08(200 + х) = 0,7·200
16 + 0,08х = 140
х = 1550
Ответ: 1,55 кг воды.

Задача 3. Смешали некоторое количество 12% раствора соляной кислоты с таким же количеством 20 % раствора этой же кислоты. Найти концентрацию получившейся соляной кислоты.
12 % = 0,12
у
0,12у
20 % = 0,2
у
0,2у
х % = 0,01х
2у
0,01х·2у
0,12у + 0,2у = 0,01х·2у /:у
0,32 = 0,02х
х = 16
Ответ : концентрация
соляной кислоты16%

Задача 4. Смешали 8кг 18 % раствора некоторого вещества с 12 кг 8 % раствора этого же вещества. Найдите концентрацию получившегося раствора.

Задача 4. Смешали 8кг 18 % раствора некоторого вещества с 12 кг 8 % раствора этого же вещества. Найдите концентрацию получившегося раствора.
0,01х·20 = 0,18·8 + 0,08·12
0,2х = 2,4
х = 12
Ответ : концентрация раствора 12 %.

Задача 5 Смешав 40 % и 15 % растворы кислоты, добавили 3 кг чистой воды и получили 20 % раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80 % раствора той же кислоты, то получили бы 50 %-ый раствор кислоты. Сколько килограммов 40 % -го и 15 % растворов кислоты было смешано?
.
0,4х + 0,15у = 0,2(х + у +3)

выполним вторую операцию
Смешав 40 % и 15 % растворы кислоты, добавили 3 кг чистой воды и получили 20 % раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80 % раствора той же кислоты, то получили бы
50 %-ый раствор кислоты. Сколько килограммов 40 % -го и 15 % растворов кислоты было смешано?. 0,4х + 0,15у + 0,8·3 = 0,5(х + у +3).