Содержание
- 2. Понятие ромба Ромб (греч. rhombus) Ромбом называется параллелограмм, у которого все стороны равны. Обладает всеми свойствами
- 3. Этимология Термин «ромб» образован от греч. ρομβος — «бубен». Если сейчас бубны в основном делают круглой
- 4. Свойства Ромб является параллелограммом. Его противолежащие стороны попарно параллельны, АВ || CD, AD || ВС. Диагонали
- 5. Теорема: Диагонали ромба взаимно перпендикулярны и делят его углы пополам Доказать, что: АС ⊥ BD; ∠BAC=
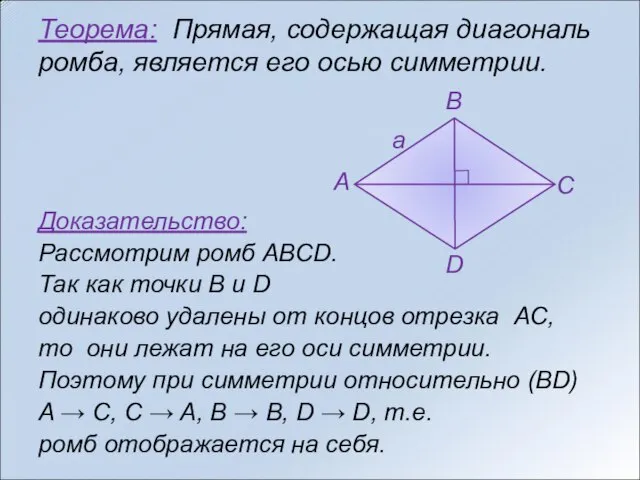
- 6. Теорема: Прямая, содержащая диагональ ромба, является его осью симметрии. Доказательство: Рассмотрим ромб ABCD. Так как точки
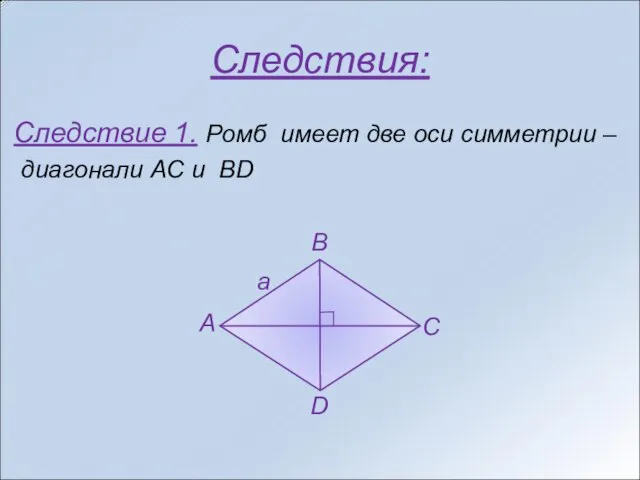
- 7. Следствия: Следствие 1. Ромб имеет две оси симметрии – диагонали AC и BD
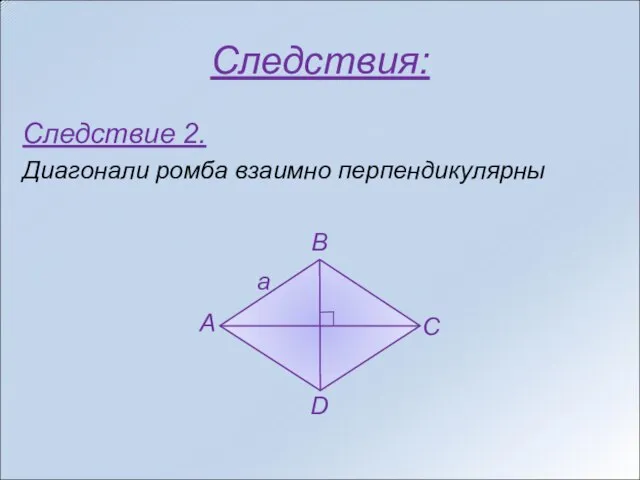
- 8. Следствия: Следствие 2. Диагонали ромба взаимно перпендикулярны
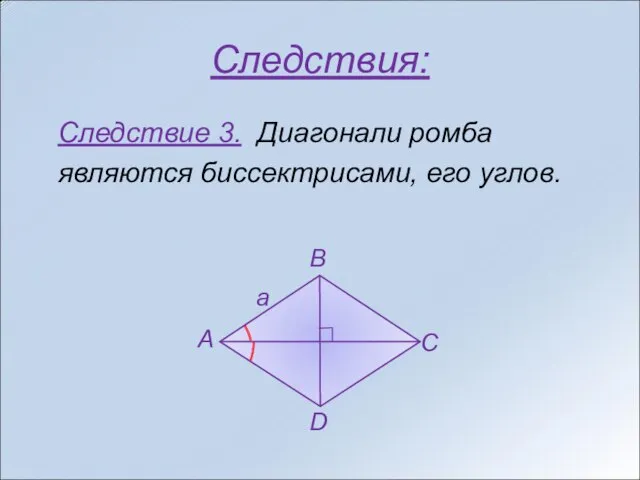
- 9. Следствия: Следствие 3. Диагонали ромба являются биссектрисами, его углов.
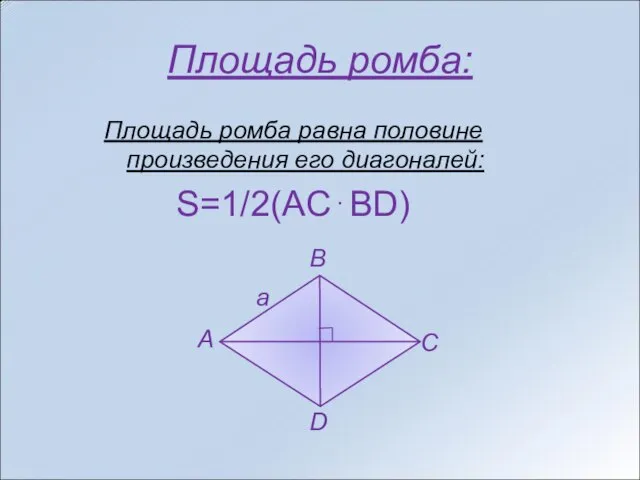
- 10. Площадь ромба: Площадь ромба равна половине произведения его диагоналей: S=1/2(AC⋅BD)
- 11. Площадь ромба Площадь ромба равна половине произведения его диагоналей. Поскольку ромб является параллелограммом, его площадь также
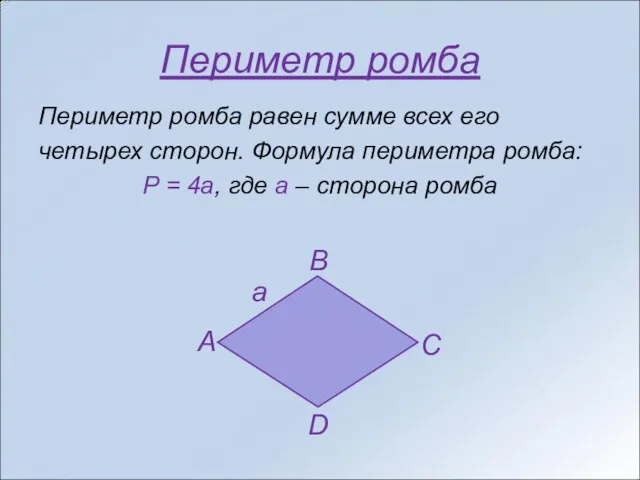
- 12. Периметр ромба Периметр ромба равен сумме всех его четырех сторон. Формула периметра ромба: P = 4a,
- 13. Применение ромба: Ромбические антенны – ионозонды, для изучения параметров ионосферы
- 14. Применение ромба: В вышивке – ромбический орнамент
- 15. Применение ромба: Для украшения посуды
- 16. Применение ромба: При укладке плитки.
- 17. Применение ромба: При укладке плитки
- 19. Скачать презентацию










 Презентация на тему Водные ресурсы. Безопасное использование и охрана
Презентация на тему Водные ресурсы. Безопасное использование и охрана Презентация на тему Физика твердого тела. Рост и дефекты кристаллов
Презентация на тему Физика твердого тела. Рост и дефекты кристаллов
 Презентация на тему Технология моделирования в начальной школе
Презентация на тему Технология моделирования в начальной школе Самостоятельные занятия физическими упражнениями
Самостоятельные занятия физическими упражнениями Права ребёнка
Права ребёнка Риск и промышленная безопасность
Риск и промышленная безопасность  Фрукты, которые растут на деревьях
Фрукты, которые растут на деревьях Какие бывают дома?
Какие бывают дома? Устройство и техническое обслуживание автомобилей классификация грузовых автомобилей
Устройство и техническое обслуживание автомобилей классификация грузовых автомобилей Лес Инвест Трейдинг
Лес Инвест Трейдинг Отцовская доблесть. Семья Канчуриных
Отцовская доблесть. Семья Канчуриных Воздействие тепловых двигателей на окружающую среду
Воздействие тепловых двигателей на окружающую среду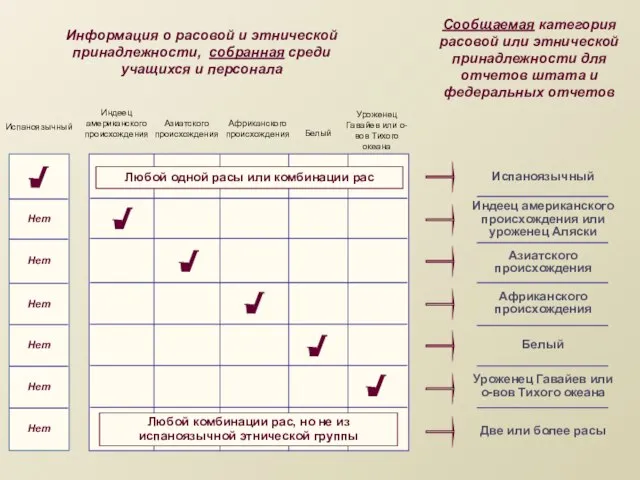 Информация о расовой и этнической принадлежности, собранная среди учащихся и персонала
Информация о расовой и этнической принадлежности, собранная среди учащихся и персонала Бизнес-модель Остервальдера как основной инструмент бизнес-моделирования
Бизнес-модель Остервальдера как основной инструмент бизнес-моделирования Экономия с лампочкой Ilumia Classical
Экономия с лампочкой Ilumia Classical Города РоссииНовосибирск
Города РоссииНовосибирск Решение уравнений высоких степеней
Решение уравнений высоких степеней Слова с сочетаниями ЖИ-ШИ
Слова с сочетаниями ЖИ-ШИ Социальная карта Башкортостана
Социальная карта Башкортостана Викторина
Викторина «Цветок. Строение и функции цветка и его частей»
«Цветок. Строение и функции цветка и его частей» Понятие об общении
Понятие об общении Заочная экскурсия по мемориальному комплексу «ХАТЫНЬ»
Заочная экскурсия по мемориальному комплексу «ХАТЫНЬ» Инструменты автоматизации форматирования. Перекрестные ссылки. Сортировка
Инструменты автоматизации форматирования. Перекрестные ссылки. Сортировка Бюджетная система
Бюджетная система ООО «ЯнаулВодоканал»РБ г. Янаул, ул. Обьездная,17тел. (34760)
ООО «ЯнаулВодоканал»РБ г. Янаул, ул. Обьездная,17тел. (34760) HP StorageWorksX9000 Network Storage Systems
HP StorageWorksX9000 Network Storage Systems Окружность и круг (9 класс)
Окружность и круг (9 класс)