Руководитель Доцент кафедры УМФ СТЕПАНЕЦ Владимир Яковлевич

1. Метод использования путевых координат
Уменьшение объема требуемой памяти может быть достигнуто модификацией основного алгоритма, один из которых и есть метод использования путевых координат.

2. Метод кодирования весов ячеек по модулю 3
К аналогичному сокращению объема информации приводит метод кодирования весов ячеек по модулю 3

3. Метод разметки ДРП по Акерсу
Наиболее экономичный способ кодирования состоя­ний ячеек ДРП предложен Акерсом

4. Метод уменьшения поля поиска
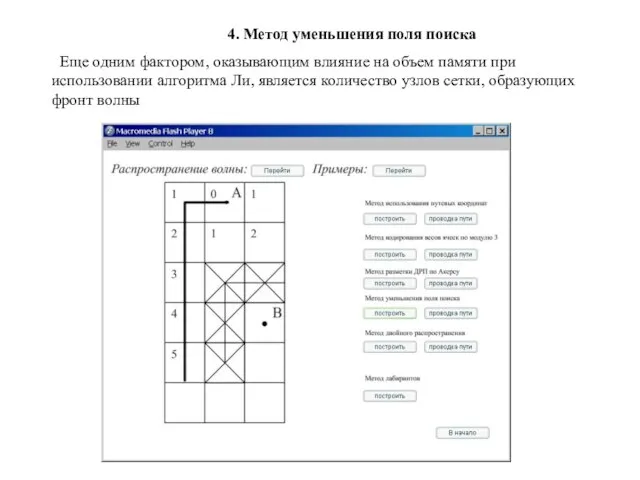
Еще одним фактором, оказывающим влияние на объем памяти при использовании алгоритма Ли, является количество узлов сетки, образующих фронт волны

5. Метод двойного распространения
Если из двух исходных точек (А и В), как из центров, распространяются два фронта, то поле поиска, осуществляемого до момента столкновения двух этих волн, приблизительно в два раза уже, чем при наличии только одной исходной точки

6. Метод с использованием быстрого алгоритма трассировки лабиринтов
Особенностью данного метода поиска является очень высо­кая скорость перемещения в направлении к целевой точке, и поэтому его эффективность в случае сложных лабиринтообразных структур оказывается весьма низкой.

Проведение пути минимальной длины
Задано множество ячеек коммутационного поля, на котором построено некоторое чис­ло проводников. Построить новый проводник между точками А и В так, чтобы он не пересекал ранее построенные про­водники и имел минимально возможную длину.

Проведение пути с минимальным числом изгибов.
Вес незанятой ячейки - го фронта считаем равным весу соседней ячейки - го фронта, если пу­тевая координата в этой ячейке не изменяется, и на единицу больше в противном случае

Проведение пути с минимальным числом пересечений.
При такой постанов­ке задачи занятыми считают ячейки, в которых находятся выводы конструктивных элементов, имеются изгибы или пересечения ранее построенных провод­ников, а также ячейки, в которых направление проводников совпадает с путе­вой координатой строящегося пути

Построение пути, минимально прижимающегося к другим проводникам.
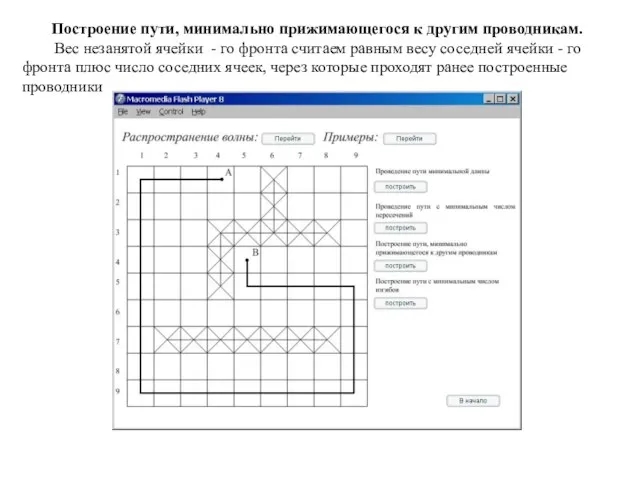
Вес незанятой ячейки - го фронта считаем равным весу соседней ячейки - го фронта плюс число соседних ячеек, через которые проходят ранее построенные проводники

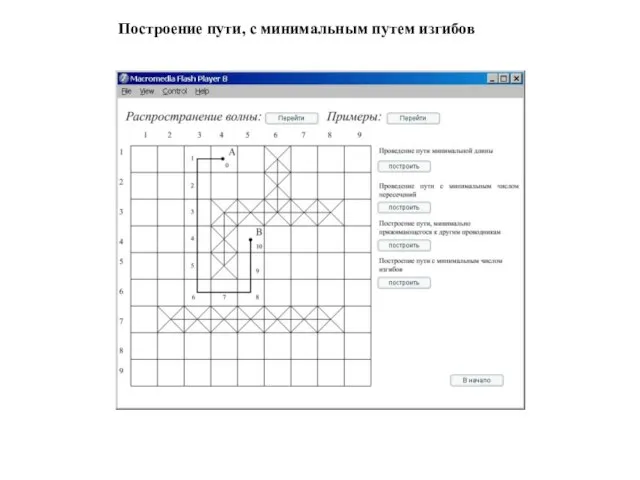
Построение пути, с минимальным путем изгибов

Результаты:
Разработано Электронное пособие по разделу конструирование систем