Содержание
- 2. Данные, используемые в статистическом исследовании, могут быть 2-ух типов: - пространственные; - временные (временные ряды). Одной
- 3. Временной ряд (time series), или ряд динамики – расположенные в хронологической последовательности числовые значения показателя (показателей),
- 4. В каждом ряду динамики выделяют 2 основных элемента: 1) Время (t) – это момент или период
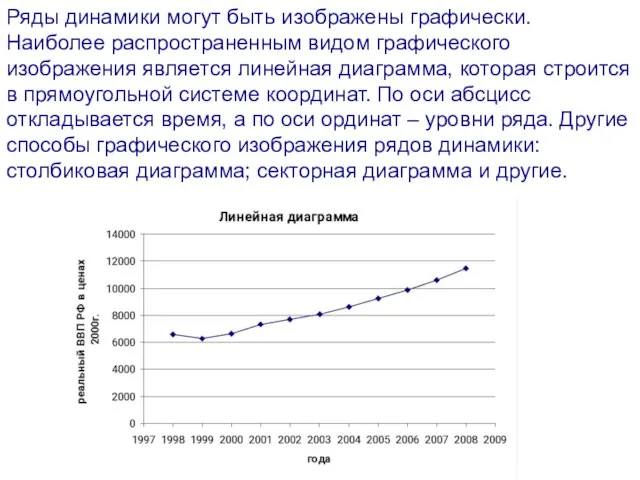
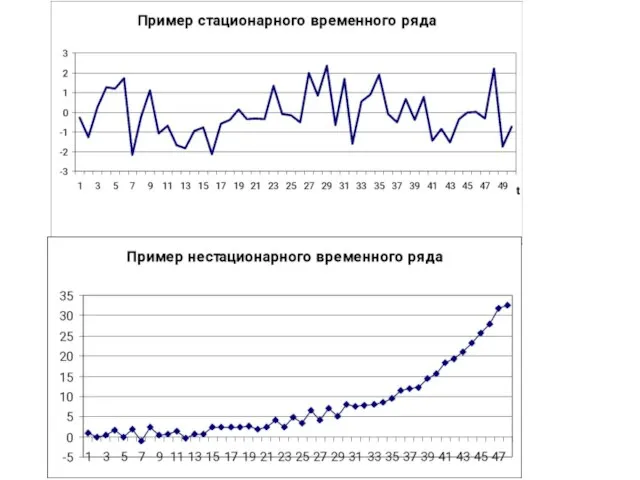
- 5. Ряды динамики могут быть изображены графически. Наиболее распространенным видом графического изображения является линейная диаграмма, которая строится
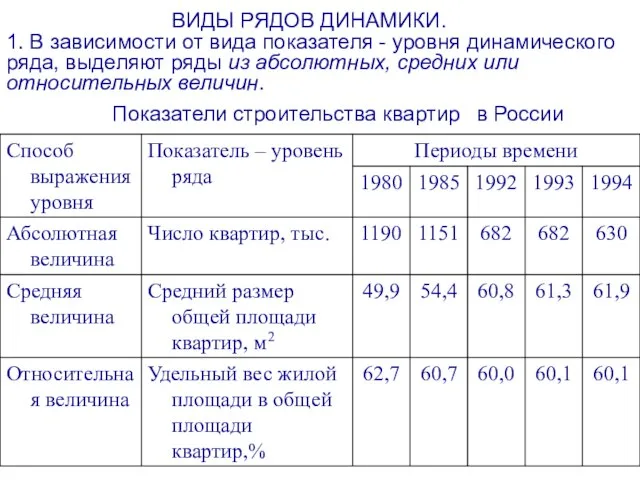
- 6. ВИДЫ РЯДОВ ДИНАМИКИ. 1. В зависимости от вида показателя - уровня динамического ряда, выделяют ряды из
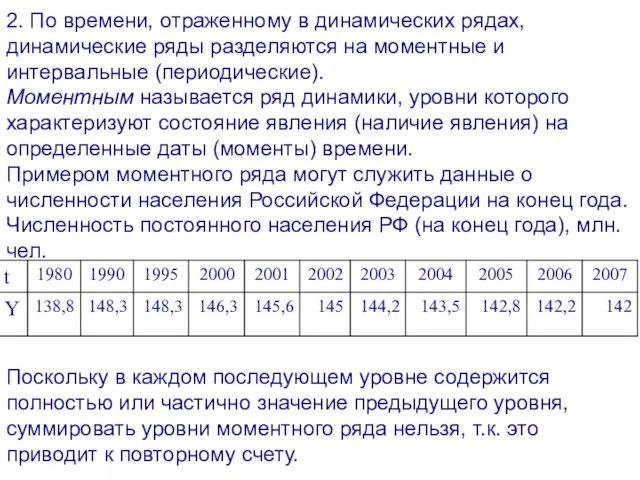
- 7. 2. По времени, отраженному в динамических рядах, динамические ряды разделяются на моментные и интервальные (периодические). Моментным
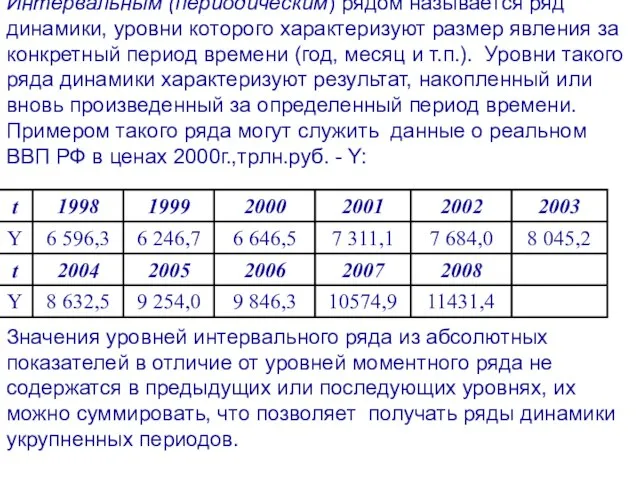
- 8. Интервальным (периодическим) рядом называется ряд динамики, уровни которого характеризуют размер явления за конкретный период времени (год,
- 9. 3. В зависимости от расстояния между уровнями во времени, ряды динамики подразделяются на ряды с равноотстоящими
- 10. 4. Выделяют стационарные и нестационарные ряды динамики. Если математическое ожидание и дисперсия уровня ряда (основные характеристики
- 12. 5. В зависимости от того содержит ряд хронологическую последовательность одного или нескольких показателей - уровней, различают
- 13. СОПОСТАВИМОСТЬ УРОВНЕЙ И СМЫКАНИЕ РЯДОВ ДИНАМИКИ. Важнейшим условием правильного построения ряда динамики является сопоставимость всех входящих
- 14. Под смыканием понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых
- 15. Существует два способа смыкания рядов: 1) пересчет по коэффициенту соотношения уровней 2-х рядов; 2) приведение к
- 16. Согласно второму способу нужно уровень, относящийся к периоду, в котором произошли изменения, принять за 100%, а
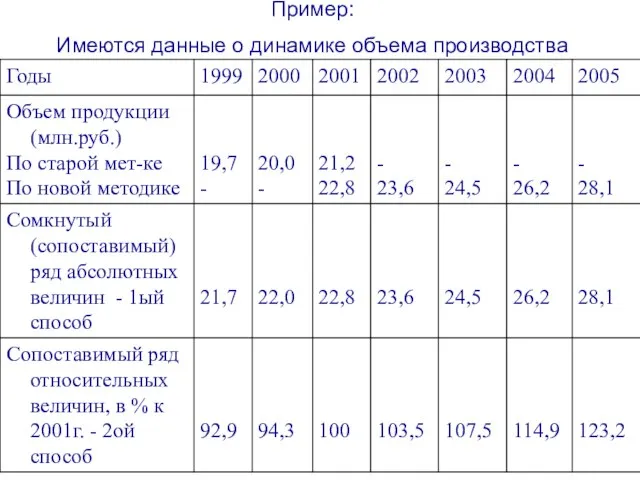
- 17. Пример: Имеются данные о динамике объема производства
- 18. В нашем примере период времени - 2001г. является переходным, т.к. для которого имеются данные об объеме
- 19. В соответствии со вторым способом для условия нашего примера за 100% принимаются уровни 2001г. Уровни 1999-2000гг.
- 20. ПОКАЗАТЕЛИ ИЗМЕНЕНИЯ УРОВНЕЙ РЯДОВ ДИНАМИКИ (ИНДИВИДУАЛЬНЫЕ ПОКАЗАТЕЛИ ДИНАМИКИ) Анализ скорости и интенсивности развития явлений во времени
- 21. Каждому из них соответствует свой временной ряд значений. Длина такого ряда меньше (обычно на единицу) длины
- 22. В зависимости от того, какой уровень берется в качестве базы сравнения, возможны два варианта построения индивидуального
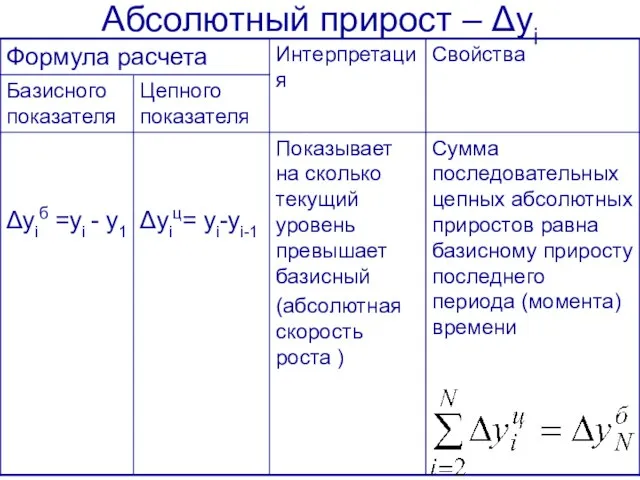
- 23. Абсолютный прирост – Δyi
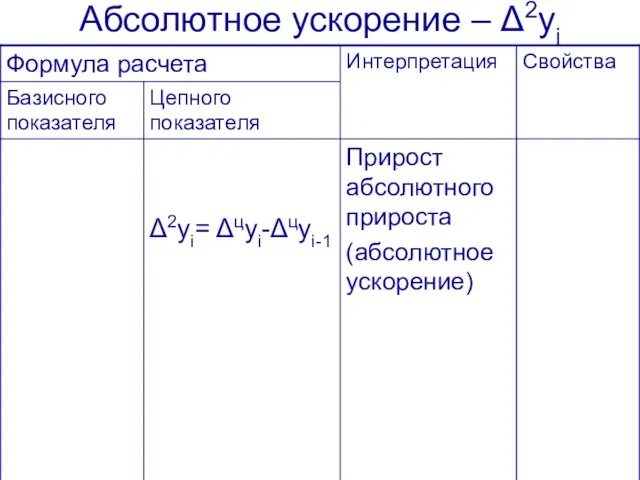
- 24. Абсолютное ускорение – Δ2yi
- 25. Сила роста или коэффициент роста – Kрi
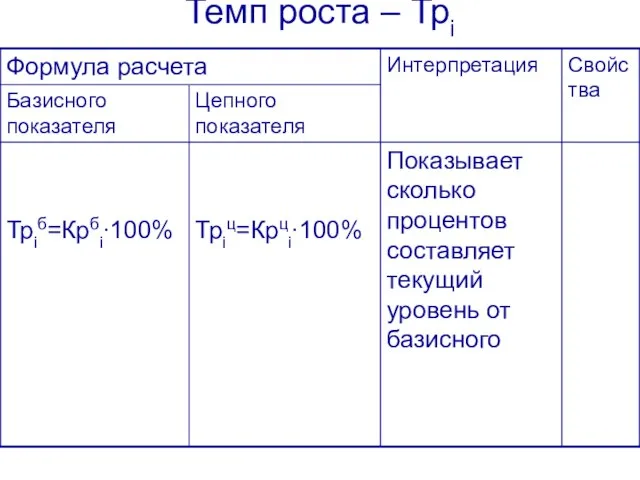
- 26. Темп роста – Трi
- 27. Темп прироста – Тпрi
- 28. Абсолютное значение одного процента прироста – Ai
- 29. Пункт роста – Рi
- 30. Область допустимых значений коэффициента роста и темпа роста от нуля до плюс бесконечности. Область допустимых значений
- 31. СВОДНЫЕ ПОКАЗАТЕЛИ РЯДА ДИНАМИКИ Для обобщающей характеристики динамики исследуемого явления определяют средние показатели динамики: средний уровень
- 32. Средний уровень моментного ряда определяется по формуле среднего хронологического. Для моментных рядов с равноотстоящими уровнями средний
- 33. Средний уровень моментного ряда с неравноотстоящими уровнями определяется по формуле среднего хронологического взвешенного c весами -
- 34. Пример: На основании следующих данных о численности безработных региона -Y, тыс.чел. На 01.01.2005 .................................1,5 На 01.06.2005..................................0,8
- 35. При определении средних уровней временного ряда нужно иметь в виду, что средняя будет достаточно надежной характеристикой
- 36. СРЕДНИЕ ПОКАЗАТЕЛИ ИЗМЕНЕНИЯ УРОВНЕЙ РЯДА Средние показатели изменения уровней ряда рассчитываются усреднением цепных показателей динамики. Средний
- 37. Средний коэффициент роста (сила роста ) - рассчитывается по формуле среднего геометрического из показателей цепных коэффициентов
- 38. Средний темп прироста показывает, на сколько процентов в среднем за единичный промежуток времени изменяется уровень ряда.
- 39. СТРУКТУРА РЯДА ДИНАМИКИ. Уровни ряда динамики формируются под совокупным влиянием множества факторов, различных по характеру и
- 40. 3) Факторов нерегулярного воздействия, вызывающие нерегулярные колебания, которые делятся на: а) спорадически наступающие изменения, вызванные, например,
- 41. Выявление основной тенденции (тренда) или трендового компонента Т называется в статистике выравниванием ряда динамики. При этом
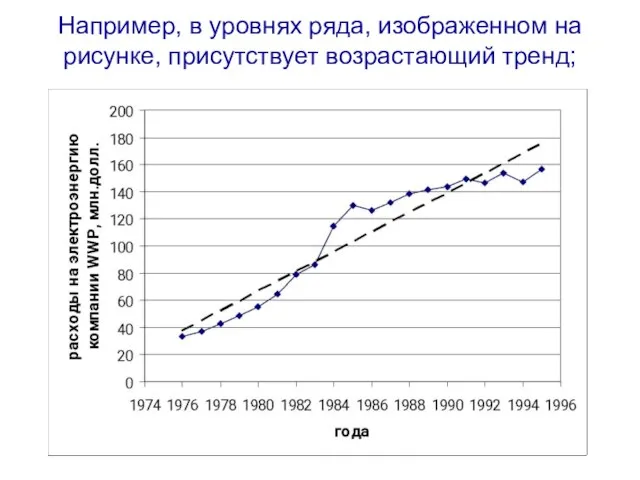
- 42. Например, в уровнях ряда, изображенном на рисунке, присутствует возрастающий тренд;
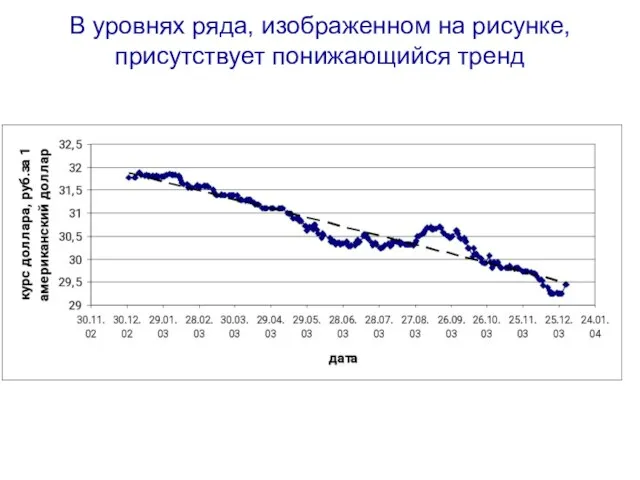
- 43. В уровнях ряда, изображенном на рисунке, присутствует понижающийся тренд
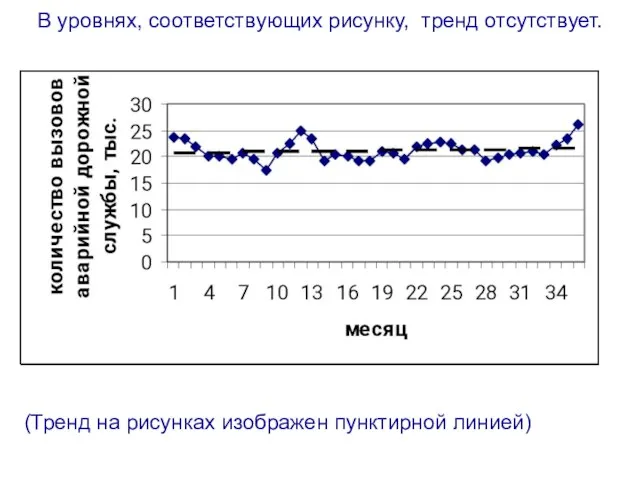
- 44. В уровнях, соответствующих рисунку, тренд отсутствует. (Тренд на рисунках изображен пунктирной линией)
- 45. 1.2) Метод скользящей средней. Суть данного метода состоит в следующем: вычисляется средний уровень из L первых
- 46. Нахождение скользящей средней по четному числу уровней ряда несколько сложнее, так как средняя может быть отнесена
- 47. Проблема выбора интервала сглаживания: при использовании приема скользящей средней сглаженный ряд сокращается по сравнению с исходным
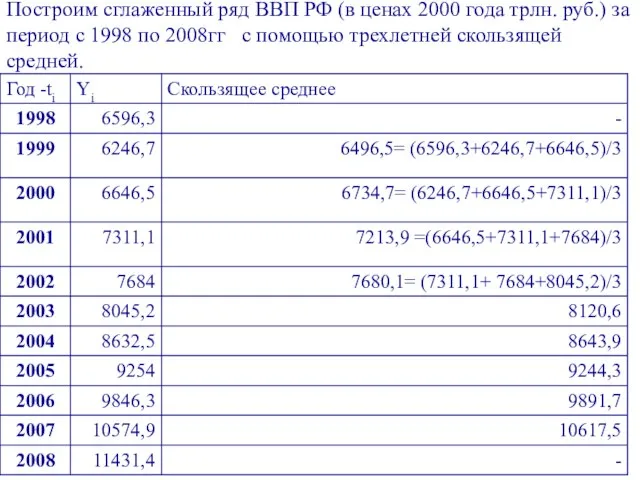
- 48. Построим сглаженный ряд ВВП РФ (в ценах 2000 года трлн. руб.) за период с 1998 по
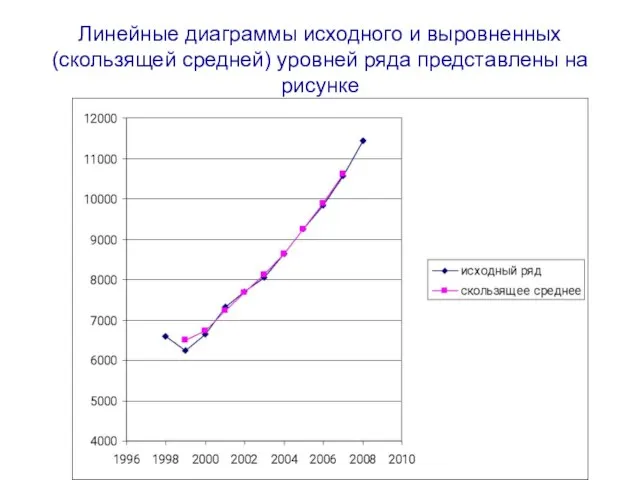
- 49. Линейные диаграммы исходного и выровненных (скользящей средней) уровней ряда представлены на рисунке
- 50. 2) аналитическое выравнивание - наиболее эффективный метод выравнивания. Оно предполагает представление уровней ряда динамики в виде
- 51. Выбор вида функции (f) должен быть основан на содержательном анализе сущности развития данного явления. На практике
- 52. Расчет параметров уравнения тренда. Расчет параметров при аналитическом выравнивании чаще всего производится с помощью метода наименьших
- 53. Поиск параметров для линейного уравнения тренда: f(t) = a+b∙t можно упростить, если отсчет времени производить так,
- 54. При нечетном числе уровней ряда динамики для получения ∑tуi=0 уровень, находящийся в середине ряда, принимается за
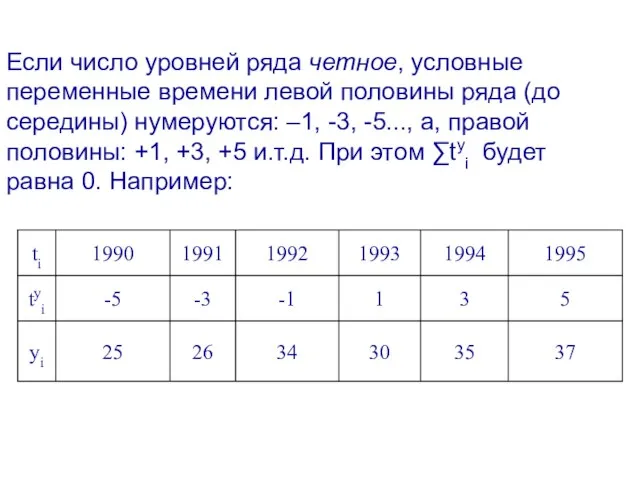
- 55. Если число уровней ряда четное, условные переменные времени левой половины ряда (до середины) нумеруются: –1, -3,
- 56. Система нормальных уравнений (соответствующих МНК) для нахождения параметров линейного уравнения f(tyi) = a+b∙tyi при введении условной
- 57. Оценивание параметров уравнение тренда для показательной функции y =a·bt осуществляется также, как и в случае линейного
- 58. В результате имеем линейное уравнение с новыми переменными и параметрами: z=A+B·t. Для оценки его параметров (A
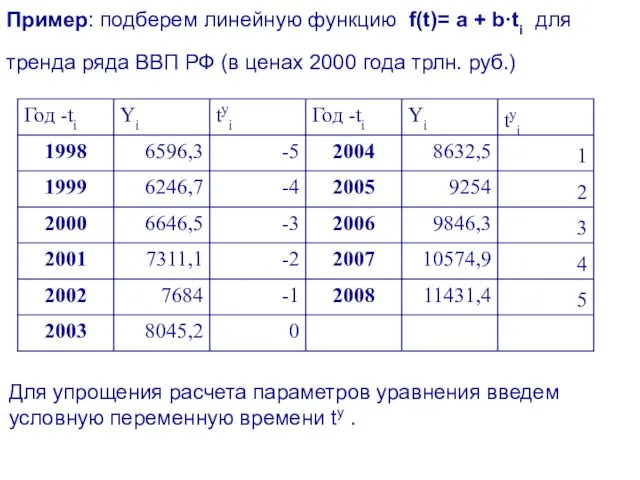
- 59. Пример: подберем линейную функцию f(t)= a + b·ti для тренда ряда ВВП РФ (в ценах 2000
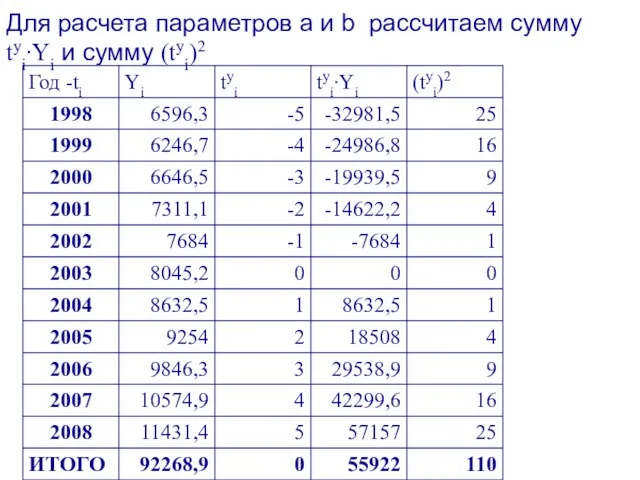
- 60. Для расчета параметров a и b рассчитаем сумму tуi∙Yi и сумму (tуi)2
- 61. Тогда параметры уравнения тренда: f(tу)=a + b∙tу будут равны: Окончательно уравнение примет вид: f(tуi)=8388,1 + 503,4·tуi
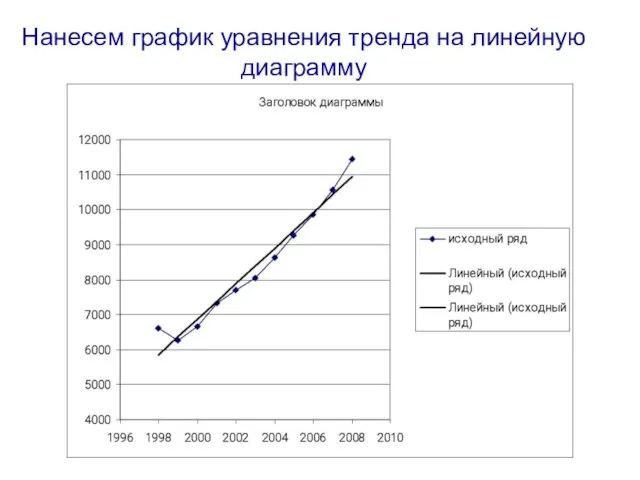
- 62. Нанесем график уравнения тренда на линейную диаграмму
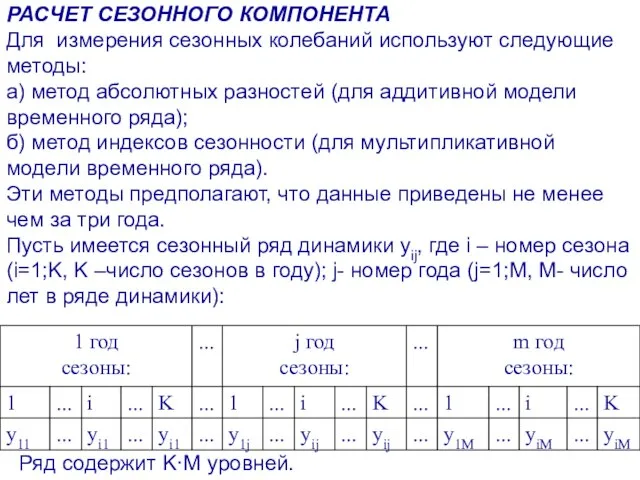
- 63. РАСЧЕТ СЕЗОННОГО КОМПОНЕНТА Для измерения сезонных колебаний используют следующие методы: а) метод абсолютных разностей (для аддитивной
- 64. Метод абсолютных разностей предполагает определение для каждого сезона (месяца, квартала, декады) средней разности между фактическим (yij)
- 65. Индекс сезонности может быть рассчитан разными способами. Для рядов, в которых практически отсутствует повышающийся или понижающийся
- 66. Для рядов динамики с ярко выраженной основной тенденцией, индекс сезонности для i-ого сезона определяется как среднее
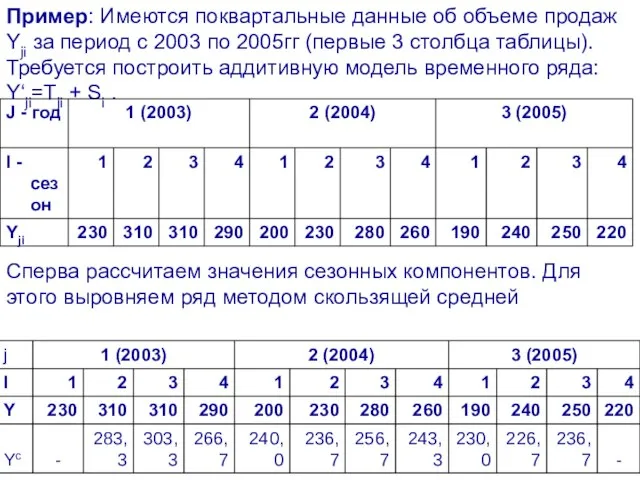
- 67. Пример: Имеются поквартальные данные об объеме продаж Yji за период с 2003 по 2005гг (первые 3
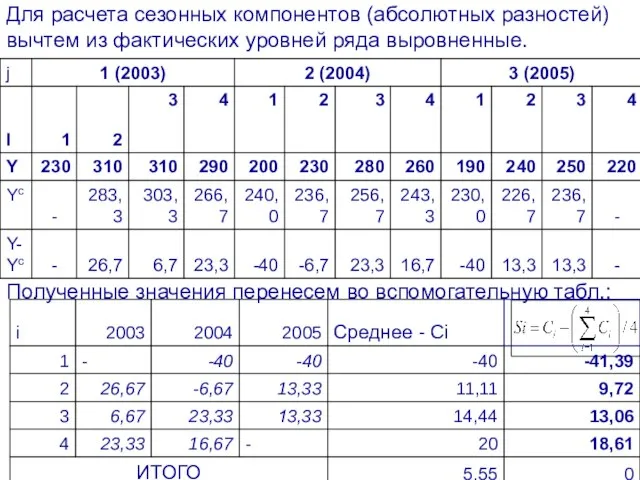
- 68. Для расчета сезонных компонентов (абсолютных разностей) вычтем из фактических уровней ряда выровненные. Полученные значения перенесем во
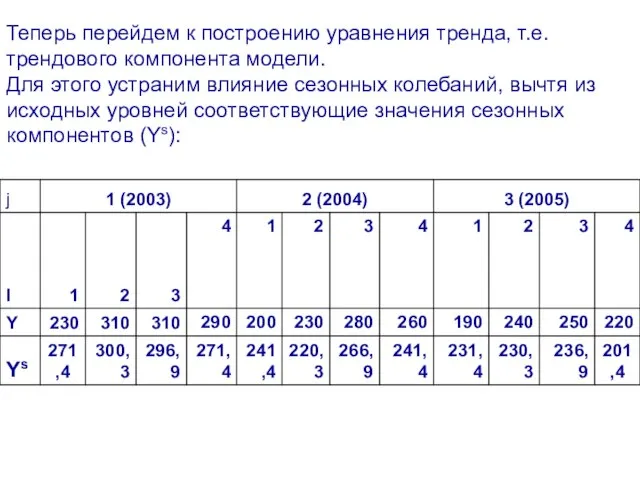
- 69. Теперь перейдем к построению уравнения тренда, т.е. трендового компонента модели. Для этого устраним влияние сезонных колебаний,
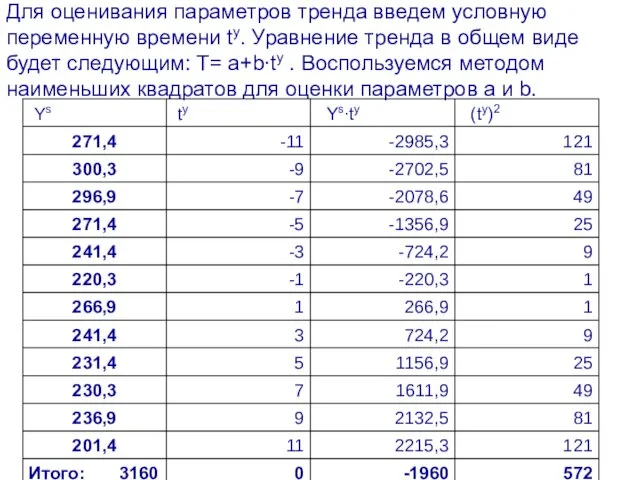
- 70. Для оценивания параметров тренда введем условную переменную времени ty. Уравнение тренда в общем виде будет следующим:
- 71. Уравнение тренда будет следующим: Tji =250,83 – 3,43∙ty Интерпретируем параметры: а= 250,83 показывает средний уровень ряда
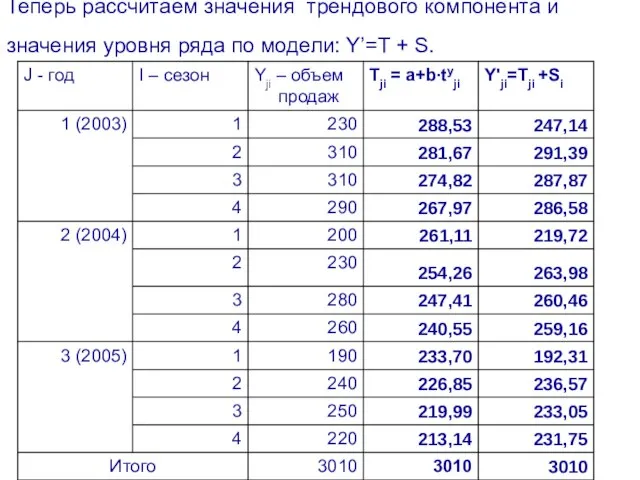
- 72. Теперь рассчитаем значения трендового компонента и значения уровня ряда по модели: Y’=T + S.
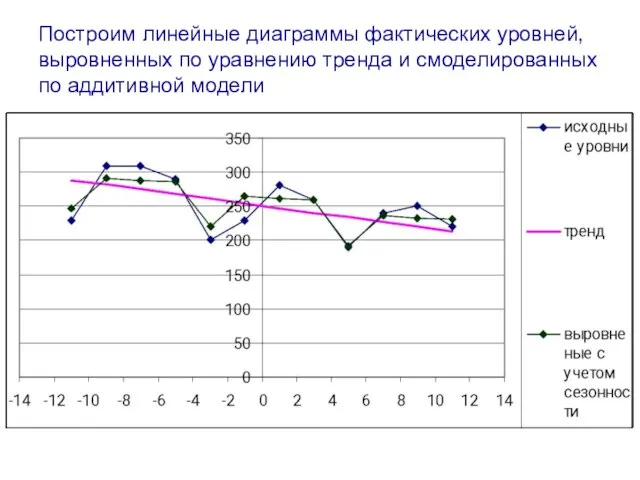
- 73. Построим линейные диаграммы фактических уровней, выровненных по уравнению тренда и смоделированных по аддитивной модели
- 74. СТАТИСТИЧЕСКИЕ МЕТОДЫ ПРОГНОЗИРОВАНИЯ ДИНАМИКИ Обычно рекомендуется, чтобы срок прогноза не превышал 1/3 продолжительности временного ряда. Если
- 75. С помощью аналитического выравнивания (с учетом колеблемости ряда). Методика такого статистического прогноза основана на экстраполяции тренда
- 76. Средняя ошибка прогноза вычисляется по формуле: Где h – число параметров в уравнении тренда,
- 77. Рассмотрим пример: спрогнозируем уровень объема продаж на 1 квартал 2006 г. Для этого определим значение Y’
- 79. Скачать презентацию



















































 Пищевая и легкая промышленность
Пищевая и легкая промышленность Использование лучших мировых практик управления промышленными корпорациями
Использование лучших мировых практик управления промышленными корпорациями Отчет по преддипломной практике в ФГБОУ ВПО Забайкальский государственный университет
Отчет по преддипломной практике в ФГБОУ ВПО Забайкальский государственный университет Famous people of Tatarstan
Famous people of Tatarstan Презентация на тему Леонард Эйлер Идеальный математик XVII века
Презентация на тему Леонард Эйлер Идеальный математик XVII века  Единый государственный экзамен по предметам естественно-математического цикла
Единый государственный экзамен по предметам естественно-математического цикла Продажа земельного участка
Продажа земельного участка Высокоизлучающие покрытия
Высокоизлучающие покрытия БауПрофи*
БауПрофи* Периферическая нервная система
Периферическая нервная система  Внешняя и внутренняя среда организации
Внешняя и внутренняя среда организации Партнерство региональных фондов поддержки малого предпринимательства и кредитных организаций
Партнерство региональных фондов поддержки малого предпринимательства и кредитных организаций Анализ учебных достижений учащихся по результатам выполнения диагностических работ
Анализ учебных достижений учащихся по результатам выполнения диагностических работ Четырехугольники
Четырехугольники Ivebreaker
Ivebreaker  British traditions
British traditions ВОЛОГДА
ВОЛОГДА Оценка памяти младшего школьника. Диагностика познавательного развития
Оценка памяти младшего школьника. Диагностика познавательного развития Музыкально - ритмические движения
Музыкально - ритмические движения Презентация на тему Клизмы
Презентация на тему Клизмы  20141103_issledovateli_dalnego_vostoka
20141103_issledovateli_dalnego_vostoka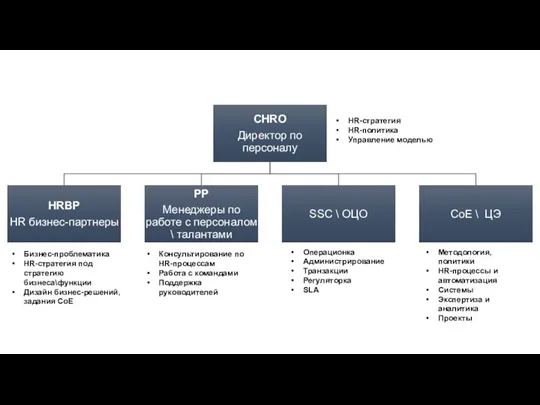 CHRO. Директор по персоналу
CHRO. Директор по персоналу Презентация на тему Природа Тундры
Презентация на тему Природа Тундры Гусевский хрусталь
Гусевский хрусталь Синтетическая природа фильма и монтаж. Пространство и время в кино
Синтетическая природа фильма и монтаж. Пространство и время в кино Жизнь и чудеса Иисуса Христа
Жизнь и чудеса Иисуса Христа Интерактивная выставка-презентация Финансы России: время первых (II этап)
Интерактивная выставка-презентация Финансы России: время первых (II этап) Что такое орнамент
Что такое орнамент