Содержание
- 2. Выгорание кластеров
- 3. Выгорание кластеров
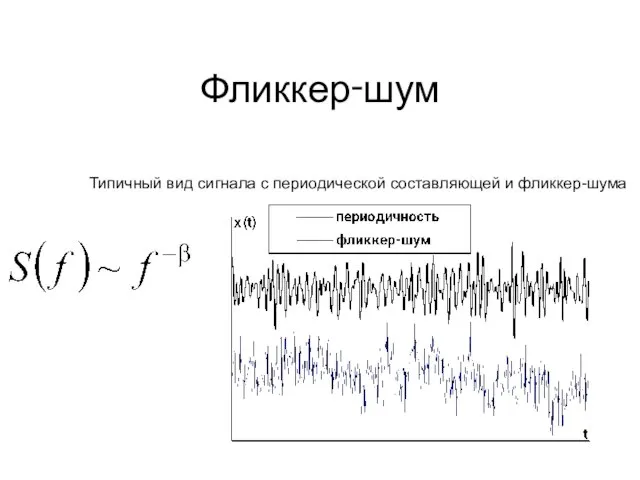
- 4. Фликкер‑шум Типичный вид сигнала с периодической составляющей и фликкер-шума
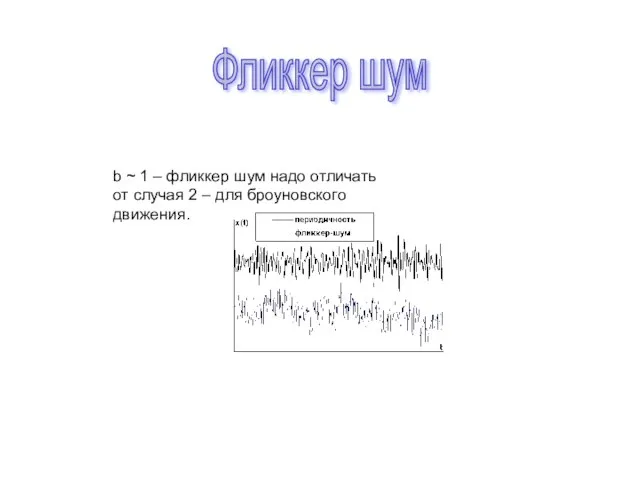
- 5. b ~ 1 – фликкер шум надо отличать от случая 2 – для броуновского движения. Фликкер
- 6. Степенные распределения В качестве классического примера можно привести закон Рихтера–Гутенберга: зависимость количества землетрясений от их энергии
- 7. Разница между нормальным и степенным распределениями носит не формальный, а принципиальный характер. Если статистика системы описывается
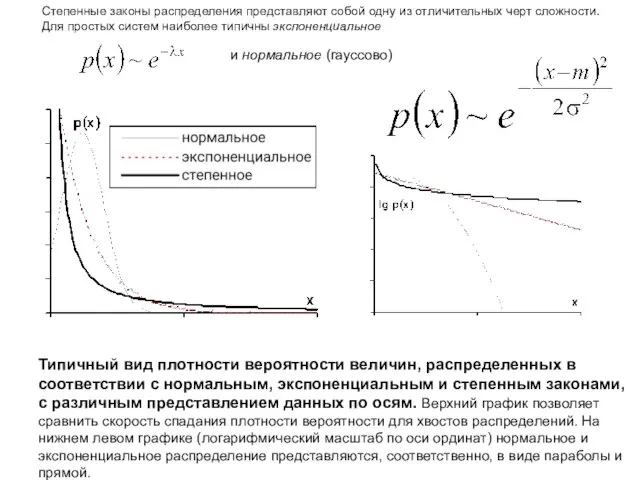
- 8. Степенные законы распределения представляют собой одну из отличительных черт сложности. Для простых систем наиболее типичны экспоненциальное
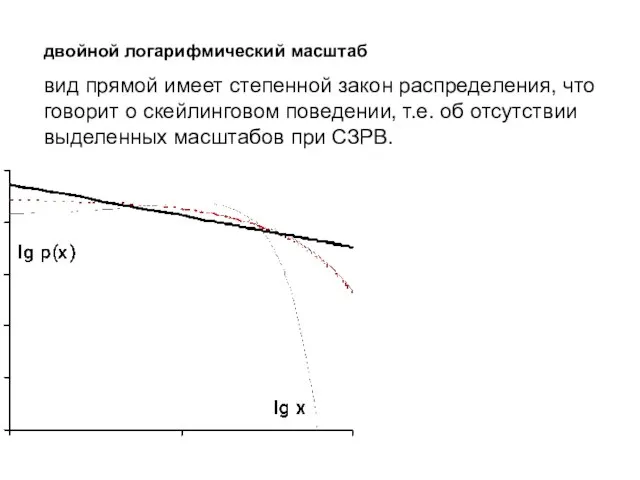
- 9. двойной логарифмический масштаб вид прямой имеет степенной закон распределения, что говорит о скейлинговом поведении, т.е. об
- 10. Процесс смерти и размножения. единичное значение коэффициента размножения соответствует критическому ветвящемуся процессу, описываемому формулой заразившийся человек
- 11. Устойчивые законы распределения
- 12. Устойчивые законы распределения
- 13. Устойчивые законы распределения g' зависит от b, g и a, причем g' = g, если a
- 14. Степенные распределения a управляет асимптотикой распределения и может принимать значения в интервале 0 при a .
- 15. Таким образом, распределения с тяжелыми хвостами являются не альтернативой нормального распределения, а его естественным дополнением. Если
- 16. Случай a Случай a для которого bn = n, и если выбрать g = 0, то
- 17. Случай a Случай a для которого bn = n, и если выбрать g = 0, то
- 18. Очевидно, что нормировка будет еще больше для меньших значений a. Например, для распределения Леви bn =
- 19. , т.е. в сумму случайных величин, распределение которых имеет хвост вида (2) с a bn =
- 20. Если слагаемые имеют конечную дисперсию, то в силу центральной предельной теоремы предельное распределение будет нормальным, что
- 21. Энергия землетрясения E пропорциональна произведению площади разлома S и смещения пластов DL. Для не очень сильных
- 22. Малые землетрясения. откуда в силу формул (7) и (9) немедленно получаем для энергии устойчивое распределение с
- 23. Большие землетрясения. откуда в силу формул (7) и (9) немедленно получаем для энергии устойчивое распределение с
- 24. где скейлинговая f(y) приблизительно постоянна при y ~ 1 и быстро убывает при y → ∞.
- 32. Фликкер-шум явление фликкер-шума обусловлено отсутствием характерных времен, т.е. степенным распределением временных характеристик процессов. Поясним это рассуждение
- 33. Спектр мощности S(f) любого процесса представляет собой просто преобразование Фурье от его автокорреляции которая дается формулой
- 34. Если воспользоваться временной разнесенностью событий рассматриваемого процесса и пренебречь взаимодействием между ними, то для автокорреляции (
- 36. Скачать презентацию

















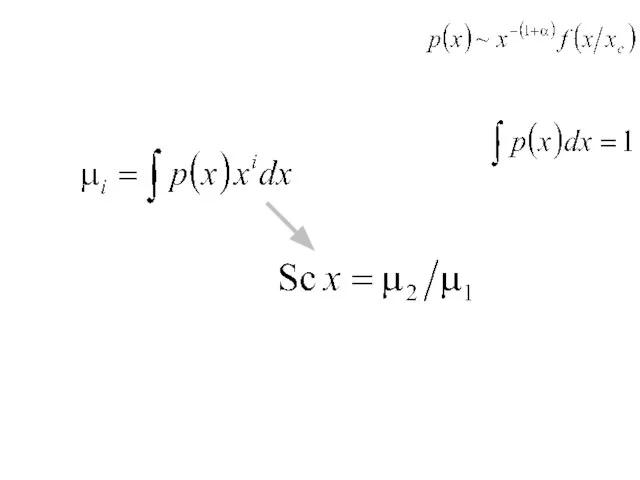









 Современные возможности пробиотической терапии в клинике внутренних болезней
Современные возможности пробиотической терапии в клинике внутренних болезней Территория смыслов
Территория смыслов Карта пробных ароматов: Al Haramain/Aysha (милая)
Карта пробных ароматов: Al Haramain/Aysha (милая) Понятие мониторинга
Понятие мониторинга Прием письменного вычитания в случаях вида 50-24
Прием письменного вычитания в случаях вида 50-24 Акварельные зарисовки
Акварельные зарисовки Русские народные сказки
Русские народные сказки Красная книга растений
Красная книга растений Биография. Шаблон
Биография. Шаблон Дифференциальная диагностика и принципы лечения синдрома Корнелии Де ЛАНГЕ
Дифференциальная диагностика и принципы лечения синдрома Корнелии Де ЛАНГЕ Презентация на тему Телескоп
Презентация на тему Телескоп Презентация Сушильникова Н.И. Экологическая сказка
Презентация Сушильникова Н.И. Экологическая сказка Телеметрическая платформа M2MGate Solution
Телеметрическая платформа M2MGate Solution Китайский клуб МИИТа
Китайский клуб МИИТа Тема выпускной квалификационной работы. Шаблон
Тема выпускной квалификационной работы. Шаблон Морской порт Санкт-Петербург. Отчет по результатам линейного обхода
Морской порт Санкт-Петербург. Отчет по результатам линейного обхода С днем рождения!!!
С днем рождения!!! Муниципальное дошкольное образовательное учреждение «Детский сад № 15» г. Чебоксары
Муниципальное дошкольное образовательное учреждение «Детский сад № 15» г. Чебоксары Презентация на тему Климат Африки
Презентация на тему Климат Африки Коммуникативный практикум
Коммуникативный практикум Государство. Понятие. Теории происхождения
Государство. Понятие. Теории происхождения Жизнь прекрасна
Жизнь прекрасна Измерение расхода. FR — лидер в новейшей высокоточной технологии измерения расхода
Измерение расхода. FR — лидер в новейшей высокоточной технологии измерения расхода Венев
Венев ПУТЕШЕСТВИЕ ПО МАТЕРИКАМ
ПУТЕШЕСТВИЕ ПО МАТЕРИКАМ Экономия водоснабжения
Экономия водоснабжения Рифмоплёт
Рифмоплёт Вареники с картошкой
Вареники с картошкой