Санкт-Петербургский государственный университетинформационных технологий, механики и оптики

А.В.Павлов Инт. Инф. Сист
Мозг здорового бодрствующего человека является предельно неустойчивой хаотической системой.
Без хаотической динамики невозможно обучение – мозг не может добавить в память новый образ
[Фриман Дж.У., Динамика мозга в восприятии и сознании: творческая роль хаоса // В сб. «Синергетика и психология». Вып.3. "Когнитивные процессы", Издательство «Когито-Центр", 2004.].

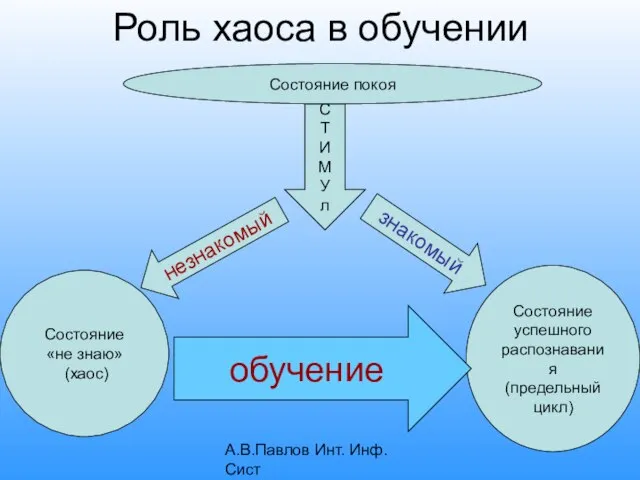
А.В.Павлов Инт. Инф. Сист
Роль хаоса в обучении
Состояние покоя
С
Т
И
М
У
л
незнакомый
Состояние
«не знаю»
(хаос)
знакомый
Состояние
успешного
распознавания
(предельный цикл)
обучение

А.В.Павлов Инт. Инф. Сист
Три типа динамики – три типа аттракторов
Устойчивая система –аттрактор с единственным глобальным минимумом, конвергентная динамика;
Предельный цикл – циклическая динамика;
Хаос – странный аттрактор.

А.В.Павлов Инт. Инф. Сист
Итерирующее отображение
(X,d) – метрическое пространство
T:X→X сжимающее отображение, если
∃S, 0
Если S∈(0,∞), то Т – отображение Липшица.
Теорема о сходимости к неподвижной точке.
(X,d), T – сжимающее отображение, xf – неподвижная точка, т.е. T(xf)=xf,
T(x) имеет в конечном счете одну неподвижную точку и, кроме того,
∀x0∈X, , где xn = T(xn-1).
xn
Xn+1
x0
Паутинная диаграмма

А.В.Павлов Инт. Инф. Сист
Свойство единственности неподвижной точки
Пусть T(x) имеет две неподвижные точки xf1 и xf2.
Тогда по определению сжимающего отображения
d(T(xf1),T(xf2))=d(T(xf1),T(xf2))≤Sd(xf1,xf2),
Так как S<1, то последнее неравенство выполняется только при xf1 = xf2.

А.В.Павлов Инт. Инф. Сист
Притягивающие и отталкивающие точки.
Отображение f не предполагается сжимающим, ⇒ теорема о неподвижной точке неприменима. Xf – неподвижная точка.
Разложим f в ряд Тейлора вблизи неподвижной точки
f(x) = f(xf)+(x-xf)(f’(x)).
По определению неподвижной точки f(xf)=xf, то следующий шаг
xn+1=f(xn) ⇒ xn+1-xn=(xn-xf)f’(xf)
если ⏐f’(xf)⏐>1, то xf - отталкивающая, т.к. с каждым шагом расстояние увеличивается, орбиты из ее окрестности расходятся;
если ⏐f’(xf)⏐<1, то xf - притягивающая, т.к. с каждым шагом расстояние уменьшается, орбиты из ее окрестности сходятся.

А.В.Павлов Инт. Инф. Сист
Периодические точки
Точки ξ1 и ξ2 : f(ξ1)= ξ2; f(ξ2)= ξ1;
Def. Последовательность
называется орбитой точки x0.
Def. Орбита называется периодической с периодом р, если xn+p=xn; n=0,1,2…
Если условие периодичности xn+p=xn справедливо только после некоторого n≥n0, то орбита в конечном счете периодическая.

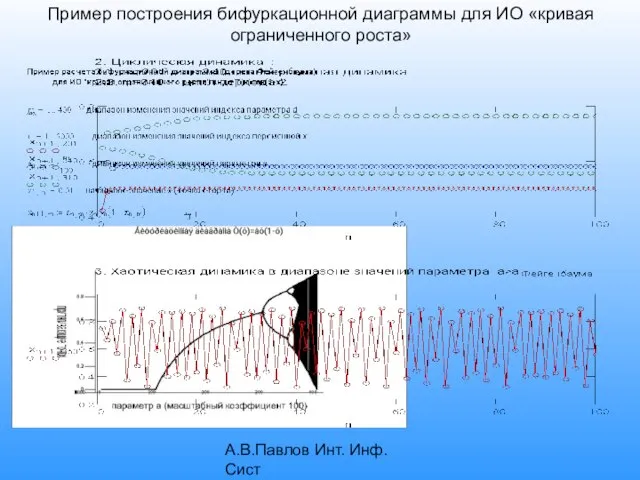
А.В.Павлов Инт. Инф. Сист
Примеры итерирующих отображений, приводящих к хаосу
модель ограниченного роста T: xn+1=axn(1-xn) (Верхольст, 1845)
xn+1=xn2+a
xn+1=xn(1+a (1-xn))
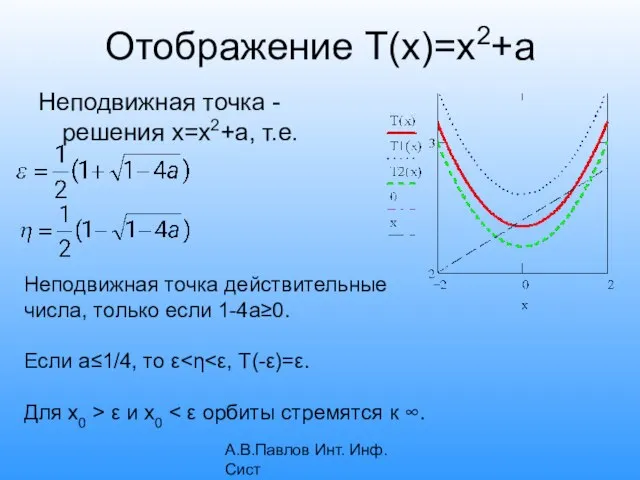
xn+1=xn exp(a(1-xn))

А.В.Павлов Инт. Инф. Сист
Отображение T(x)=x2+a
Неподвижная точка - решения x=x2+a, т.е.
Неподвижная точка действительные числа, только если 1-4а≥0.
Если а≤1/4, то ε<η<ε, T(-ε)=ε.
Для x0 > ε и x0 < ε орбиты стремятся к ∞.

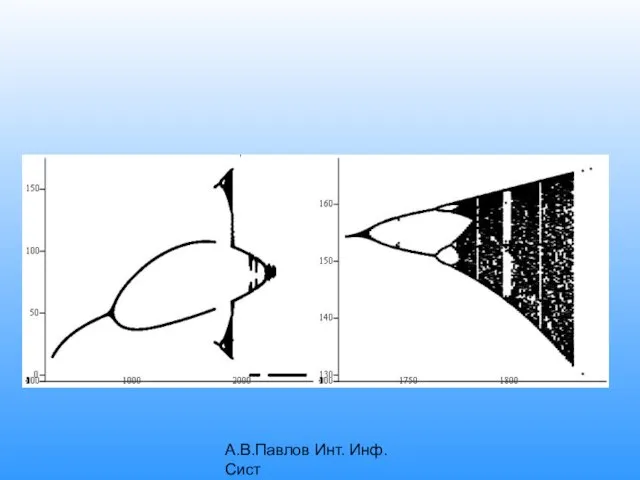
А.В.Павлов Инт. Инф. Сист
Пусть I≡[-ε,ε], если -2≤а≤1/4 и x0∈I, то T(x0)∈I.
–3/4 ⇒ ⏐T’(η)⏐=⏐1-(1-4a)1/2⏐<1 ⇒ Неподвижная точка притягивающая все орбиты с x0∈I сходятся к η.
T(x)=x2+a

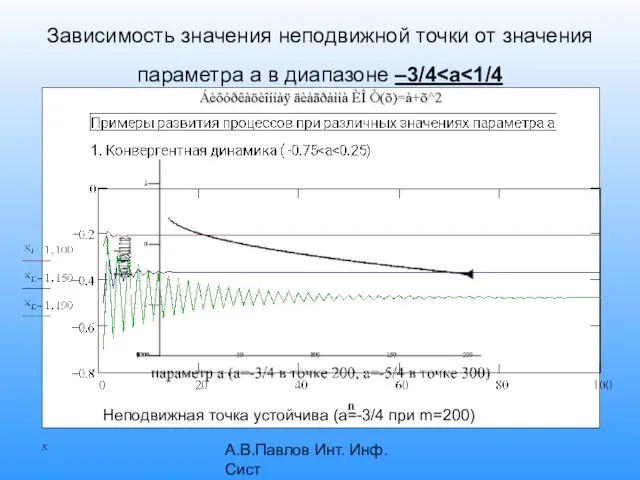
А.В.Павлов Инт. Инф. Сист
Зависимость значения неподвижной точки от значения параметра а в диапазоне –3/4
Неподвижная точка устойчива (а=-3/4 при m=200)

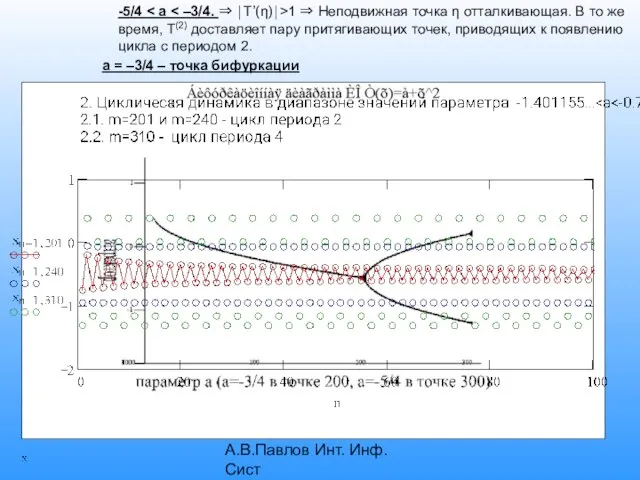
А.В.Павлов Инт. Инф. Сист
-5/4 < a < –3/4. ⇒ ⏐T’(η)⏐>1 ⇒ Неподвижная точка η отталкивающая. В то же время, T(2) доставляет пару притягивающих точек, приводящих к появлению цикла с периодом 2.
a = –3/4 – точка бифуркации

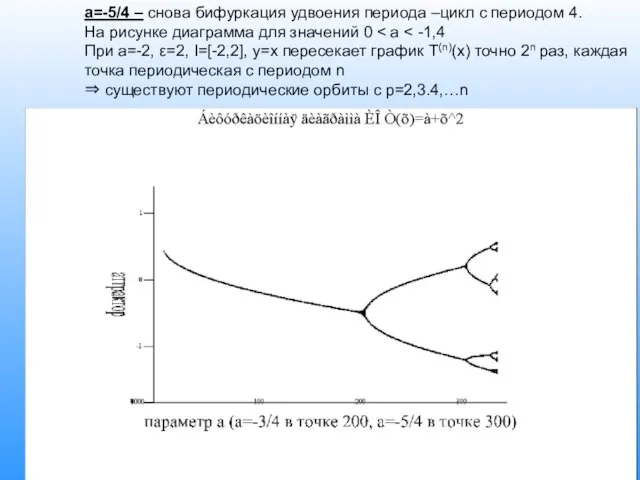
А.В.Павлов Инт. Инф. Сист
a=-5/4 – снова бифуркация удвоения периода –цикл с периодом 4.
На рисунке диаграмма для значений 0 < а < -1,4
При а=-2, ε=2, I=[-2,2], y=x пересекает график Т(n)(x) точно 2n раз, каждая точка периодическая с периодом n
⇒ существуют периодические орбиты с р=2,3.4,…n

А.В.Павлов Инт. Инф. Сист

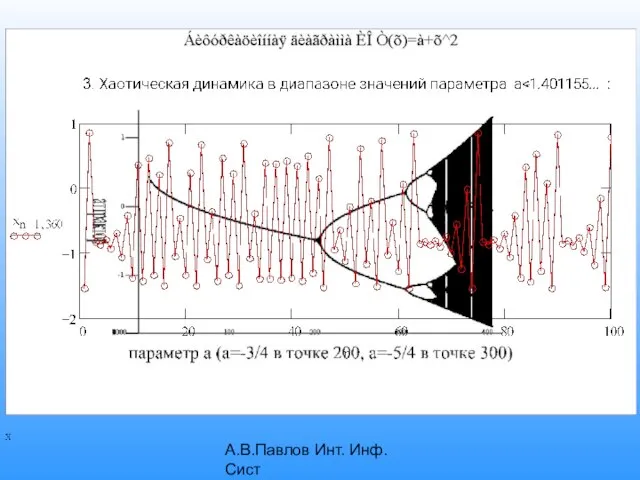
А.В.Павлов Инт. Инф. Сист
Точка Фейгенбаума
a∞=liman=-1.401155…., где an – значения точек бифуркаций.
¼ удвоение периода
a∞
в окрестности а=-1.7548777… - окно периода 3.
Отношение длин интервалов между точками бифуркаций имеет предел
постоянная Фейгенбаума.
Если значения а∞ для разных ф-ций разные, то значение d одно для очень многих ф-ций.

А.В.Павлов Инт. Инф. Сист
Пример построения бифуркационной диаграммы для ИО «кривая ограниченного роста»

А.В.Павлов Инт. Инф. Сист
Определение хаоса
Пусть (X,d) метрическое пространство. Отображение T:X→X называется хаотическим, если:
Т обладает существенной зависимостью от начальных условий, а именно: (X,d), x∈X, U – открытое мн-во, x∈U, для δ>0 ∃n>0 и (⋅)y∈U, что d(T(n)(x),T(n)y))>δ;
2. Т транзитивно, т.е. для ∀U,V – открытых мн-в ∃n≥0 такое, что T(n)(U)∧V≠∅;
3. Периодические точки плотны в Х, т.е. в любой окрестности ∀ точки в Х существует по крайней мере одна периодическая точка и, следовательно, бесконечное множество периодических точек.
Это – строгий хаос. Строго говоря, условие (1) избыточно, т.к. оно следует из 2 и 3.

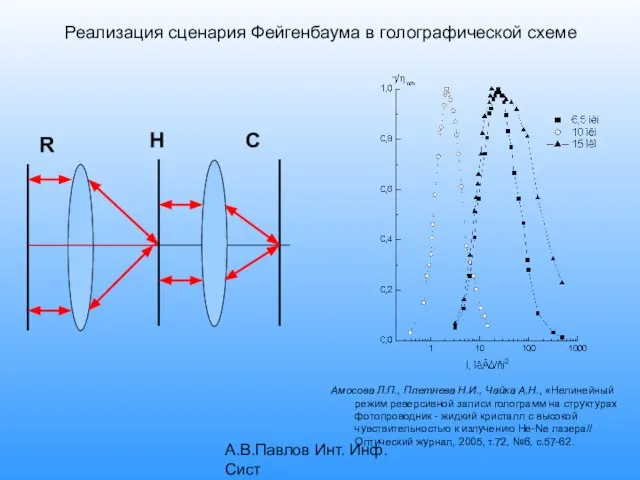
А.В.Павлов Инт. Инф. Сист
Реализация сценария Фейгенбаума в голографической схеме
Амосова Л.П., Плетнева Н.И., Чайка А.Н., «Нелинейный режим реверсивной записи голограмм на структурах фотопроводник - жидкий кристалл с высокой чувствительностью к излучению He-Ne лазера// Оптический журнал, 2005, т.72, №6, с.57-62.

А.В.Павлов Инт. Инф. Сист
Сходимость процесса в зависимости от точки старта

А.В.Павлов Инт. Инф. Сист