Содержание
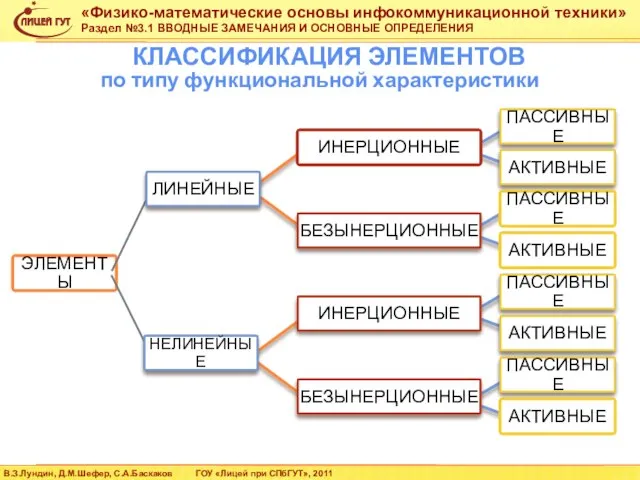
- 4. КЛАССИФИКАЦИЯ ЭЛЕМЕНТОВ по типу функциональной характеристики
- 5. Иллюстрации типовых свойств элементов и ФУ Линейность и нелинейность Линейный элемент (узел, устройство) в отличие от
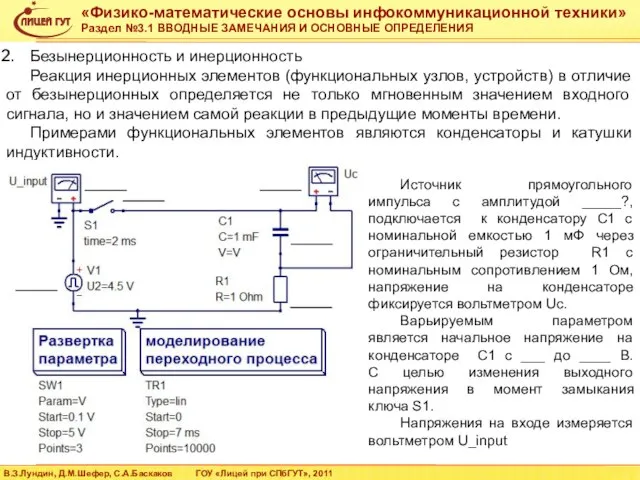
- 8. Безынерционность и инерционность Реакция инерционных элементов (функциональных узлов, устройств) в отличие от безынерционных определяется не только
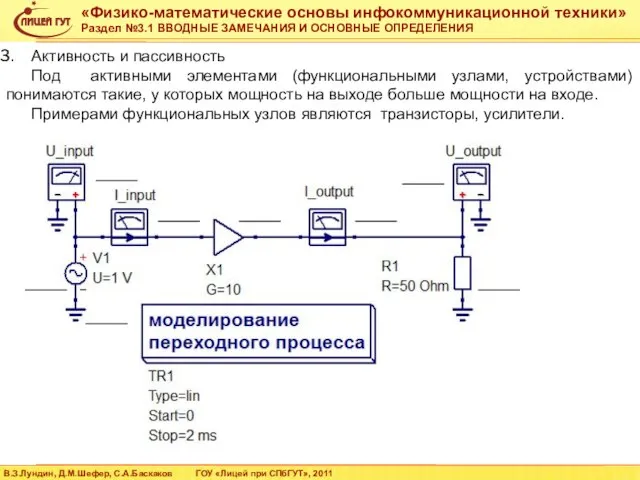
- 9. Активность и пассивность Под активными элементами (функциональными узлами, устройствами) понимаются такие, у которых мощность на выходе
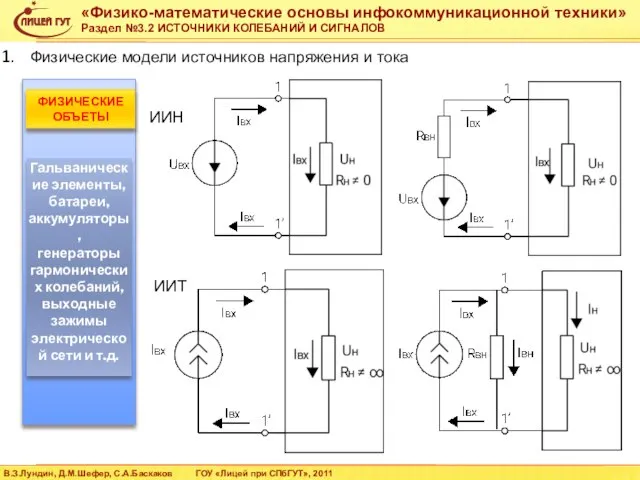
- 12. ИИН ИИТ Физические модели источников напряжения и тока
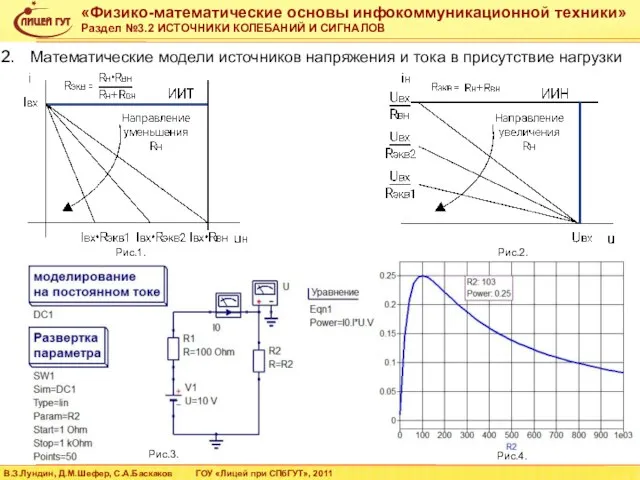
- 13. Математические модели источников напряжения и тока в присутствие нагрузки Рис.1. Рис.2. Рис.3. Рис.4.
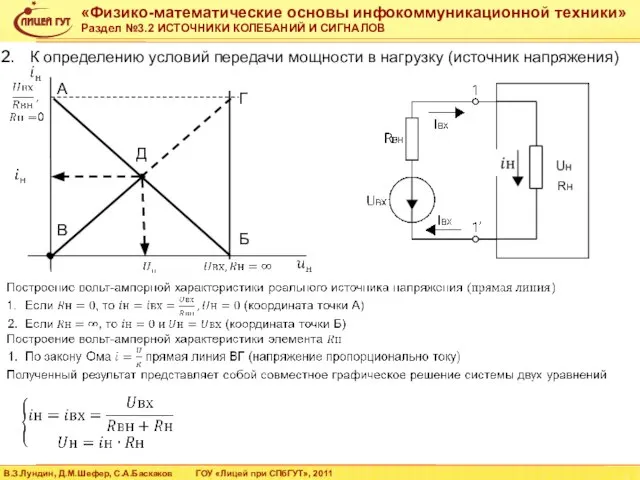
- 14. К определению условий передачи мощности в нагрузку (источник напряжения) А Б В Г Д Rн
- 15. Аналитический вывод условия максимальной передачи мощности Тогда мощность, выделяющаяся на нагрузке равна:
- 18. Рези́стор (англ. resistor, от лат. resisto — сопротивляюсь) – элемент, основным свойством которого является перевод электрической
- 19. Номиналы сопротивлений промышленно выпускаемых резисторов не являются произвольными. Существуют специальные ряды номиналов, представляющие собой множества значений
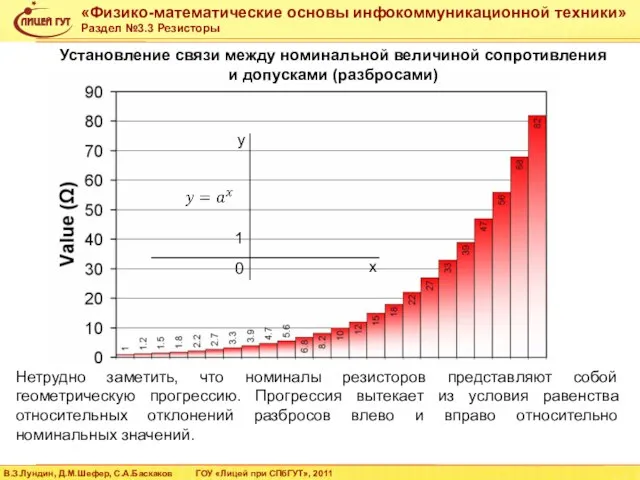
- 20. Установление связи между номинальной величиной сопротивления и допусками (разбросами) Нетрудно заметить, что номиналы резисторов представляют собой
- 21. Это делает возможным путем решения показательного уравнения определить, как количество номиналов в декаде, так и их
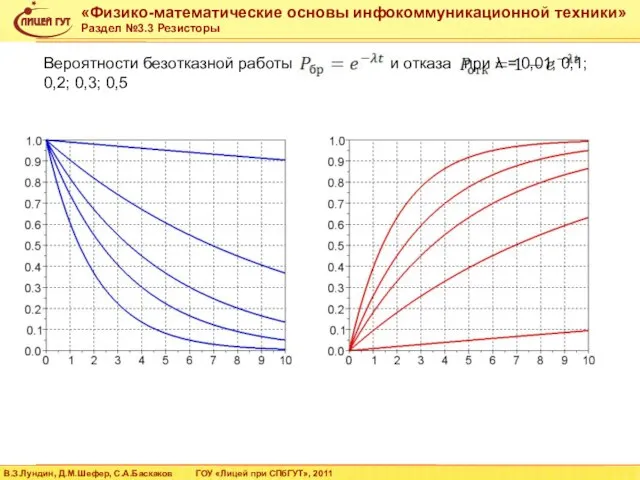
- 23. Вероятности безотказной работы и отказа при λ = 0,01; 0,1; 0,2; 0,3; 0,5
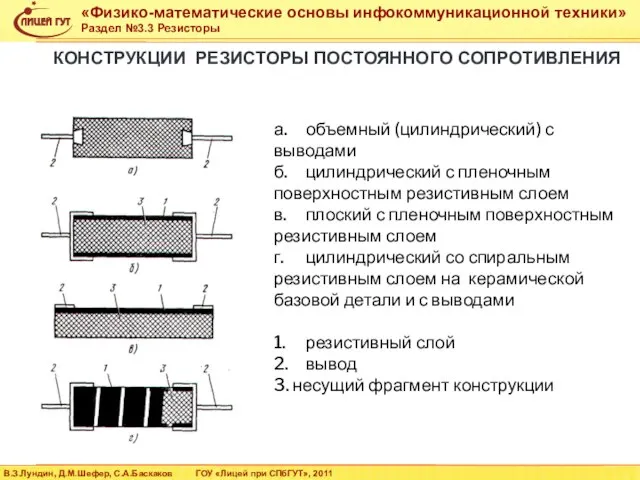
- 25. КОНСТРУКЦИИ РЕЗИСТОРЫ ПОСТОЯННОГО СОПРОТИВЛЕНИЯ а. объемный (цилиндрический) с выводами б. цилиндрический с пленочным поверхностным резистивным слоем
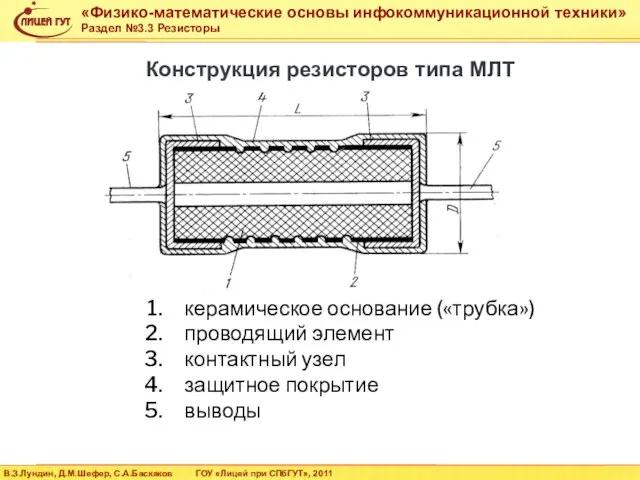
- 26. керамическое основание («трубка») проводящий элемент контактный узел защитное покрытие выводы Конструкция резисторов типа МЛТ
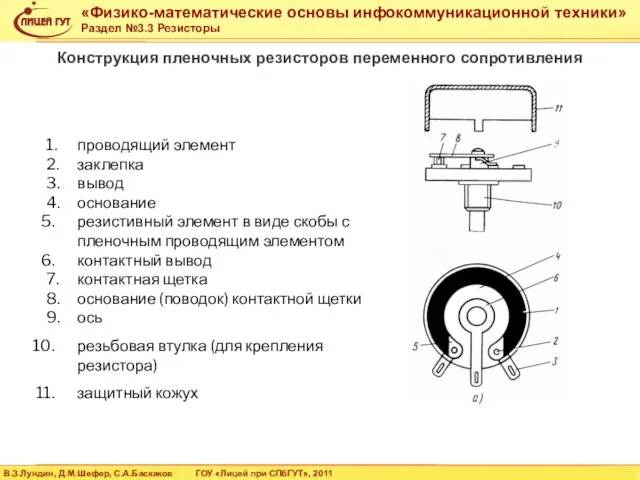
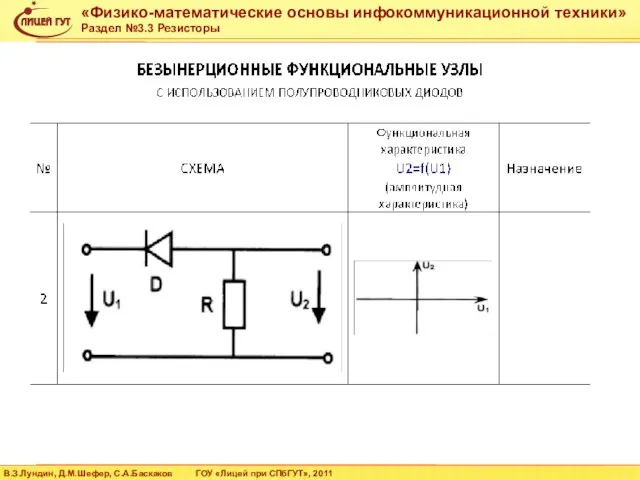
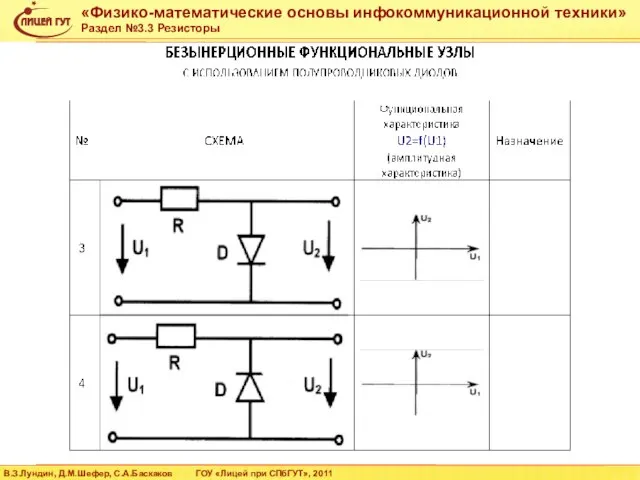
- 27. 1. проводящий элемент 2. заклепка 3. вывод 4. основание резистивный элемент в виде скобы с пленочным
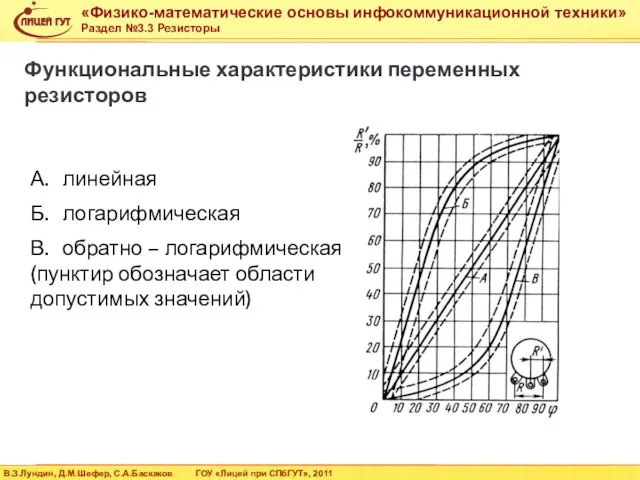
- 28. А. линейная Б. логарифмическая В. обратно – логарифмическая (пунктир обозначает области допустимых значений) Функциональные характеристики переменных
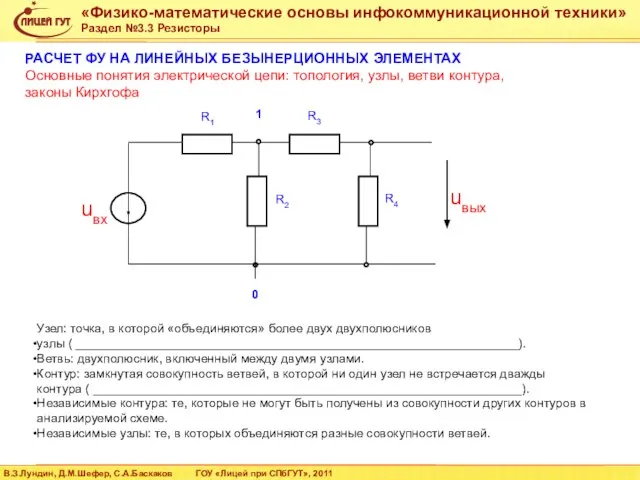
- 29. Узел: точка, в которой «объединяются» более двух двухполюсников узлы ( ________________________________________________________________). Ветвь: двухполюсник, включенный между двумя
- 30. Первый закон Кирхгофа: алгебраическая сумма токов в узле равна нулю. Второй закон Кирхгофа: алгебраическая сумма напряжений
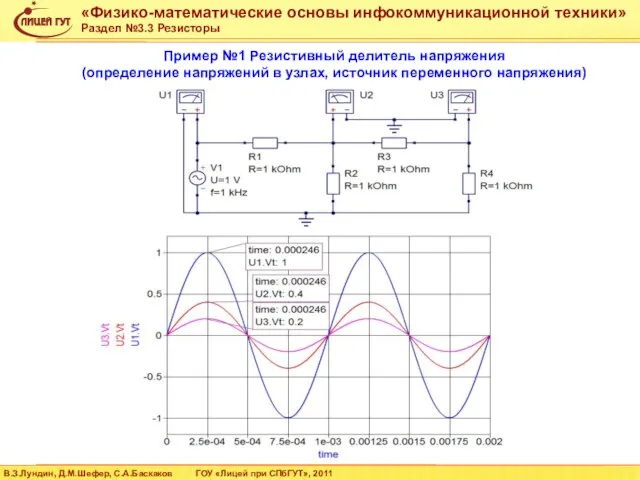
- 33. Пример №1 Резистивный делитель напряжения (определение токов в ветвях, источник постоянного напряжения)
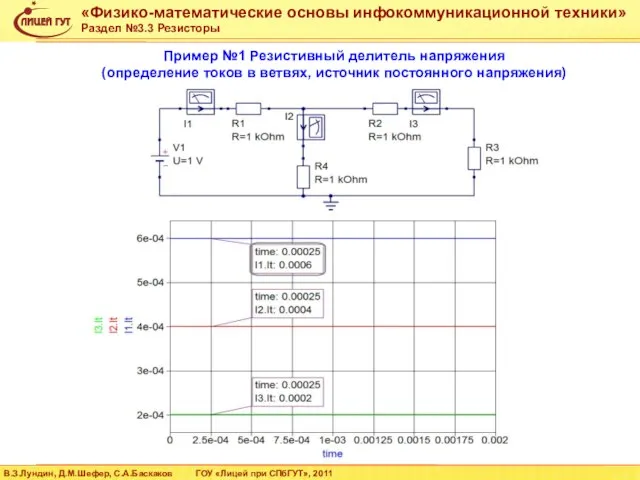
- 34. Пример №1 Резистивный делитель напряжения (определение напряжений в узлах, источник постоянного напряжения)
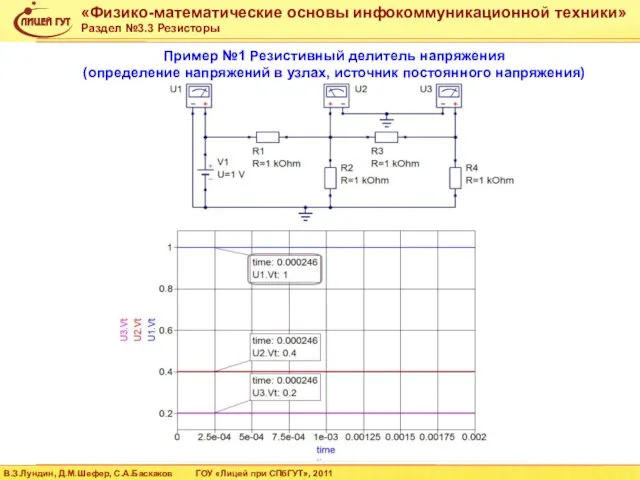
- 35. Пример №1 Резистивный делитель напряжения (определение токов в ветвях, источник переменного напряжения)
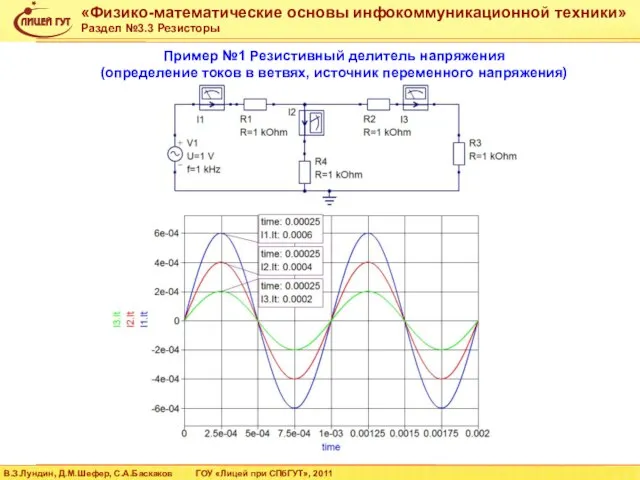
- 36. Пример №1 Резистивный делитель напряжения (определение напряжений в узлах, источник переменного напряжения)
- 37. A=[1000,1000,0;0,-1000,2000;1000,-1000,-1000] B=[-1;0;0] X=linsolve(A,B) X = 0.0006 0.0004 0.0002 Расчет в пакете SciLab Решение уравнения в матричной
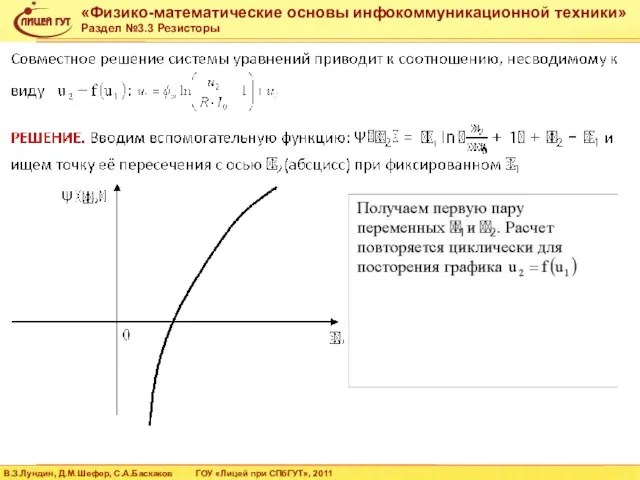
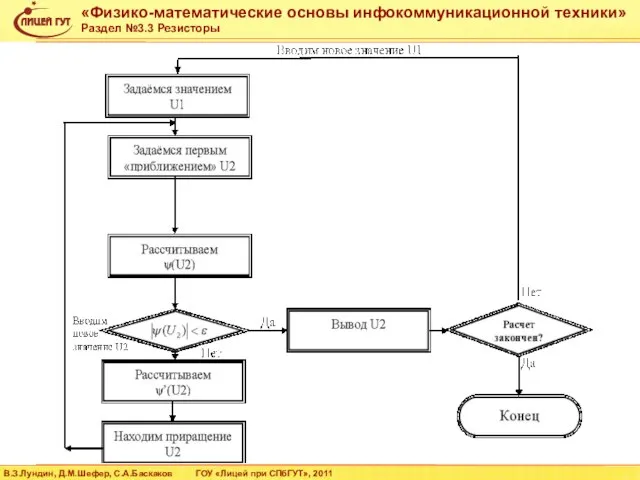
- 38. R=4000 U0=1 A=[R,R,0;0,-R,2*R;R,-R,-R] B=[-U0;0;0] I=linsolve(A,B) U(3)=I(3)*R U(2)=U(3)+I(2)*R U(1)=U(2)+I(1)*R Расчет в пакете SciLab Решение уравнения в матричной
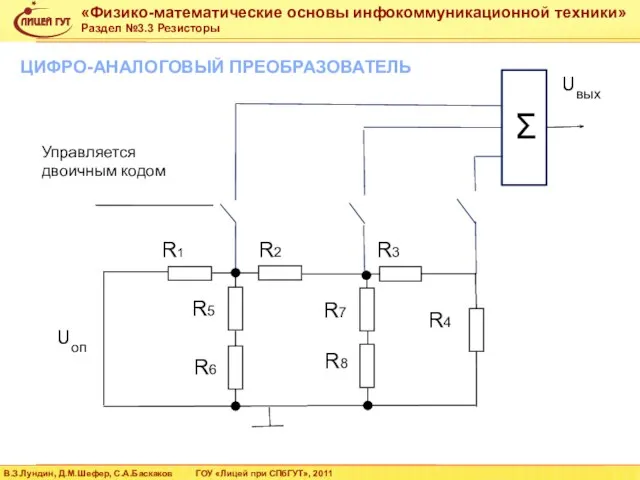
- 39. R4 Uоп R8 R6 R2 R1 R3 R5 R7 Σ Управляется двоичным кодом Uвых ЦИФРО-АНАЛОГОВЫЙ ПРЕОБРАЗОВАТЕЛЬ
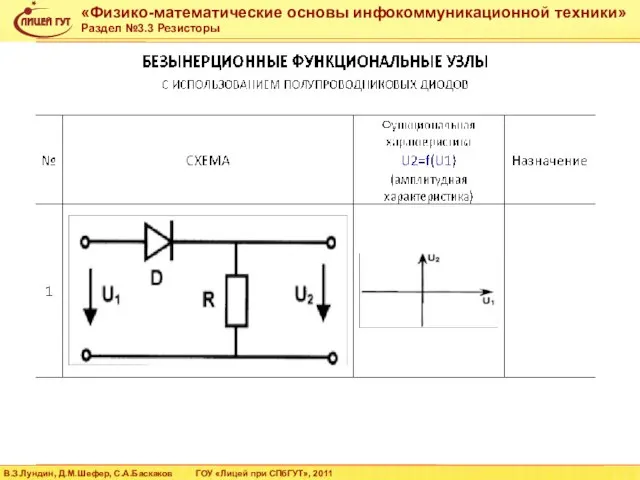
- 40. КОМПЛЕКСНАЯ РАБОТА №1 «ИССЛЕДОВАНИЕ БЕЗЫНЕРЦИОННЫХ ПАССИВНЫХ ФУНКЦИОНАЛЬНЫХ УЗЛОВ СРЕДСТВ СВЯЗИ». Задание Цель работы: исследование свойств резистивной
- 41. 3.Представляемые текстовые и графические материалы: 3.1 Пояснительная записка, оформленная с использованием текстового процессора OpenOffice. 3.2 Графический
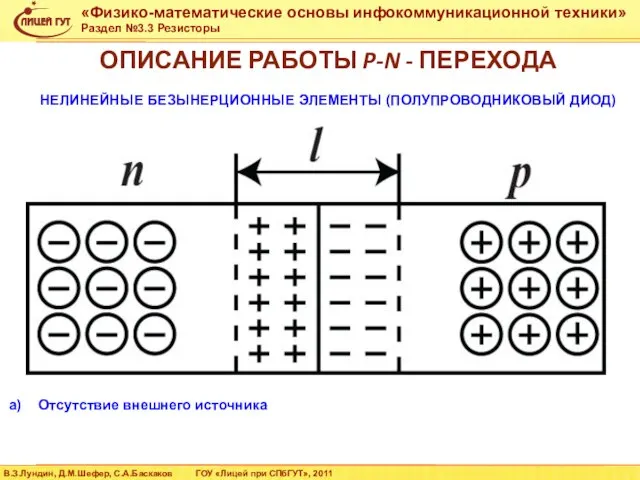
- 42. ОПИСАНИЕ РАБОТЫ P-N - ПЕРЕХОДА НЕЛИНЕЙНЫЕ БЕЗЫНЕРЦИОННЫЕ ЭЛЕМЕНТЫ (ПОЛУПРОВОДНИКОВЫЙ ДИОД) Отсутствие внешнего источника
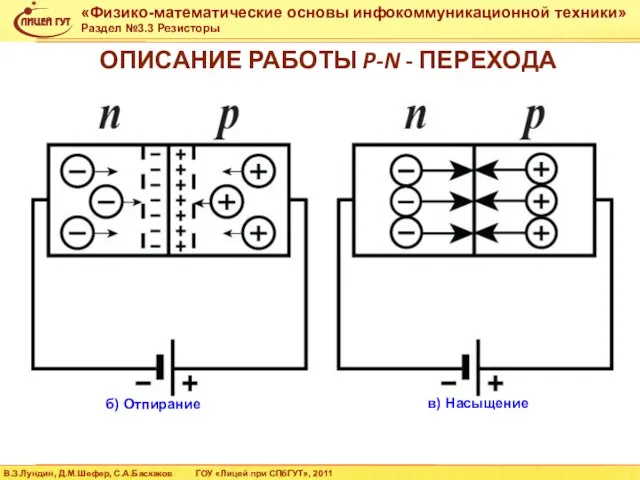
- 43. ОПИСАНИЕ РАБОТЫ P-N - ПЕРЕХОДА б) Отпирание в) Насыщение
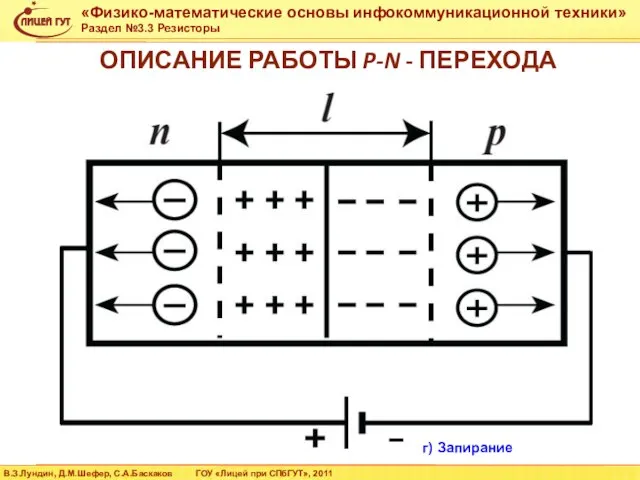
- 44. ОПИСАНИЕ РАБОТЫ P-N - ПЕРЕХОДА г) Запирание
- 45. МИКРОФОТОГРАФИИ ПОЛУПРОВОДНИКОВЫХ ИНТЕГРАЛЬНЫХ СХЕМ НА БИПОЛЯРНЫХ ТРАНЗИСТОРАХ (разное увеличение)
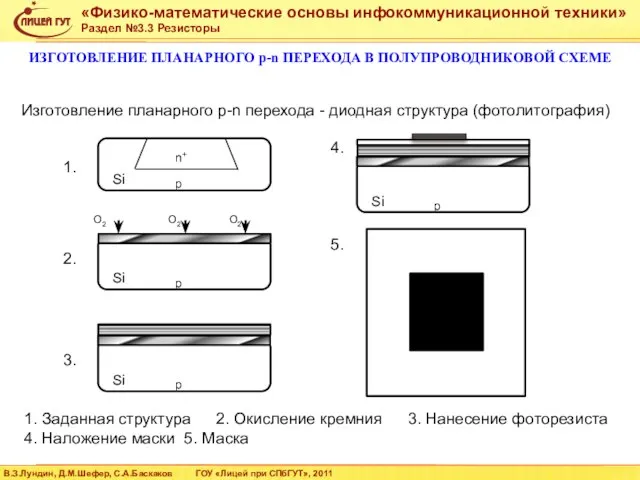
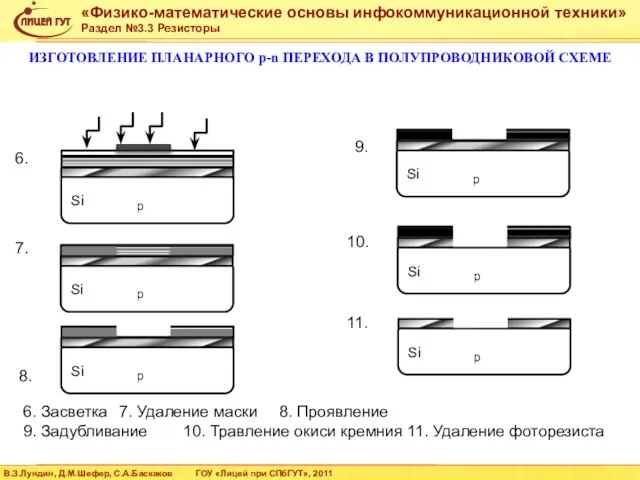
- 46. ИЗГОТОВЛЕНИЕ ПЛАНАРНОГО p-n ПЕРЕХОДА В ПОЛУПРОВОДНИКОВОЙ СХЕМЕ Изготовление планарного p-n перехода - диодная структура (фотолитография) 1.
- 47. Si-p О1 (первое окисление Si) Ф1 (первая фотолитография) Д1 (первая диффузия) Травление SiO2 Эпитаксия (слой n
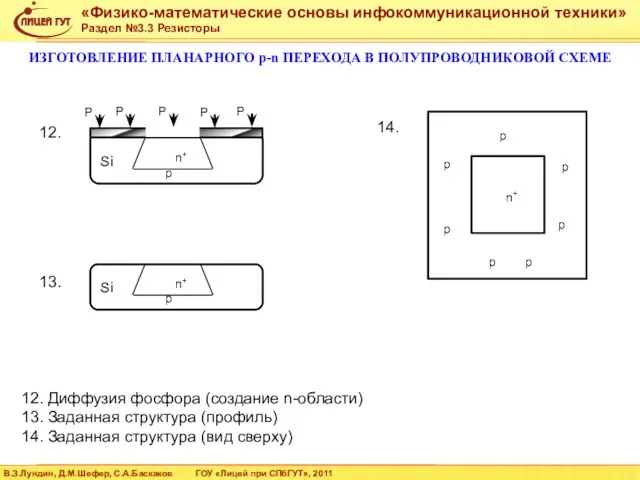
- 48. 12. Si p P P P P P n+ Si p n+ 13. 14. p p
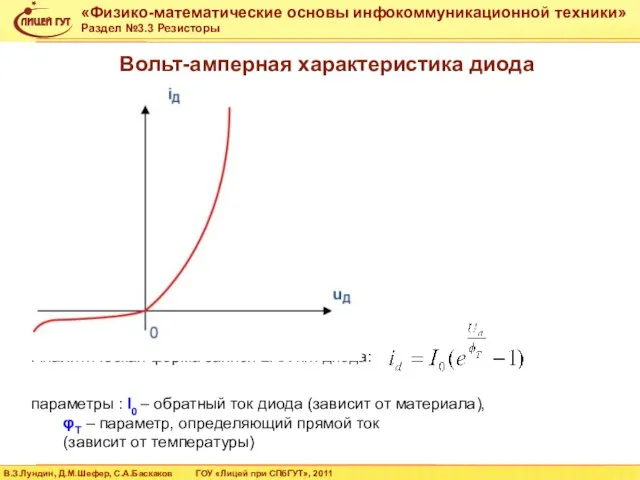
- 49. Вольт-амперная характеристика диода параметры : I0 – обратный ток диода (зависит от материала), φT – параметр,
- 51. Диоды. Вольт-амперная характеристика (ВАХ), аппроксимация ВАХ
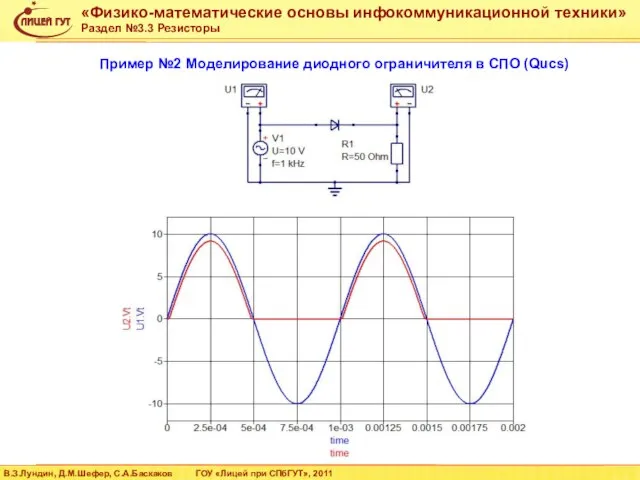
- 57. Пример №2 Моделирование диодного ограничителя в СПО (Qucs)
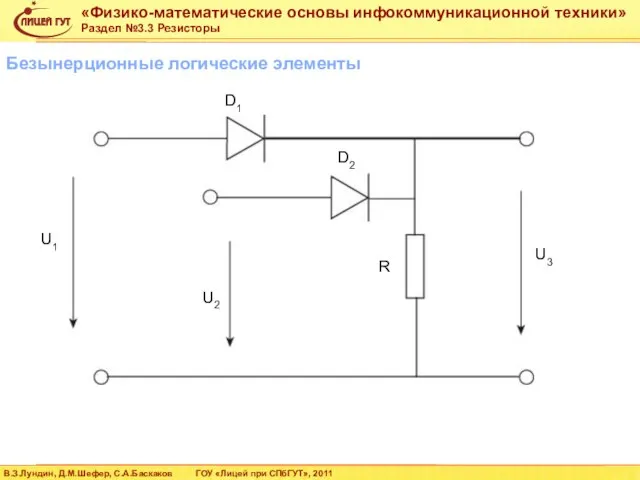
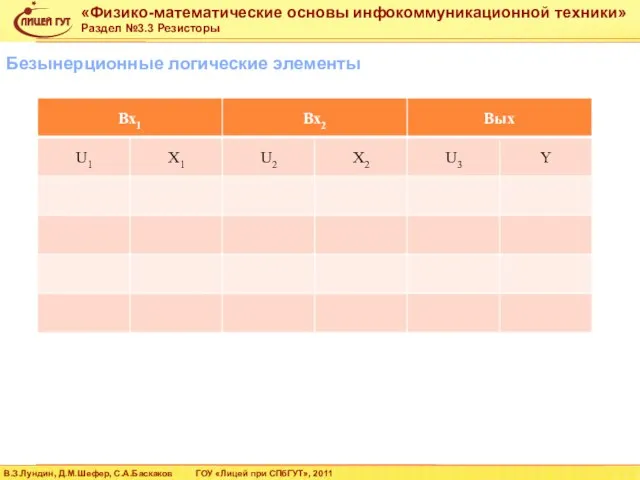
- 61. Безынерционные логические элементы D1 U1 U2 R D2 U3
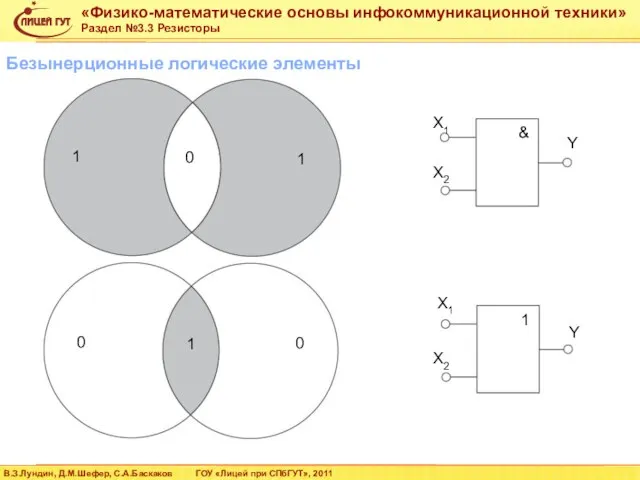
- 62. Безынерционные логические элементы
- 63. Безынерционные логические элементы X1 X1 X2 X2 Y Y & 1 0 1 1 0 0
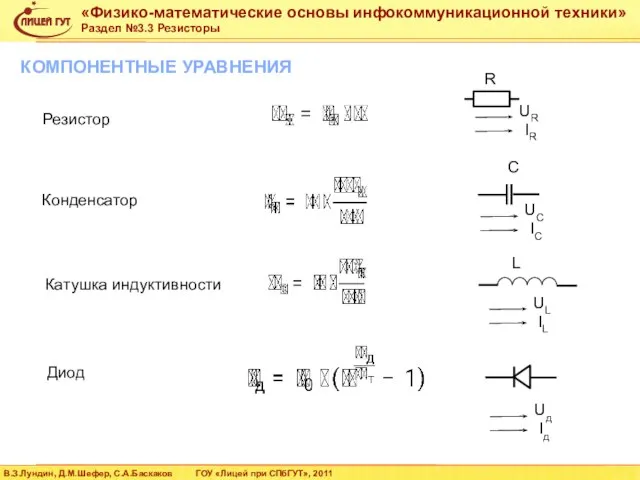
- 64. КОМПОНЕНТНЫЕ УРАВНЕНИЯ Резистор Конденсатор Катушка индуктивности Диод R C UR IR UC IC UL IL Uд
- 70. Скачать презентацию


















![A=[1000,1000,0;0,-1000,2000;1000,-1000,-1000] B=[-1;0;0] X=linsolve(A,B) X = 0.0006 0.0004 0.0002 Расчет в пакете SciLab](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/469301/slide-36.jpg)
![R=4000 U0=1 A=[R,R,0;0,-R,2*R;R,-R,-R] B=[-U0;0;0] I=linsolve(A,B) U(3)=I(3)*R U(2)=U(3)+I(2)*R U(1)=U(2)+I(1)*R Расчет в пакете SciLab](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/469301/slide-37.jpg)












 Презентация на тему Родник
Презентация на тему Родник Система ценообразования стримеров
Система ценообразования стримеров Сочинение по картине Ивана Ивановича Шишкина Корабельная роща
Сочинение по картине Ивана Ивановича Шишкина Корабельная роща Быт и культура коренных народов Севера. 9 класс
Быт и культура коренных народов Севера. 9 класс Наши добрые дела
Наши добрые дела Технические средства и инженерно-технические системы обеспечения транспортной безопасности
Технические средства и инженерно-технические системы обеспечения транспортной безопасности  Экономика возобновляемой энергетики и ветроэнергетики
Экономика возобновляемой энергетики и ветроэнергетики Кинетика нелинейных процессов
Кинетика нелинейных процессов Презентация на тему Материальные и экономические трудности
Презентация на тему Материальные и экономические трудности Презентация на тему Устройства ввода информации
Презентация на тему Устройства ввода информации  Anne Bronte
Anne Bronte Основы алгоритмизации и программирования
Основы алгоритмизации и программирования Информационно-практический проектна тему:«Соблюдение Правил дорожного движения пешеходами».
Информационно-практический проектна тему:«Соблюдение Правил дорожного движения пешеходами». ЗАВИСИМОСТЬ МЕЖДУ СИНУСОМ, КОСИНУСОМ И ТАНГЕНСОМ ОДНОГО И ТОГО ЖЕ УГЛА
ЗАВИСИМОСТЬ МЕЖДУ СИНУСОМ, КОСИНУСОМ И ТАНГЕНСОМ ОДНОГО И ТОГО ЖЕ УГЛА Учет и хранение фондов музея образовательной организации
Учет и хранение фондов музея образовательной организации Ернест Хамингуей
Ернест Хамингуей  SMM. Галкина Любовь
SMM. Галкина Любовь Эскиз
Эскиз Привлечение инвестиций
Привлечение инвестиций Методика анализа и оценки степени риска
Методика анализа и оценки степени риска AMPHIBIANS BULLFROG CROAK EGG FROG GILLS GUNGLE LEGS LEOPARD METAMORPHOSIS POND TADPOLE
AMPHIBIANS BULLFROG CROAK EGG FROG GILLS GUNGLE LEGS LEOPARD METAMORPHOSIS POND TADPOLE лекция 7 тема 1
лекция 7 тема 1 36f368566b7b47859a7e1559c9c90b96 (1)
36f368566b7b47859a7e1559c9c90b96 (1) Готовность ребёнка к школе
Готовность ребёнка к школе Презентация на тему Откуда взялся сфетофор
Презентация на тему Откуда взялся сфетофор Способы двигательной деятельности
Способы двигательной деятельности Сведения о морфемике и словообразовании
Сведения о морфемике и словообразовании В институтах Евросоюза официально равноправно используются 24 языка
В институтах Евросоюза официально равноправно используются 24 языка