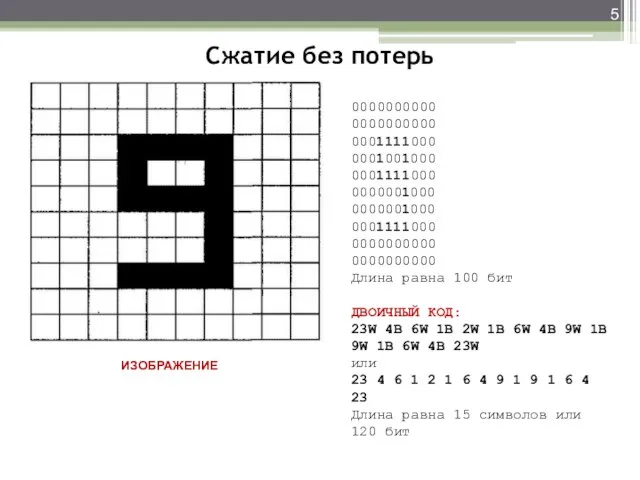
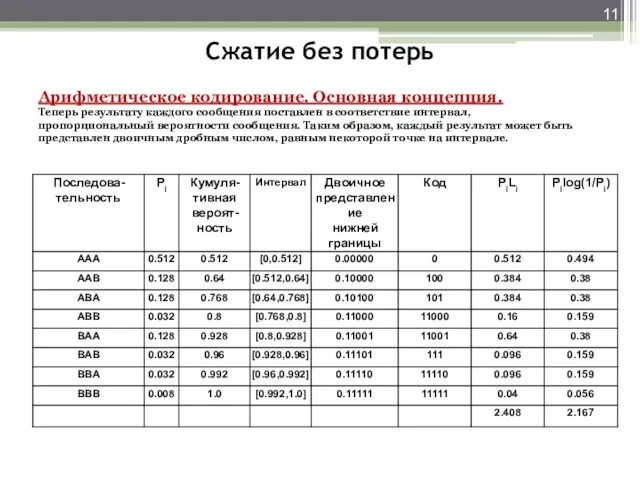
точек на дюйм): 3 740 000 бит (8.5’’ x 11’’ x 40 000 пелов на кв. дюйм)
ISDN (64 Кбит/с) – время передачи ~1 мин.
Два метода сжатия данных без потерь для факсимильной связи:
модифицированный код Хаффмана - группа 3.
модифицированный код READ (Relative Element Address Designate — относительное назначение адресов элементов) - группа 4.
Группа 3. Кодирование черных и белых значений с плотностью в 200 точек на дюйм (гориз.) и 100…200 (верт.). Предполагается, что передача сигнала осуществляется через модем по аналоговой телефонной линии. Передача данных ускоряется в три и более раз по сравнению с группой 2.
Группа 4. Черно-белый цифровой факсимильный стандарт. Эта группа предназначена для использования в цифровых сетях со скоростями до 64 Кбит/с. Стандартизированы разрешения от 200 до 400 точек на дюйм.Время передачи одной страницы сокращено до нескольких секунд по сравнению с несколькими минутами в предыдущих стандартах.










 Группа «Минимизация рисков перехода на ФГОС НОО. Мониторинг ФГОС НОО»
Группа «Минимизация рисков перехода на ФГОС НОО. Мониторинг ФГОС НОО» Everyday slang. Сленг на каждый день
Everyday slang. Сленг на каждый день Степень сравнения прилагательных
Степень сравнения прилагательных Открытки с 9 мая
Открытки с 9 мая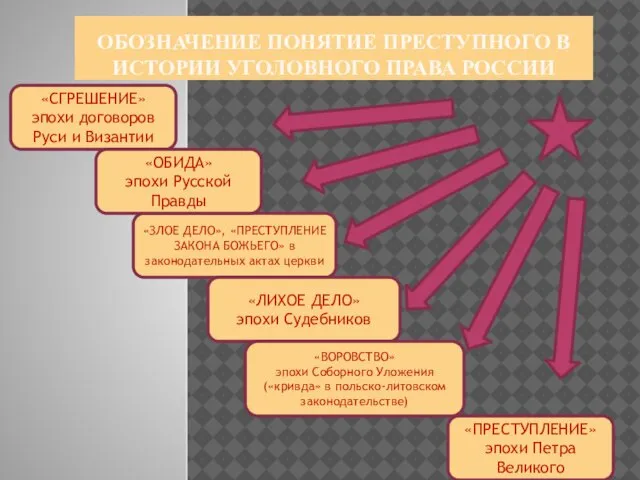 Понятие преступления и формы его множественности. Тема 3
Понятие преступления и формы его множественности. Тема 3 Разработка Учебных планов бакалавров и магистров по направлению «Энергетическое машиностроение» профиль подготовки бакалавров:
Разработка Учебных планов бакалавров и магистров по направлению «Энергетическое машиностроение» профиль подготовки бакалавров:  СТРУКТУРА РОССИЙСКОГО АВТОПАРКАГРУЗОВЫХ АВТОМОБИЛЕЙ ИАК «ВладВнешСервис», январь 2010
СТРУКТУРА РОССИЙСКОГО АВТОПАРКАГРУЗОВЫХ АВТОМОБИЛЕЙ ИАК «ВладВнешСервис», январь 2010 Прокачай в себе волонтера
Прокачай в себе волонтера praktika_po_zhkkh
praktika_po_zhkkh «Информационно-коммуникационные технологии в деятельности учителя математики»(18 часов)
«Информационно-коммуникационные технологии в деятельности учителя математики»(18 часов) Век медный,бронзовый, железный
Век медный,бронзовый, железный Литейное производство. Прибыли и холодильники отливок. (Лекция 7)
Литейное производство. Прибыли и холодильники отливок. (Лекция 7) Олимпида 2020
Олимпида 2020 Курительные смеси
Курительные смеси Holidays
Holidays Учимся мастерству
Учимся мастерству Муниципальное общеобразовательное учреждение«Средняя общеобразовательная школа № 13 »
Муниципальное общеобразовательное учреждение«Средняя общеобразовательная школа № 13 » Управление проектных продаж
Управление проектных продаж Арт-кластер Таврида
Арт-кластер Таврида Особенности предварительного расследования уголовных дел в отношении группы лиц с участием военнослужащих
Особенности предварительного расследования уголовных дел в отношении группы лиц с участием военнослужащих Рассмотрение дел о защите прав и законных интересов группы лиц. Лекция № 17
Рассмотрение дел о защите прав и законных интересов группы лиц. Лекция № 17 «Особенности преподавания русского языка по учебному комплексу Н.Г. Гольцовой, И.В. Шамшина»
«Особенности преподавания русского языка по учебному комплексу Н.Г. Гольцовой, И.В. Шамшина» Директор ФСИН России и его полномочия
Директор ФСИН России и его полномочия ЕВРАЗ: город друзей – город идей!
ЕВРАЗ: город друзей – город идей! НИ ДНЯ БЕЗ ПРАЗДНИКА!
НИ ДНЯ БЕЗ ПРАЗДНИКА! Презентация на тему Достопримечательности Бразилии
Презентация на тему Достопримечательности Бразилии  Как найти идею
Как найти идею Тургенев биография
Тургенев биография