Скоростной следящий электропривод. Синтез регулятора тока для настройки контура тока на оптимум по модулю

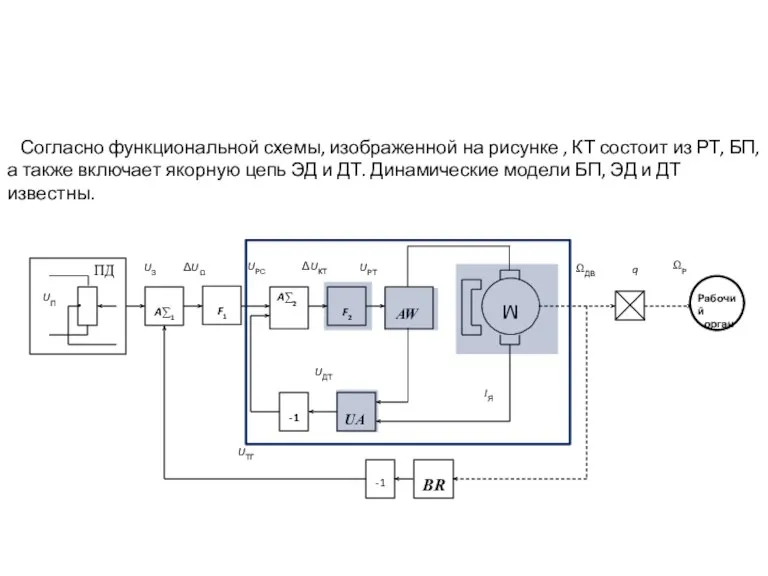
Согласно функциональной схемы, изображенной на рисунке , КТ состоит из РТ, БП, а также включает якорную цепь ЭД и ДТ. Динамические модели БП, ЭД и ДТ известны.

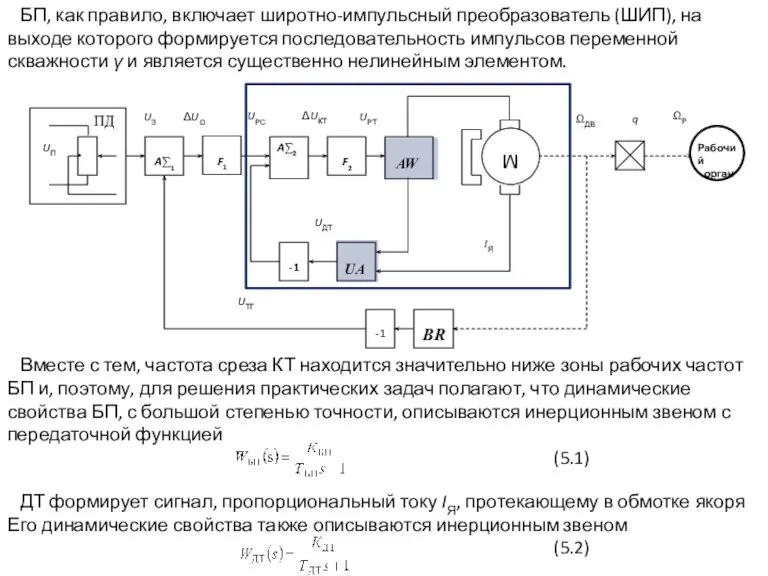
Вместе с тем, частота среза КТ находится значительно ниже зоны рабочих частот БП и, поэтому, для решения практических задач полагают, что динамические свойства БП, с большой степенью точности, описываются инерционным звеном с передаточной функцией
(5.1)
ДТ формирует сигнал, пропорциональный току IЯ, протекающему в обмотке якоря Его динамические свойства также описываются инерционным звеном
(5.2)
БП, как правило, включает широтно-импульсный преобразователь (ШИП), на выходе которого формируется последовательность импульсов переменной скважности γ и является существенно нелинейным элементом.

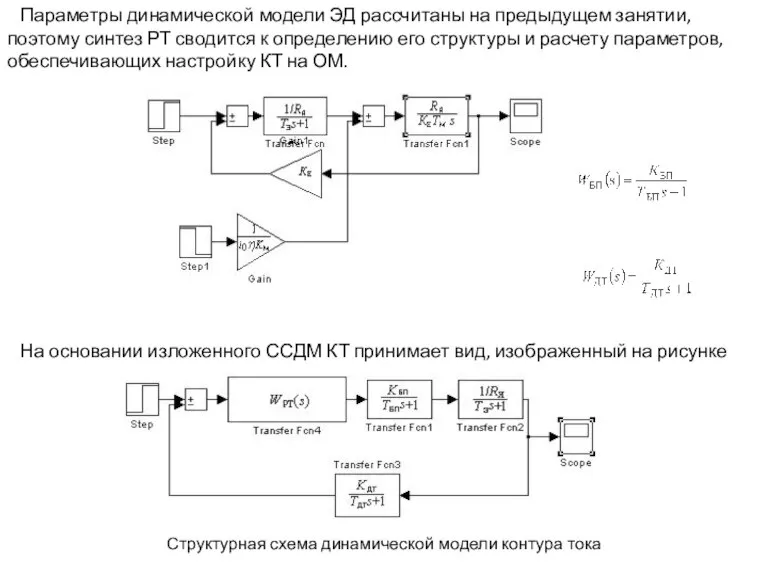
Параметры динамической модели ЭД рассчитаны на предыдущем занятии, поэтому синтез РТ сводится к определению его структуры и расчету параметров, обеспечивающих настройку КТ на ОМ.
На основании изложенного ССДМ КТ принимает вид, изображенный на рисунке
Структурная схема динамической модели контура тока

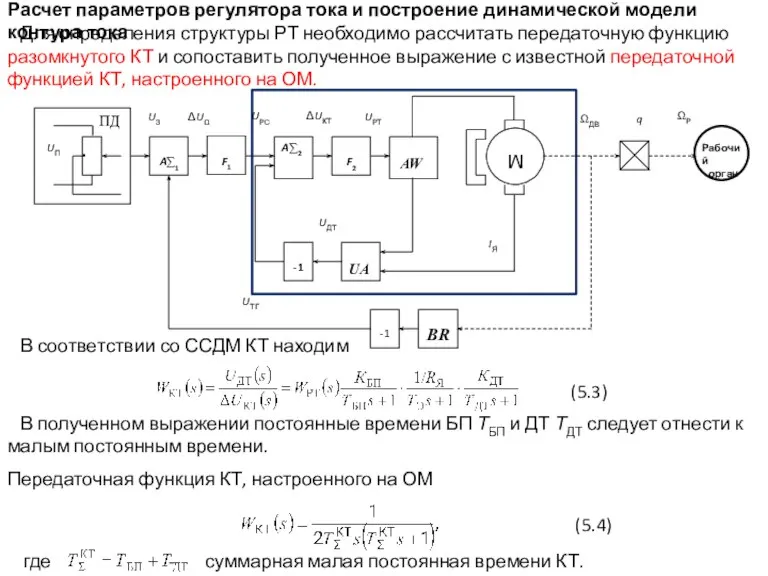
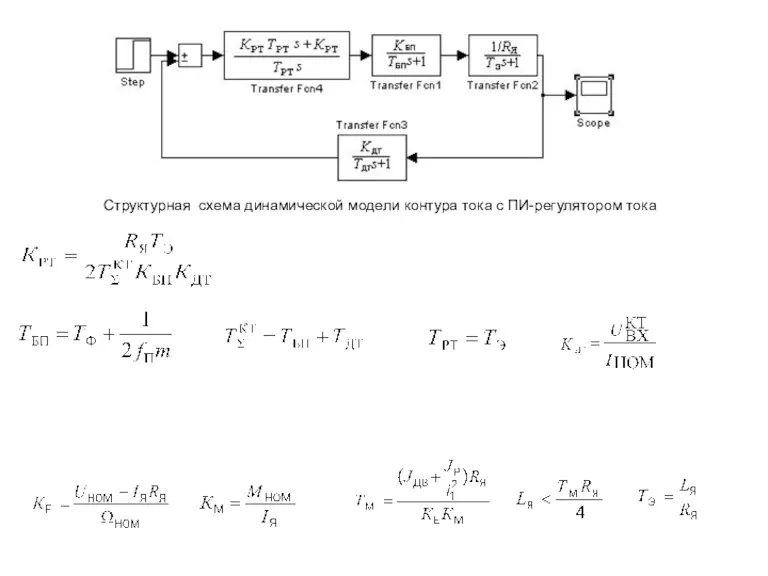
где - суммарная малая постоянная времени КТ.
Расчет параметров регулятора тока и построение динамической модели контура тока
Для определения структуры РТ необходимо рассчитать передаточную функцию разомкнутого КТ и сопоставить полученное выражение с известной передаточной функцией КТ, настроенного на ОМ.
В соответствии со ССДМ КТ находим
(5.3)
В полученном выражении постоянные времени БП ТБП и ДТ ТДТ следует отнести к малым постоянным времени.
Передаточная функция КТ, настроенного на ОМ
(5.4)

(5.5)
Полученное выражение по своей структуре является передаточной функцией ПИ-регулятора
(5.6)
Сравнив (5.5) и (5.6), получим формулы для расчета коэффициента передачи КРТ и постоянной времени ТРТ РТ
(5.7)
(5.8)
Для вычисления коэффициента передачи датчика тока необходимо применить формулу
(5.9)
Приравнивая правые части выражений (5.3) и (5.4)
находим передаточную функцию РТ

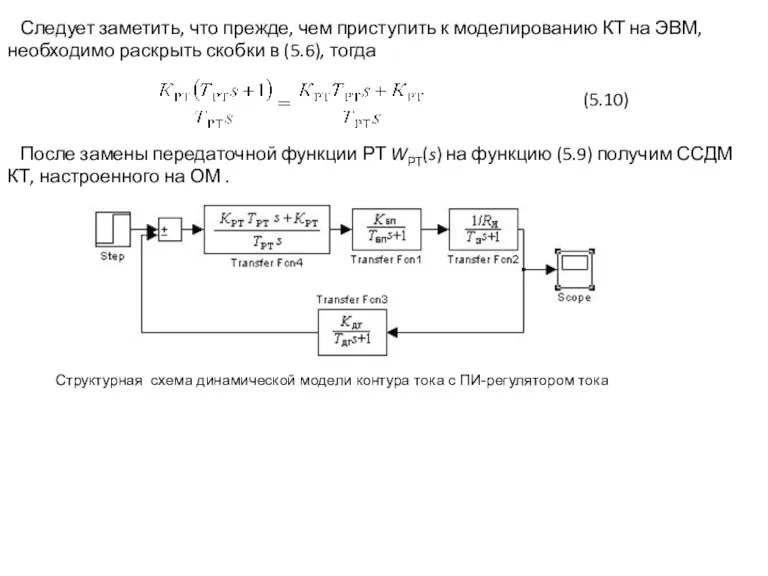
Следует заметить, что прежде, чем приступить к моделированию КТ на ЭВМ, необходимо раскрыть скобки в (5.6), тогда
(5.10)
После замены передаточной функции РТ WРТ(s) на функцию (5.9) получим ССДМ КТ, настроенного на ОМ .
Структурная схема динамической модели контура тока с ПИ-регулятором тока

Пример Определить параметры РТ и построить динамическую модель КТ скоростного следящего ЭП с ЭД МИ-22, если коэффициент передачи БП КБП=30; постоянная времени фильтра ТФ=0,0024 с; число пульсаций выпрямленного напряжения за период m=2; частота питающего напряжения бортового преобразователя fП=400 Гц; входное напряжение суммирующего усилителя контура тока U = 10 В, постоянная времени ДТ ТДТ=0,001 с.
1. Рассчитываем коэффициент передачи ДТ по формуле (5.9)
При использовании в качестве датчика тока шунта, его сопротивление определяется по формуле
2. Рассчитываем суммарную малую постоянную времени КТ.
Номинальная мощность ЭД МИ-22 РНОМ=0,37 кВт. Согласно методических указаний номинальная мощность выбранного ЭД превышает значение 0,2 кВт. Поэтому постоянная времени БП определится по формуле
Решение.

Для расчета суммарной малой постоянной времени КТ воспользуемся выражением (5.4), тогда
3. Определяем параметры РТ.
По формуле (5.7) рассчитываем коэффициент передачи РТ
Постоянная времени РТ, согласно (5.8), определится в виде:
4. Для построения ССДМ КТ в соответствии с (5.10), находим
Подставив заданные и рассчитанные числовые значения в схему ССДМ КТ, получаем ССДМ КТ, настроенного на ОМ с числовыми значениями.

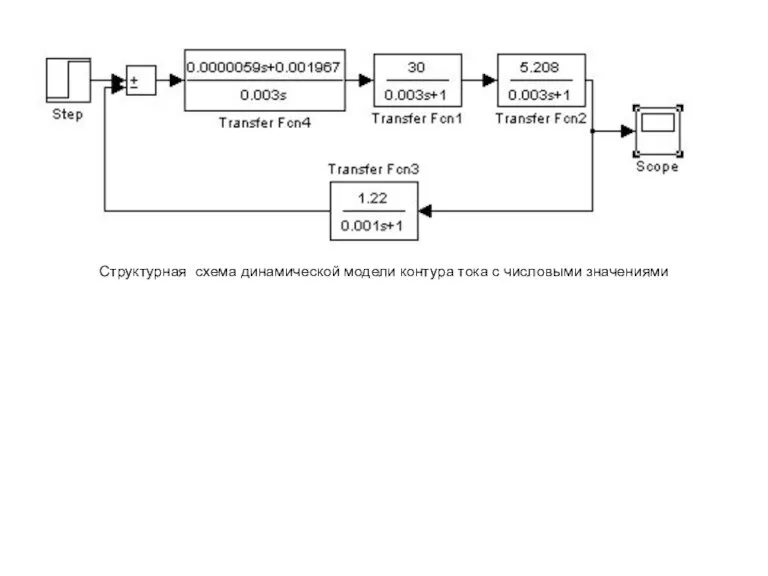
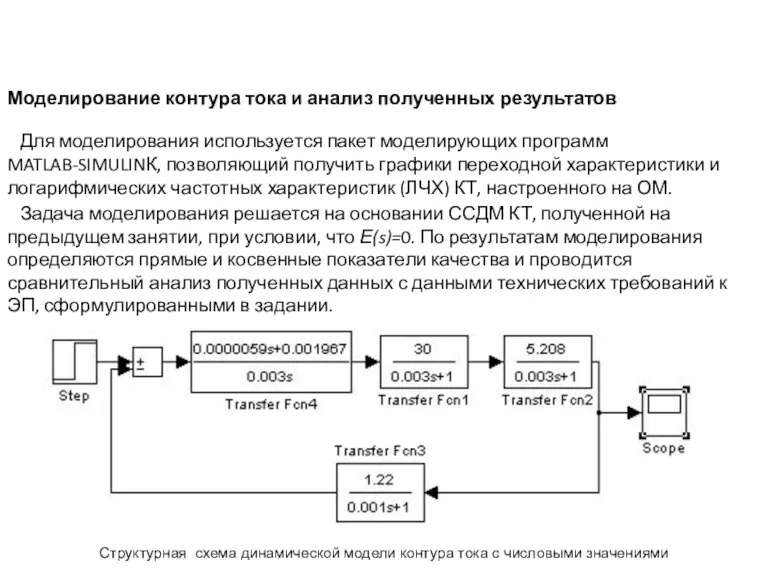
Структурная схема динамической модели контура тока с числовыми значениями

Структурная схема динамической модели контура тока с ПИ-регулятором тока

Моделирование контура тока и анализ полученных результатов
Для моделирования используется пакет моделирующих программ MATLAB-SIMULINК, позволяющий получить графики переходной характеристики и логарифмических частотных характеристик (ЛЧХ) КТ, настроенного на ОМ.
Задача моделирования решается на основании ССДМ КТ, полученной на предыдущем занятии, при условии, что Е(s)=0. По результатам моделирования определяются прямые и косвенные показатели качества и проводится сравнительный анализ полученных данных с данными технических требований к ЭП, сформулированными в задании.
Структурная схема динамической модели контура тока с числовыми значениями

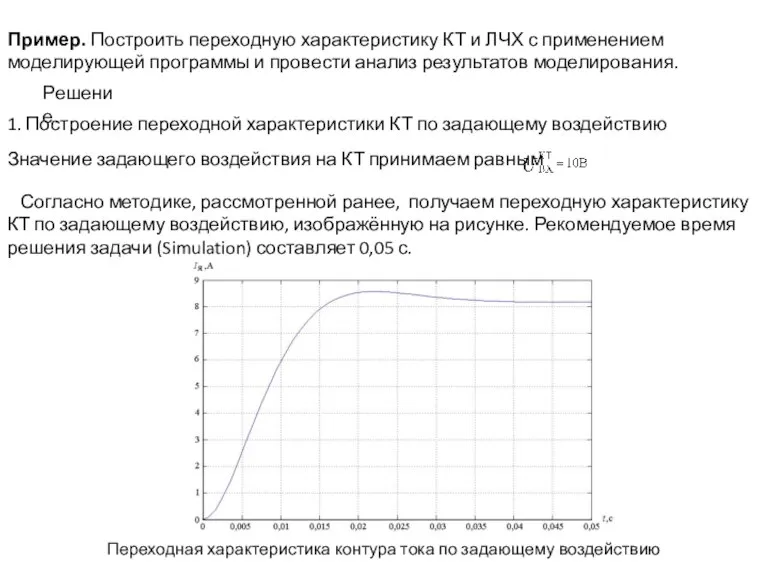
Пример. Построить переходную характеристику КТ и ЛЧХ с применением моделирующей программы и провести анализ результатов моделирования.
Решение.
1. Построение переходной характеристики КТ по задающему воздействию
Значение задающего воздействия на КТ принимаем равным
Согласно методике, рассмотренной ранее, получаем переходную характеристику КТ по задающему воздействию, изображённую на рисунке. Рекомендуемое время решения задачи (Simulation) составляет 0,05 с.
Переходная характеристика контура тока по задающему воздействию

2. Построение ЛЧХ КТ
Для построения ЛЧХ необходимо определить передаточную функцию разомкнутого контура тока, которая определяется как отношение изображения по Лапласу тока якоря IЯ(s) к сигналу рассогласования с выхода суммирующего усилителя КТ
(5.11)
Поскольку все элементы в цепи КТ соединены последовательно, то выражение (5.11) определится как произведение всех передаточных функций элементов, входящих в КТ
(5.12)
В выражении (5.12) является передаточной функцией обмотки якоря.
Таким образом, в командном окне (Command Windows) программы Matlab 6.5 необходимо составить произведение (5.12), предварительно обозначив соответствующие передаточные функции как:
sys1=
sys2=
sys3=
sys4=
.

Для набора обозначенных передаточных функций необходимо предварительно записать числитель и знаменатель соответствующего блока. Например, если передаточная функция имеет вид
то в командном окне необходимо произвести следующую запись
num1=[b1 b0];
den1=[d1 d0];
sys1=tf(num1,den1).
После набора программы для контроля правильности обозначений следует нажать Enter. Коэффициенты числителя b1, b0 и знаменателя d1, d0 записываются через пробел.
Для построения ЛЧХ КТ используется результат произведения (5.12). Чтобы построить ЛЧХ, необходимо задать логарифмическое пространство logspace(-n,n). Значение (-n,n) обозначает показатели степени при основании 10, указывающие диапазон частот, в котором будут построены ЛЧХ. Например, если n=3, диапазон частот составляет
10-3 – 103 рад/с, т.е. 0,001 – 1000 рад/с.

Соответственно программа для получения ЛЧХ КТ принимает вид:
>> num1=[0.0000059 0.001967];
>> den1=[0.003 0];
>> sys1=tf(num1,den1)
Transfer function:
5.9e-006 s + 0.001967
---------------------
0.003 s
>> num2=[30];
>> den2=[0.003 1];
>> sys2=tf(num2,den2)
Transfer function:
30
-----------
0.003 s + 1
>> num3=[5.208];
>> den3=[0.003 1];
>> sys3=tf(num3,den3)
Transfer function:
5.208
-----------
0.003 s + 1
>> num4=[1.22];
>> den4=[0.001 1];
>> sys4=tf(num4,den4)
Transfer function:
1.22
-----------
0.001 s + 1
>> sys5=sys1*sys2*sys3*sys4
Transfer function:
0.001125 s + 0.3749
----------------------------------------------------
2.7e-011 s^4 + 4.5e-008 s^3 + 2.1e-005 s^2 + 0.003 s
>> w=logspace(-3,3);
>> bode(sys5,w)
На следующем рисунке представлены результаты моделирования.

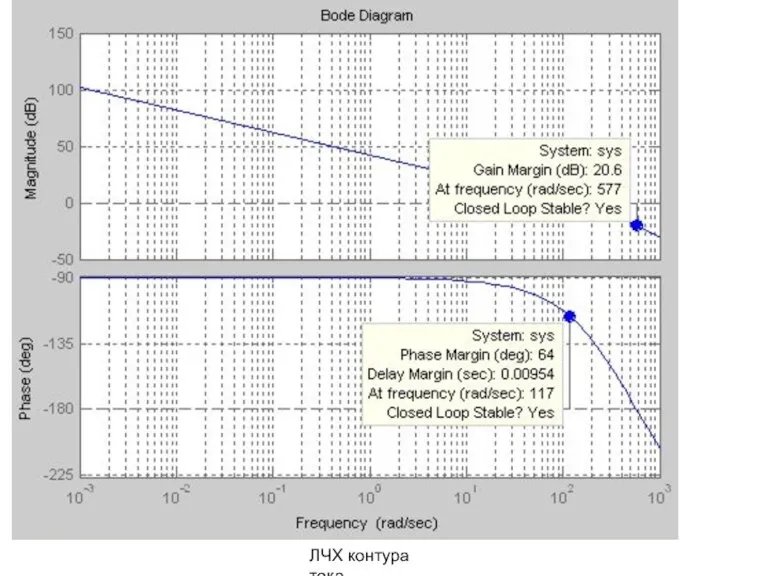
ЛЧХ контура тока

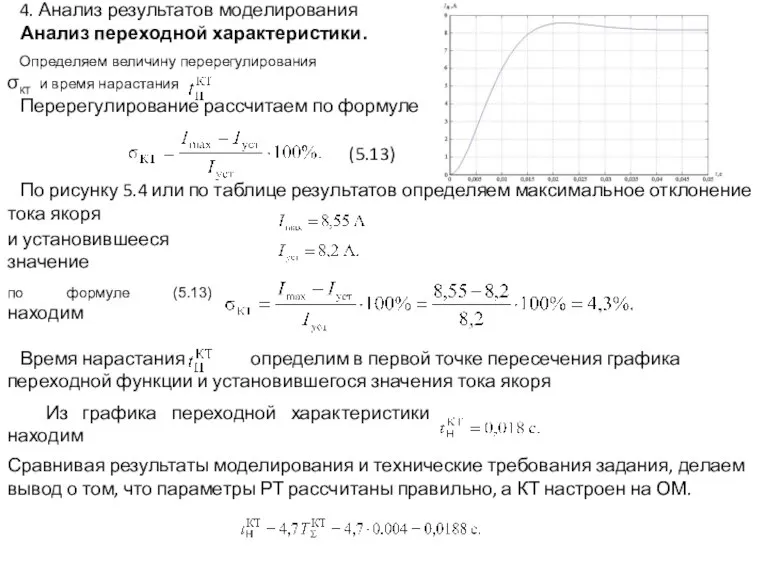
Перерегулирование рассчитаем по формуле
Определяем величину перерегулирования σКТ и время нарастания
Время нарастания определим в первой точке пересечения графика переходной функции и установившегося значения тока якоря
4. Анализ результатов моделирования
Анализ переходной характеристики.
.
(5.13)
По рисунку 5.4 или по таблице результатов определяем максимальное отклонение тока якоря
и установившееся значение
по формуле (5.13) находим
.
Из графика переходной характеристики находим
Сравнивая результаты моделирования и технические требования задания, делаем вывод о том, что параметры РТ рассчитаны правильно, а КТ настроен на ОМ.

Частота соответствует точке пересечения логарифмической фазо-частотной характеристики (Phase) с линией -180° (-π).
Анализ ЛЧХ.
Запас устойчивости по фазе находим по нижнему графику (Phase) на частоте среза
Значение запаса по фазе (deg)
Напомним, что частота среза соответствует точке пересечения логарифмической амплитудно-частотной характеристики (Magnitude) с осью частот.
Для проверки необходимо рассчитать частоту среза аналитически
Полученное значение соответствует результатам моделирования.
Запас устойчивости по амплитуде определяем по верхнему графику (Magnitude)
Значение запаса по амплитуде
Запасы устойчивости по фазе и амплитуде соответствуют настроенным параметрам ПИ-регулятора и удовлетворяют требованиям технического задания

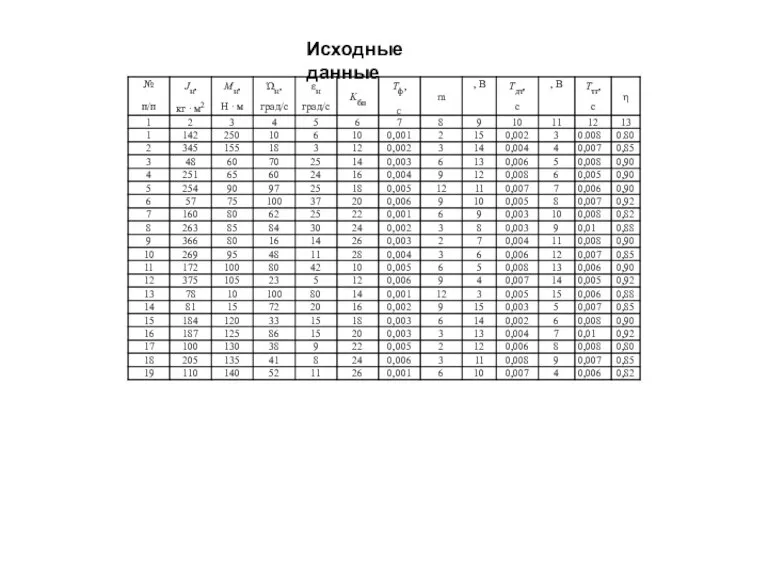
Исходные данные