Содержание
- 2. Перемещение из одной точки в другую может быть различным Школа Левый берег Тверцы Дом
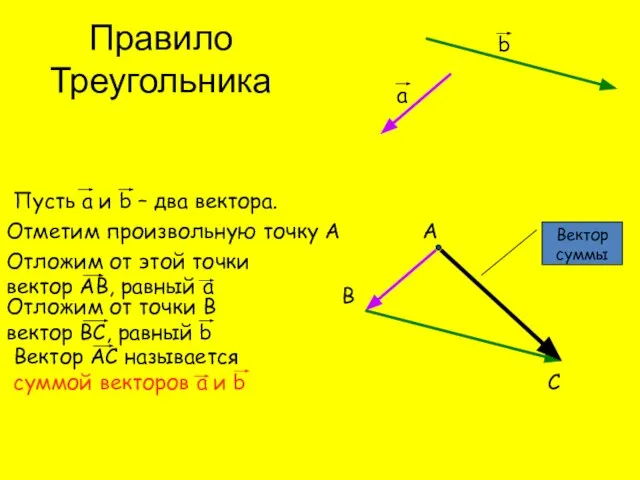
- 3. Пусть а и b – два вектора. а b Отметим произвольную точку А А Отложим от
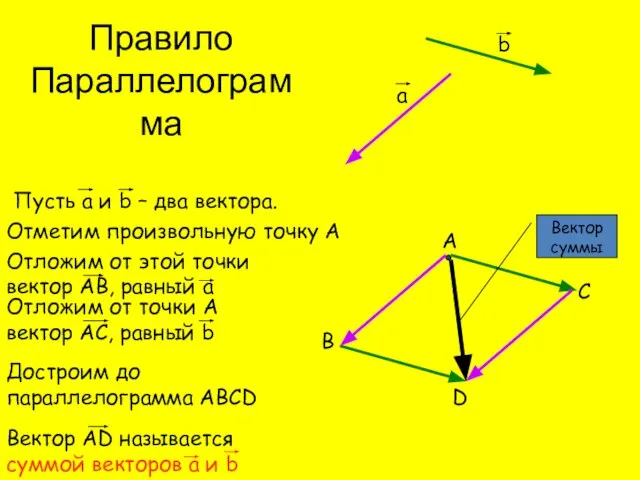
- 4. Пусть а и b – два вектора. а b Отметим произвольную точку А А Отложим от
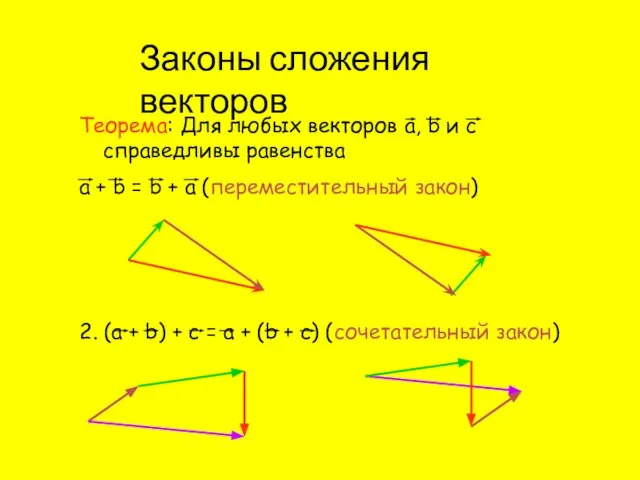
- 5. Законы сложения векторов Теорема: Для любых векторов а, b и с справедливы равенства а + b
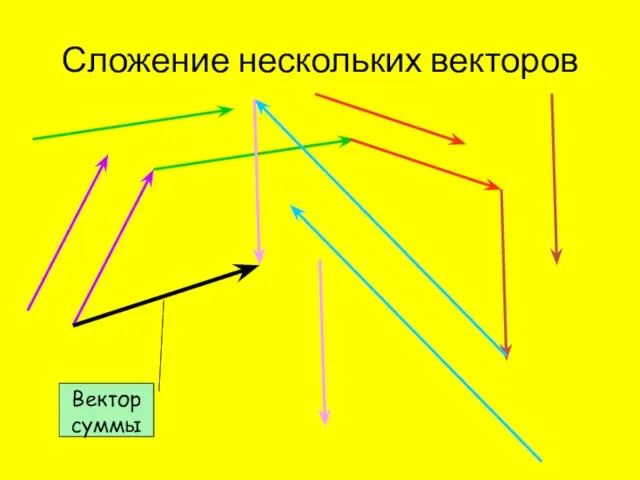
- 6. Сложение нескольких векторов Вектор суммы
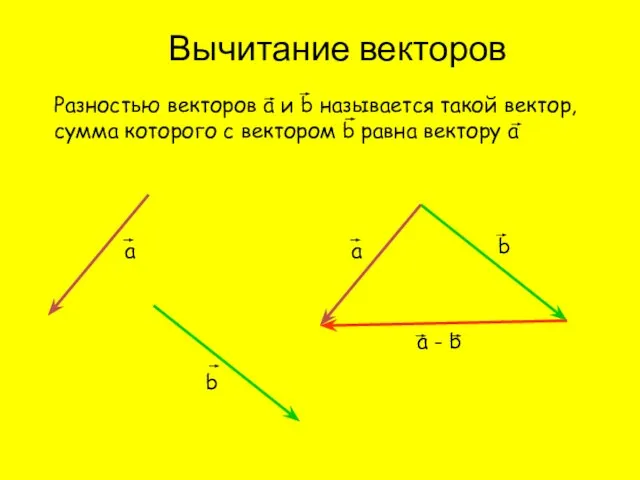
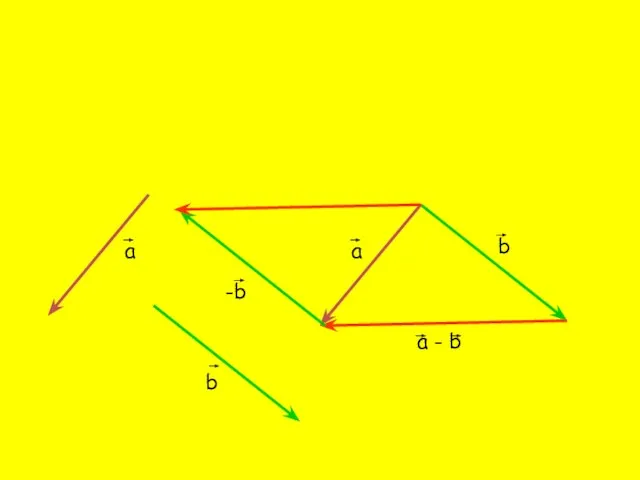
- 7. Вычитание векторов Разностью векторов а и b называется такой вектор, сумма которого с вектором b равна
- 8. Тест Вопрос №1 Верно ли, что сумма длин двух неколлинеарных векторов равна длине их суммы? да
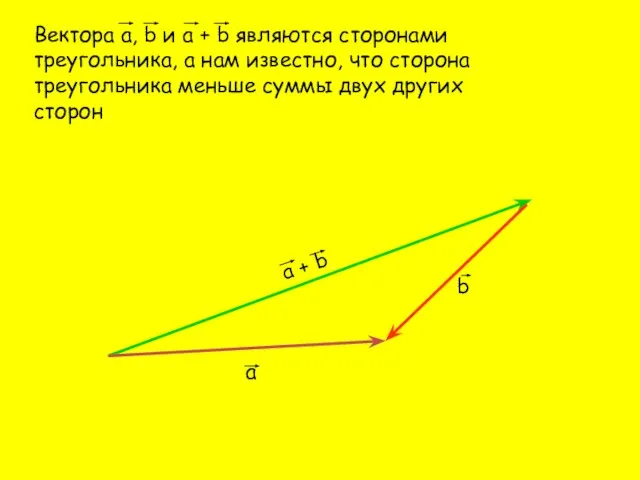
- 9. Вектора а, b и а + b являются сторонами треугольника, а нам известно, что сторона треугольника
- 10. Вопрос №2 Может ли сумма нескольких векторов равняться нулевому вектору? да нет
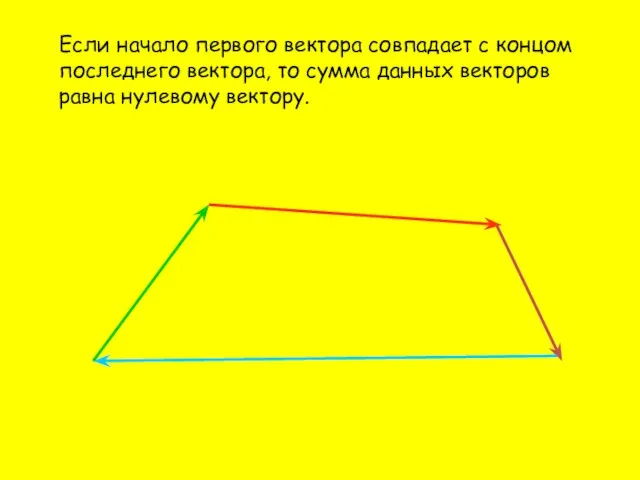
- 11. Если начало первого вектора совпадает с концом последнего вектора, то сумма данных векторов равна нулевому вектору.
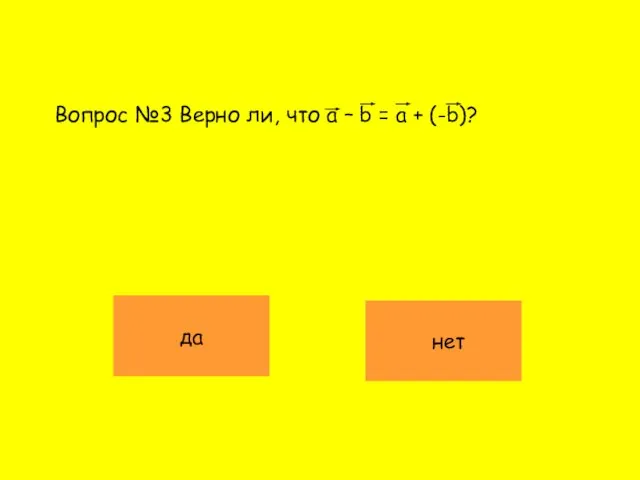
- 12. Вопрос №3 Верно ли, что a – b = a + (-b)? да нет
- 13. а b а b а - b -b
- 15. Скачать презентацию


 УАТТ ДЖЕЙМС (1736–1819)
УАТТ ДЖЕЙМС (1736–1819) Физика 7
Физика 7 Разработка проектной идеи образовательного ресурса. №3
Разработка проектной идеи образовательного ресурса. №3 Хумус Бар
Хумус Бар Лекция 7
Лекция 7 Презентация на тему Гаршин сказка о жабе и розе
Презентация на тему Гаршин сказка о жабе и розе  Презентация на тему Белки
Презентация на тему Белки Презентация на тему Применение жиров
Презентация на тему Применение жиров  Первомайская центральная районная детская библиотека
Первомайская центральная районная детская библиотека Чудо Земли - хлеб
Чудо Земли - хлеб Бытовой жанр в русской живописи конца ХVIII в. - первой половины ХIХ в
Бытовой жанр в русской живописи конца ХVIII в. - первой половины ХIХ в Выставка работ
Выставка работ Отчет о проделанной работе с резидентами по дисциплине Клиническая фармакология, 2019-2021 годы обучения
Отчет о проделанной работе с резидентами по дисциплине Клиническая фармакология, 2019-2021 годы обучения 孔子学院在乌克兰和俄罗斯
孔子学院在乌克兰和俄罗斯 Презентация на тему Саудовская Аравия
Презентация на тему Саудовская Аравия  Методические рекомендации к заполнению классного журнала в государственном образовательном учреждении общего образования
Методические рекомендации к заполнению классного журнала в государственном образовательном учреждении общего образования Представление нечисловой информации
Представление нечисловой информации Дед Мороз на новогодних открытках
Дед Мороз на новогодних открытках Разветвляющийся алгоритм
Разветвляющийся алгоритм Пролог к изучению поэмы Н.В. Гоголя «Мертвые души»
Пролог к изучению поэмы Н.В. Гоголя «Мертвые души» Познавательные процессы (память)
Познавательные процессы (память) Диспансеризация сельскохозяйственных животных при внутренних болезнях
Диспансеризация сельскохозяйственных животных при внутренних болезнях Инвестиционная деятельность предприятия
Инвестиционная деятельность предприятия «МОЯ СТРАНА – МОЯ РОССИЯ»
«МОЯ СТРАНА – МОЯ РОССИЯ» Любовная лирика Ф.И.Тютчева
Любовная лирика Ф.И.Тютчева Нестероидные противовоспалительные средства
Нестероидные противовоспалительные средства Почему болеют мои одноклассники
Почему болеют мои одноклассники Штат Колорадо
Штат Колорадо