Слайд 21. Определения
Ненулевой вектор х называется собственным вектором матрицы А, если найдется такое

число , что
Число называется собственным (характеристическим) значением (числом) матрицы А, соответствующим вектору х.
далее
Слайд 3
Характеристическим уравнением матрицы А называется уравнение:
Пример 1.
назад

Слайд 4Пример 1. Составить характеристические уравнения для матриц
Решение:

Слайд 5Решение (Пример 1):
Составим характеристическое уравнение для матрицы А:
далее

Слайд 6Решение (Пример 1):
Составим характеристическое уравнение для матрицы В:
назад

Слайд 72. Нахождение собственных значений матрицы
Для нахождения собственных значений матрицы А необходимо решить

характеристическое уравнение
Пример 2.
назад
Слайд 8Пример 2. Найти собственные значения матриц
Решение:

Слайд 9Решение (Пример 2):
Решим характеристическое уравнение матрицы А:
далее

Слайд 10Решение (Пример 2):
Решим характеристическое уравнение матрицы В:
назад

Слайд 113. Нахождение собственных векторов матрицы
Для нахождения собственных векторов матрицы А необходимо решить

систему линейных однородных уравнений
Пример 3.
назад
Слайд 12Пример 3. Найти собственные векторы следующих матриц
Решение:

Слайд 13Решение (Пример 3) для матрицы А:
1) Решив характеристическое уравнение для матрицы

А, получили
2) Для собственного значения составим систему линейный однородных уравнений:
далее
Слайд 14Решение (Пример 3) для матрицы А:
3) Для собственного значения составим систему

линейный однородных уравнений:
далее
Слайд 15Решение (Пример 3) для матрицы В:
1) Решив характеристическое уравнение для матрицы

В, получили
2) Для собственного значения составим систему линейный однородных уравнений:
далее
Слайд 16Решение (Пример 3) для матрицы В:
3) Для собственного значения составим систему

линейный однородных уравнений:
далее
Слайд 17Решение (Пример 3) для матрицы В:
4) Для собственного значения составим систему

линейный однородных уравнений:
назад
















 Speaking about the weather
Speaking about the weather Что изучает физика?
Что изучает физика? Мифы о журналистике. То, что вы хотели знать, но боялись спросить
Мифы о журналистике. То, что вы хотели знать, но боялись спросить Строительно-монтажные работы при восстановлении объектов ж/д транспорта при возникновении ЧС
Строительно-монтажные работы при восстановлении объектов ж/д транспорта при возникновении ЧС Ремонт ленточного накопителя IBM 3590
Ремонт ленточного накопителя IBM 3590 Деление дробей
Деление дробей Развитие творческой деятельности школьников в рамках работы лаборатории ранней профессиональной ориентации
Развитие творческой деятельности школьников в рамках работы лаборатории ранней профессиональной ориентации Цветотип
Цветотип Формирование ключевых компетенций на уроках географии
Формирование ключевых компетенций на уроках географии Презентация на тему С огнем не играй - пожар не затевай!
Презентация на тему С огнем не играй - пожар не затевай! Наши любимые сказки Андерсена
Наши любимые сказки Андерсена Soonest пункт выдачи заказов
Soonest пункт выдачи заказов Глобальная сеть интернет
Глобальная сеть интернет Презентация на тему Древние германцы и Римская империя
Презентация на тему Древние германцы и Римская империя  AIESEC
AIESEC  Решение логических задач на олимпиадах по обществознанию (методические указания и комментарии к оцениванию)
Решение логических задач на олимпиадах по обществознанию (методические указания и комментарии к оцениванию) ALTA Personnel Pharma & Medical Equipment
ALTA Personnel Pharma & Medical Equipment Осложнения интубации трахеи
Осложнения интубации трахеи А. С. Грибоедов
А. С. Грибоедов Порядок начисления простых процентов. Лекция 2
Порядок начисления простых процентов. Лекция 2 Курсовая работа на тему: В стране выученных уроков
Курсовая работа на тему: В стране выученных уроков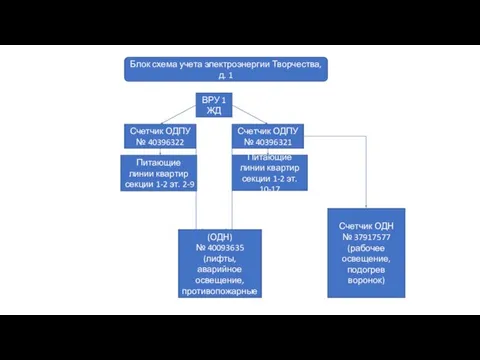 блок схема Творчества, д. 1
блок схема Творчества, д. 1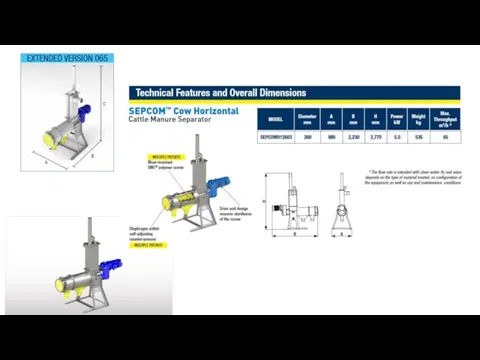 Solid Separator
Solid Separator Результативность системы воспитания детей и молодежи Великого Новгорода
Результативность системы воспитания детей и молодежи Великого Новгорода Тонкая палитра оттенков
Тонкая палитра оттенков инъекции
инъекции Внеклассные мероприятия на основе православных традиций
Внеклассные мероприятия на основе православных традиций Информатизация школьного образовательного пространства
Информатизация школьного образовательного пространства