Sootvetstvia_mezhdu_mnozhestvami_Lektsia-2

Понятие соответствия
Студентам 104 группы факультета начального образования Анастасии, Николаю, Марии, Елене был задан вопрос: занимаются ли они такими видами спорта, как волейбол, шахматы, плавание, теннис и гимнастика? Их ответы поместили в таблицу:

Соответствие между множествами Х и Y мы установили, имея три множества: множество Х – имен студентов, множество Y – названий видов спорта и подмножество декартова произведения X x Y.
Обозначим это подмножество буквой G и перечислим его элементы: G = {(Анастасия, волейбол), (Анастасия, теннис), (Николай, плавание), …}.

Соответствием между множествами X и Y (или соответствием из X в Y) называется любое подмножество декартова произведения XxY.
Множество Х называют множеством отправления соответствия, множество Y – множеством прибытия соответствия, а множество G ХхY.

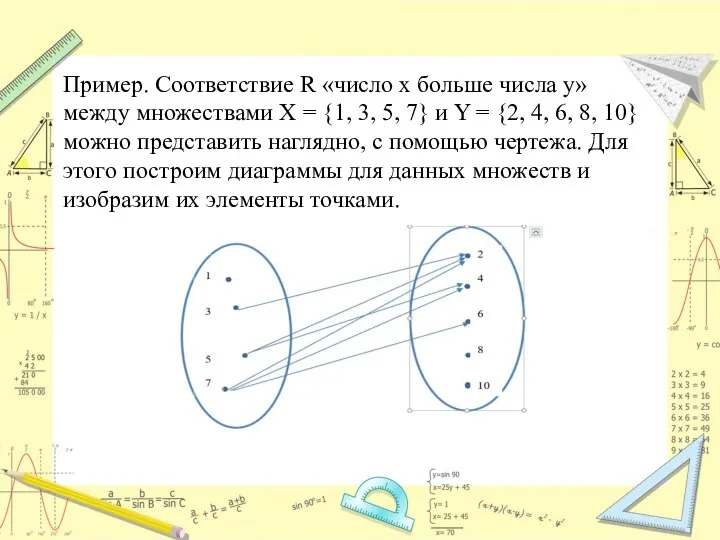
Пример. Соответствие R «число х больше числа y» между множествами Х = {1, 3, 5, 7} и Y = {2, 4, 6, 8, 10} можно представить наглядно, с помощью чертежа. Для этого построим диаграммы для данных множеств и изобразим их элементы точками.

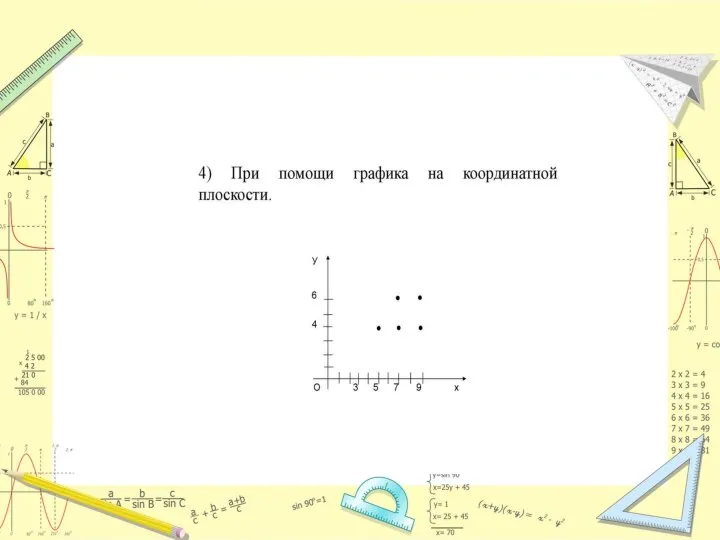
В начальной школе
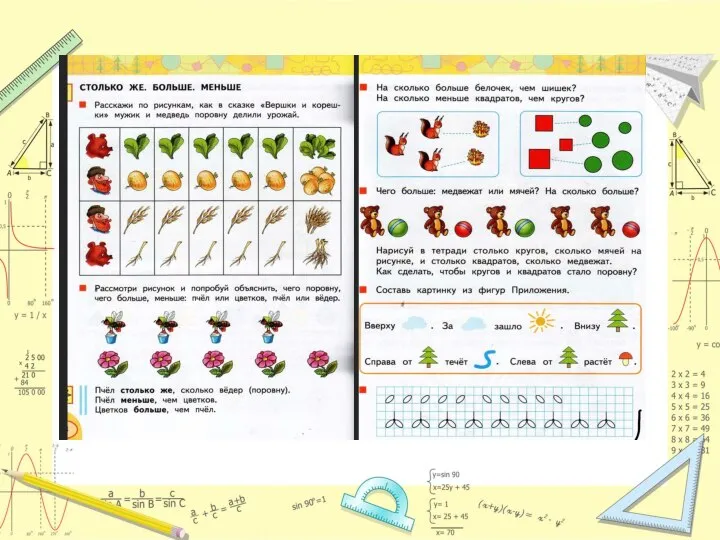
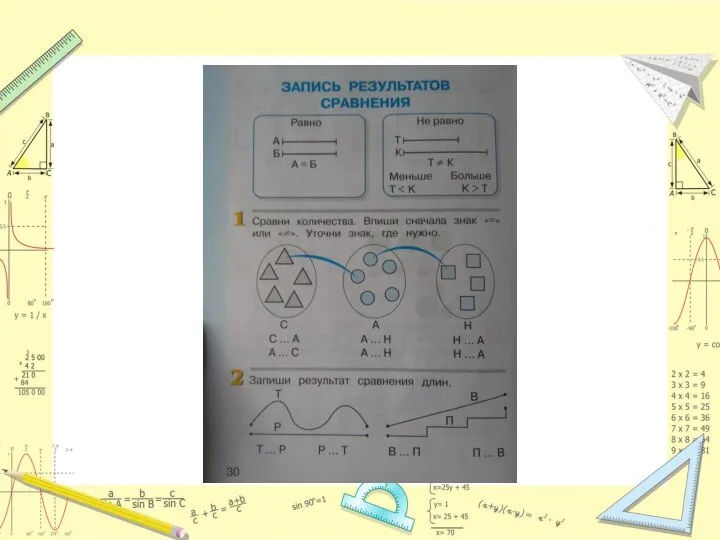
В начальном курсе математики взаимно однозначные соответствия изучаются до изучения чисел: учащихся учат сравнивать предметные множества по их численности. Суть приема: если между множествами можно установить взаимно однозначное соответствие, то в одном множестве элементов СТОЛЬКО ЖЕ, сколько в другом. Если взаимно однозначное соответствие устанавливается между одним множеством и собственным подмножеством другого, то в первом множестве элементов МЕНЬШЕ, чем во втором (во втором множестве элементов БОЛЬШЕ, чем в первом).

Множество Х называется бесконечным, если оно содержит собственное подмножество,
равномощное всему множеству Х.
Натуральное число – класс конечных равномощных множеств