Создание программ-функций в среде MathCAD

Реализовать тот или иной алгоритм вычисления в среде MathCAD можно двумя способами:
1 способ:
размещать обращение к соответствующим переменным, выражениям, операторам, функциям непосредственно в тексте документа MathCAD без какой-либо организационной структуры; данный способ называется программированием в тексте документа;
2 способ:
использовать организационные структуры, так называемые программы-функции, которые содержат конструкции, во многом подобные конструкциям таких языков программирования высокого уровня как FORTRAN, Pascal, С++, С# и др.
В данной лекции будем рассматривать второй способ реализации алгоритмов, который называется программированием в программе-функции.

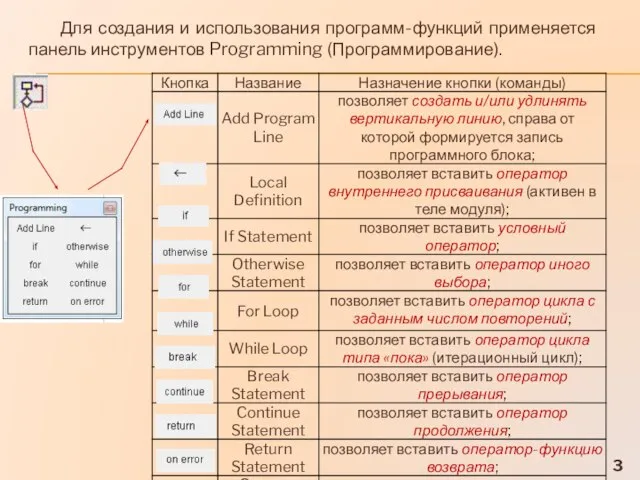
Для создания и использования программ-функций применяется панель инструментов Programming (Программирование).

Примеры программ-функций:

Процесс программирования в программе-функции включает в себя два этапа:
описание программы-функции;
обращение к программе-функции (вызов).
Описание программы – функции размещается в рабочем документе перед вызовом программы-функции и имеет следующую структуру:
имя функции
имена формальных параметров
тело программы-функции (местозаполнители для ввода операторов)

Обращение к программе-функции (вызов) располагается правее или ниже описания программы-функции и может иметь следующую структуру:
Формат 1.1:
name_function(
)=
Формат 1.2:
name_var := name_function(
)
name_var =
с использованием фактических параметров
Формат 2.1:
name_function=
Формат 2.2:
name_var := name_function
name_var =
без использования фактических параметров

Между формальными и фактическими параметрами должно быть установлено взаимно-однозначное соответствие по:
name_function(
)=
количеству;
порядку следования;
типу.

Варианты обращений к программе-функции, реализующей итерационную процедуру приближенного вычисления корня квадратного из числа а:
1
2
3

В реализации алгоритмов линейной структуры в программах-функциях используется оператор внутреннего присваивания (локальный оператор присваивания), с помощью которого осуществляется внутри программы-функции присваивание значений (числовых, строковых) переменным.
< имя_переменной > ← < выражение >
Формат оператора:
Замечание: использование "обычного" оператора присваивания ( : = ) в теле программы-функции приводит к синтаксической ошибке.
выражение, определяющее возвращаемое через имя программы-функции значение
Линейный алгоритм (следование) - вычислительный процесс, в котором необходимые действия выполняются строго последовательно и каждое один раз.

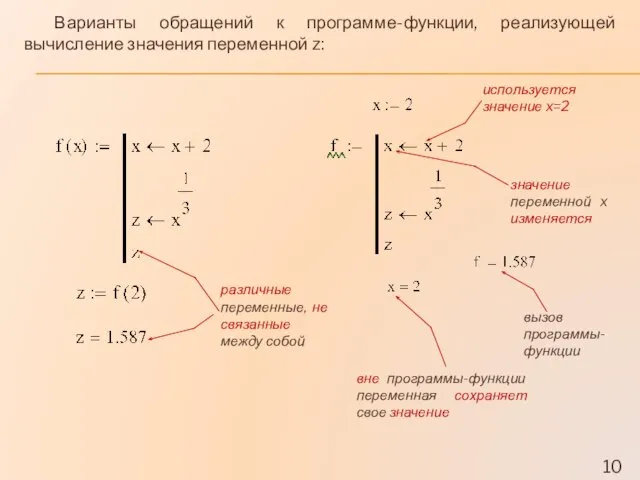
различные переменные, не связанные между собой
вне программы-функции переменная сохраняет свое значение
используется значение x=2
значение переменной x изменяется
вызов программы-функции
Варианты обращений к программе-функции, реализующей вычисление значения переменной z:

Пример 1. Написать программу-функцию, вычисляющую значения корней квадратного уравнения ax2 + bx +c = 0.
Пример 2. Написать программу-функцию, вычисляющую произведение цифр четырехзначного положительного целого числа N.
Примечание к примеру 2: для решения задачи следует использовать функции:
mod(x,y) – возвращает остаток при делении числа x на y (x и y – действительные числа, результат наследует знак числа x) ;
trunc(x) – возвращает целую часть действительного числа x.

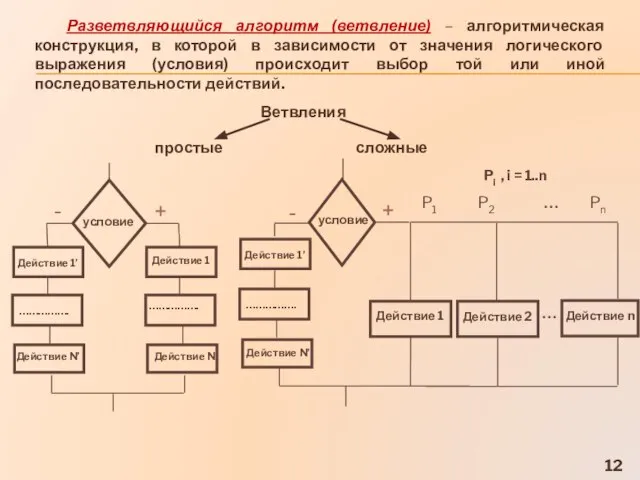
Разветвляющийся алгоритм (ветвление) – алгоритмическая конструкция, в которой в зависимости от значения логического выражения (условия) происходит выбор той или иной последовательности действий.
Ветвления
простые сложные
условие
Действие 1
+
-
…………….
Действие N
Действие 1’
…………….
Действие N’
Pi , i = 1..n

Для реализации ветвлений в программах-функциях используется:
условная функция if (встроенная функция системы MathCAD);
условный оператор If Statement и оператор иного выбора Otherwise Statement (с панели инструментов Программирование) .
Условие (логическое выражение)
простое сложное
результаты вычисления логического выражения
Следует отметить, что при формировании сложных условий вместо операторов And, Or могут быть также использованы арифметические операторы сложения и умножения:

Пример 3. Написать программу-функцию, определяющую принадлежность точки с координатами x и y заштрихованной области на рисунке.
if ( < логич. выраж. > , < ариф.выраж.1> , < ариф.выраж.2 > )
Формат условной функции if:
Внутри программы-функции условная функция используется в арифметических выражениях, стоящих в правой части локального оператора присваивания (оператора внутреннего присваивания).
Решение: заштрихованная область – это точки, удовлетворяющие системе неравенств:

Формат использования
условного оператора if и оператора иного выбора Otherwise
поле для ввода логического выражения
поле для ввода выражения, значение которого используется, если значение логического выражения true
Данные операторы могут находиться только внутри тела программы-функции!
поле для ввода выражения, значение которого используется, если значение логического выражения false

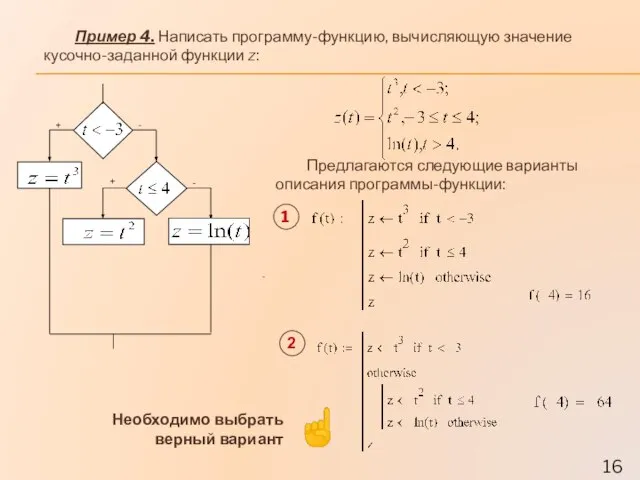
Пример 4. Написать программу-функцию, вычисляющую значение кусочно-заданной функции z:
-
Предлагаются следующие варианты описания программы-функции:
1
2
Необходимо выбрать верный вариант
☝

Циклический алгоритм (цикл) - алгоритмическая конструкция, которая содержит упорядоченную совокупность действий, повторяющихся многократно.
Циклы можно условно разделить на две группы:
циклы типа арифметической прогрессии (с заданным числом повторений), реализуются с помощью оператора for;
итерационные циклы, реализуются с помощью оператора while.
Формат использования оператора for
поле для диапазона изменений параметра
поле для ввода тела цикла
поле для ввода параметра цикла
диапазон изменений параметра формируется с помощью ранжированной переменной
добавление полей с помощью Add Line

Пример 5. Табулирование функции одной переменной y=f(x) на отрезке [a;b] с шагом h.
Для решения задачи необходимо найти значения заданной функции в каждом узле получившейся совокупности точек и представить их в виде таблицы.

Конкретизируем постановку задачи: на отрезке от -2 до 2 с шагом 0,5 протабулировать функцию f(x) = e-x . Cos ( 2x ).
<описание программы-функции>
отображается значение y0=0, т.к. значение системной переменной ORIGIN по умолчанию равно 0

Формат использования оператора while:
поле для ввода тела цикла
поле для ввода логического выражения
добавление полей с помощью Add Line
Для итерационных циклов нельзя априори определить количество повторений тела цикла. Это обусловлено тем, что окончание таких циклов определяется не выходом параметра цикла за конечное значение, а более сложными условиями.

Пример 6. Вычислить приближенное значение корня квадратного , используя итерационную процедуру:
, где
Известно, что в качестве приближенного значения корня квадратного берется такое значение xn, которое удовлетворяет условию

Формат использования оператора прерывания break:
поле для ввода логического выражения
поле для ввода оператора, выполняемого если значение лог. выражения false
прерывание цикла, если значение логического выражения true
значение ierr