Средняя школа 46 ШЕСТЬ УРОКОВ ПО КОМБИНАТОРИКЕ В 7-м КЛАССЕ Белгород 2005 Тарасова А.М.

Область математики, в которой изучают комбинаторные задачи, называется комбинаторикой
Задачи, в которых идет речь о всевозможных комбинациях объектов, называются комбинаторными задачами
УРОК №1. Введение в комбинаторику

Задача. Путешественник хочет выехать из города А, посетить города В,С и D, после чего вернуться в город А. Какими путями можно это сделать?
УРОК №1

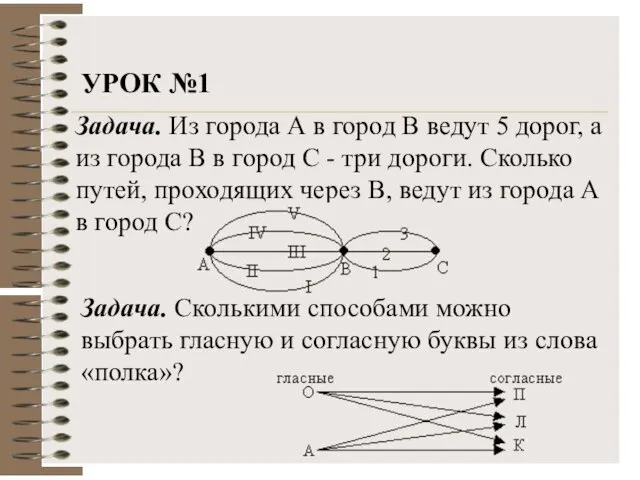
Задача. Из города А в город В ведут 5 дорог, а из города В в город С - три дороги. Сколько путей, проходящих через В, ведут из города А в город С?
Задача. Сколькими способами можно выбрать гласную и согласную буквы из слова «полка»?
УРОК №1

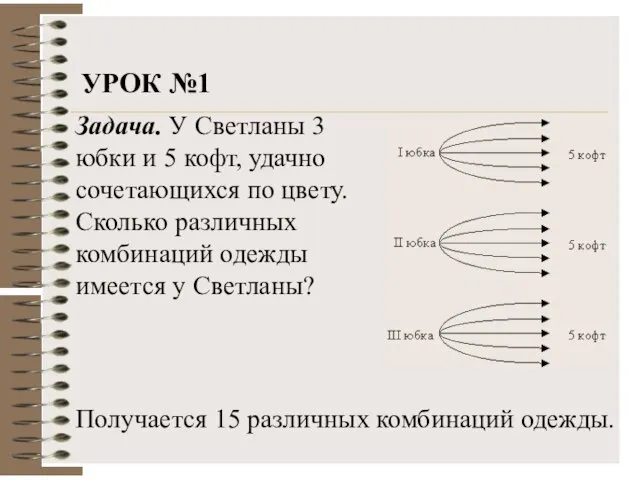
Задача. У Светланы 3 юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций одежды имеется у Светланы?
Получается 15 различных комбинаций одежды.
УРОК №1

Задача. Начальник пригласил несколько человек на совещание. Каждый участник совещания, входя в кабинет, пожимал руки всем присутствующим. Сколько человек участвовало в совещании, если было всего 78 рукопожатий? Задача. На дискотеку собрался почти весь класс – 22 человека. Лена танцевала с семью мальчиками, Нина – с восьмью, Вера – с девятью и т.д. до Ирины, которая танцевала со всеми мальчиками из этого класса. Сколько мальчиков было в этом классе?
УРОК №1

Устные упражнения.
В киоске продают 5 видов конвертов и 4 вида марок. Сколькими способами можно купить конверт и марку?
2. Изменяя порядок слов, составьте предложения: «Я мою руки».
3. Разложите на простые множители число 30. Сколькими способами можно записать в виде простых множителей число 30?
УРОК №2. Факториал

Определение.
Произведение первых n натуральных чисел, т.е. 1• 2 • 3 •…• n называют «n-факториал» и обозначают n! 1•2•3•…•n=n! («эн факториал»)
Например, 4! = 1•2•3•4=24
Главное свойство факториала следует из определения:
(n+1)!=(n+1)•n!
Подставим в эту формулу n=0.
Получим: 1!=1•0!, откуда 0!=1
УРОК №2

УРОК №2

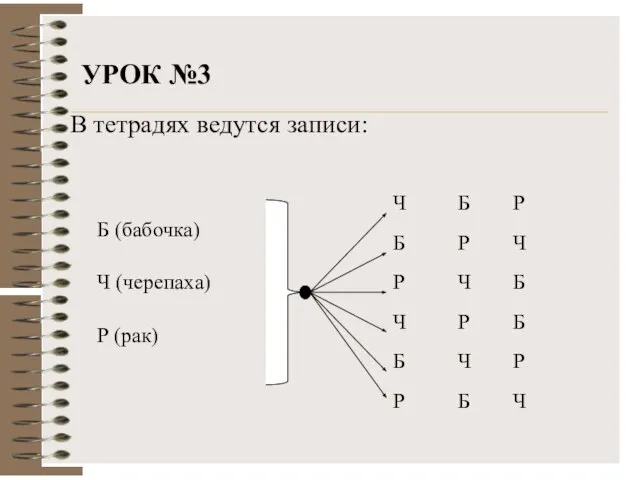
УРОК №3. Перестановки
Пусть элементами будут бабочка, черепаха и рак. Составим всевозможные соединения, которые отличаются порядком расположения элементов.

УРОК №3
В тетрадях ведутся записи:

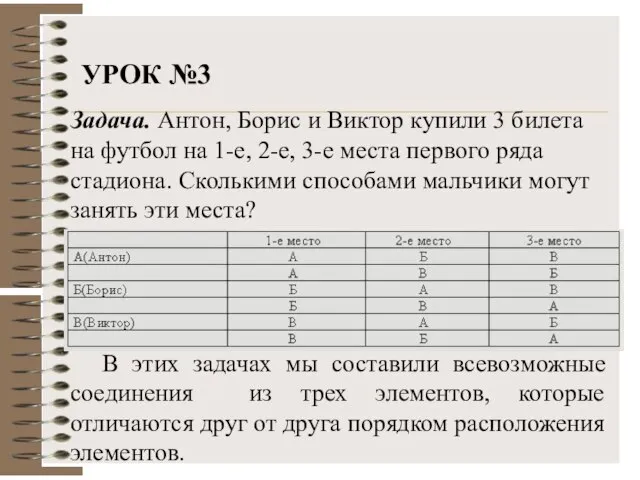
УРОК №3
Задача. Антон, Борис и Виктор купили 3 билета на футбол на 1-е, 2-е, 3-е места первого ряда стадиона. Сколькими способами мальчики могут занять эти места?
В этих задачах мы составили всевозможные соединения из трех элементов, которые отличаются друг от друга порядком расположения элементов.

УРОК №3
Определение.
Комбинации из n-элементов, отличающиеся друг от друга только порядком расположения в них элементов, называются перестановками из n элементов.
Перестановки из n элементов обозначают Pn и вычисляют по формуле
Pn=n!(пэ из эн).
Например, Р3=6, 3!=1•2•3=6

УРОК №3
7) Сколько различных чисел можно составить из цифр 0, 1, 2, 3, 4 при условии, что в каждом из этих чисел все цифры различны?
Решение.
Р5 =5! =120 .
Так как число не может начинаться нулем, то надо вычесть количество чисел, первая цифра которых 0, Таких чисел будет Р4=4!=24.
Р5-Р4=120-24=96. Ответ: 96 чисел.

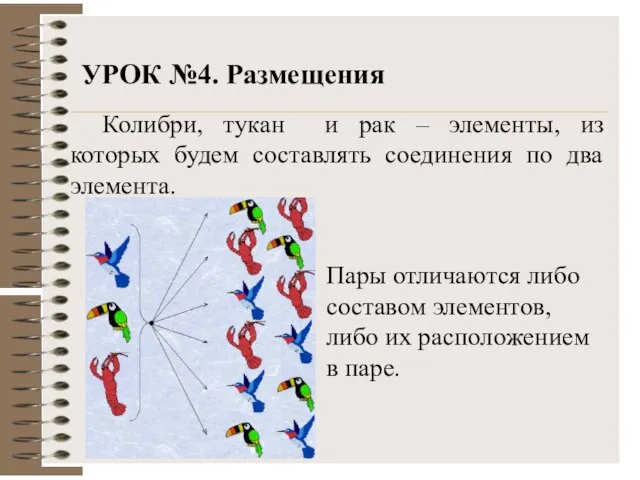
УРОК №4. Размещения
Колибри, тукан и рак – элементы, из которых будем составлять соединения по два элемента.
Пары отличаются либо составом элементов, либо их расположением в паре.

УРОК №4
Задача. Антон, Борис и Виктор приобрели два билета на футбольный матч на 1-е и 2-е места первого ряда стадиона. Сколько существует способов занять эти два места на стадионе?
Решение.
А(Антон) 1. А Б, 2.А В, 3.Б В .
Б (Борис)
В(Виктор)
(Если мальчики будут пересаживаться со своего места на место друга, то таких соединений будет 6).

УРОК №4
Определение.
Комбинации из n элементов по k, отличающиеся друг от друга либо составом элементов, либо порядком их расположения, называются размещениями из n элементов по k.
Полученные пары называются размещениями из трех элементов по два.

УРОК №4
*Сколько надо взять элементов, чтобы число размещений из них по четыре было в 12 раз больше, чем число размещений из них по два?
Решение.
Пусть надо взять n элементов, тогда Аn4 =12⋅Аn2,
…
n2-5n-6=0
(учащиеся 7-го класса представят 5n в виде суммы двух слагаемых);
n2+n-6n-6=0,
n (n+1)-6 (n+1)=0,
(n+1)(n-6) =0,
n = -1, n=6.
По смыслу задачи n=6.

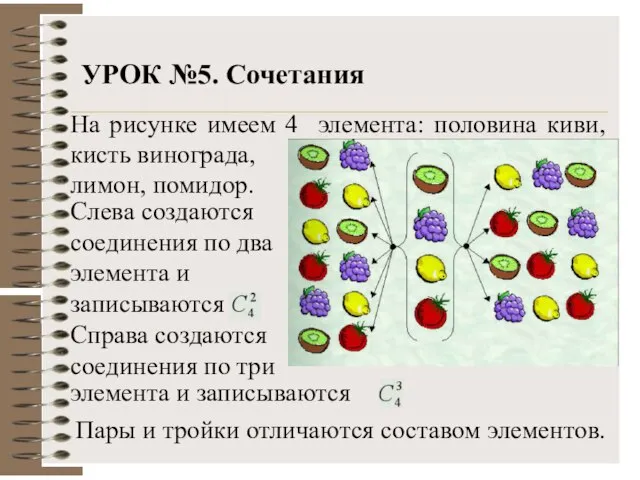
УРОК №5. Сочетания
На рисунке имеем 4 элемента: половина киви, кисть винограда,
лимон, помидор.
Слева создаются соединения по два элемента и записываются Справа создаются соединения по три
элемента и записываются
Пары и тройки отличаются составом элементов.

УРОК №5
Определение.
Комбинации из n элементов по k , отличающиеся друг от друга лишь составом элементов, называются сочетаниями из n элементов по k. (k≤n).
Записывают и читают это так: (сочетания из n элементов по k).
Количество сочетаний можно посчитать по формуле

УРОК №6. Контрольная работа
Вариант 1
1. Найти:
2. Задача.
У лесника 3 собаки Астра (А), Вега (В) и Гриф(Г). На охоту лесник решил пойти с двумя собаками. Перечислить все варианты выбора лесником пары собак.
Сделать рисунок. Посчитать по формуле.

УРОК №6
3.Задача.
Сколькими способами 4 различных монеты можно разместить по двум карманам?
4. Задача.
В классе 35 учеников. 20 из них занимаются в математическом кружке, 11-в биологическом, а 10 ничем не занимаются. Сколько ребят занимаются и математикой, и биологией?

УРОК №6
Вариант 2
1. Найти :А57+Р5.
2. Задача.
Из трёх стаканов сока ананасового (а), брусничного (б) и виноградного(в)-Иван решил выпить последовательно два. Перечислить все способы , которыми это можно сделать.
Сделать рисунок. Посчитать по формуле.