Standard deviation

Total: 22
Example: The mid-day temperatures (in °C) recorded for one week in June were: 21, 23, 24, 19, 19, 20, 21
Standard deviation
So variance = 22 ÷ 7 = 3.143
So, s.d. = 1.77°C (3 s.f.)
°C
First we find the mean:

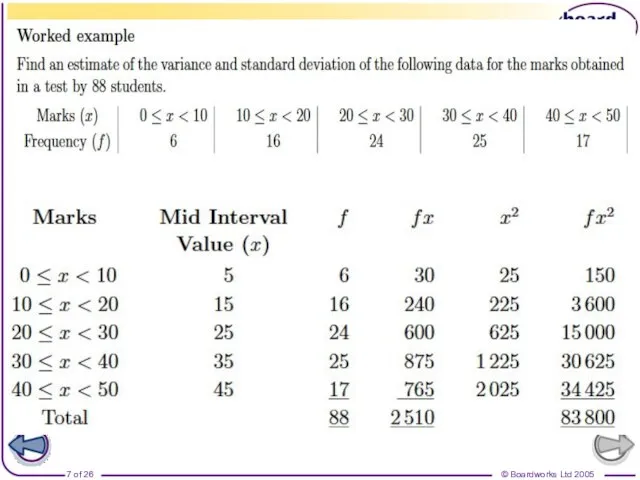
There is an alternative formula which is usually a more convenient way to find the variance:
Standard deviation
Therefore, and

Example (continued): Looking again at the temperature data for June: 21, 23, 24, 19, 19, 20, 21
Standard deviation
°C
Also, = 3109
°C
Note: Essentially the standard deviation is a measure of how close the values are to the mean value.
We know that
So,

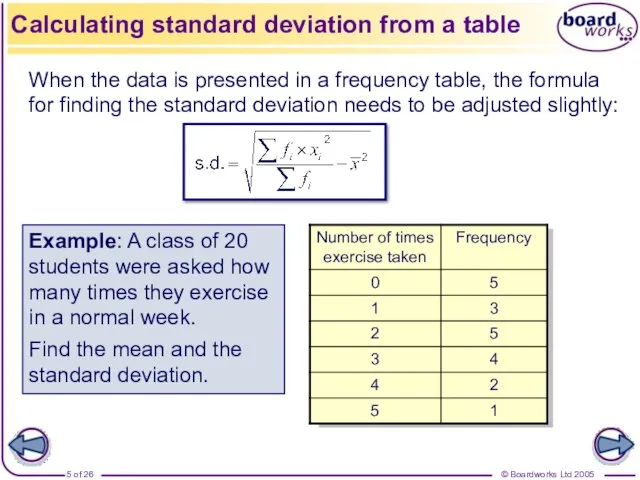
When the data is presented in a frequency table, the formula for finding the standard deviation needs to be adjusted slightly:
Calculating standard deviation from a table
Example: A class of 20 students were asked how many times they exercise in a normal week.
Find the mean and the standard deviation.

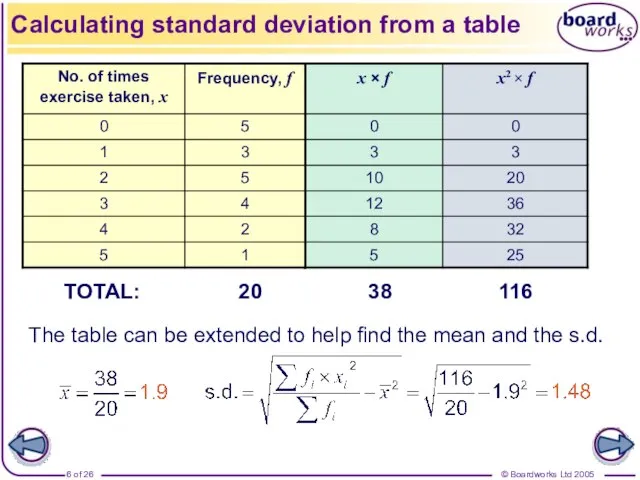
Calculating standard deviation from a table
The table can be extended to help find the mean and the s.d.
TOTAL: 20 38 116