Статика

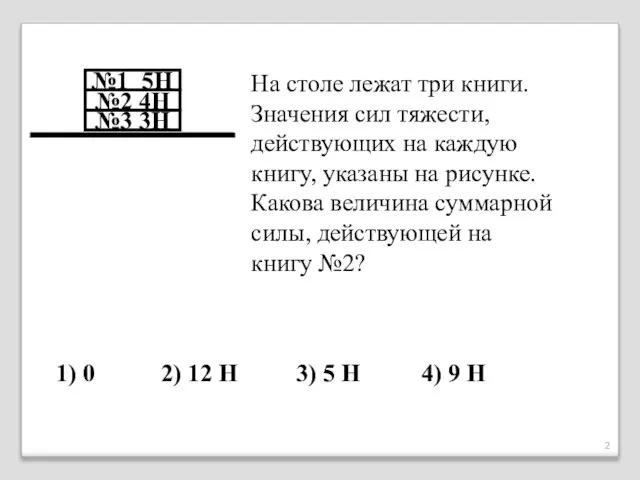
На столе лежат три книги. Значения сил тяжести, действующих на каждую книгу, указаны на рисунке. Какова величина суммарной силы, действующей на книгу №2?
1) 0
2) 12 Н
3) 5 Н
4) 9 Н

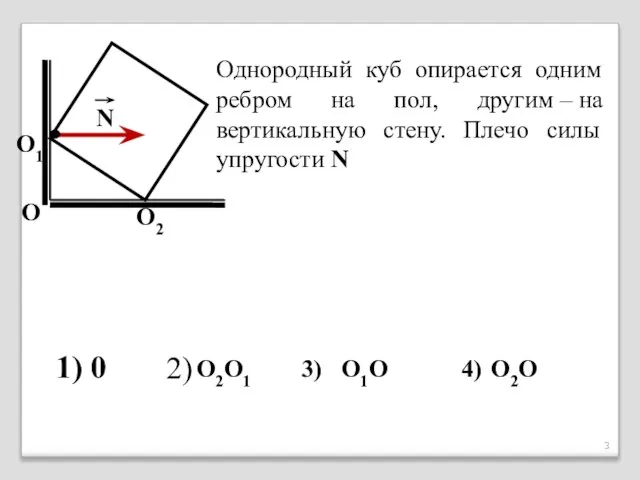
Однородный куб опирается одним ребром на пол, другим – на вертикальную стену. Плечо силы упругости N
2)
О2О1
3)
О1О
4)
О2О
1) 0

Труба массой М = 1 т лежит на земле. Какую силу (в кН) надо приложить, чтобы приподнять краном трубу за один из ее концов?
1) 10 кН
3) 15 кН 4) 20 кН
2) 5 кН

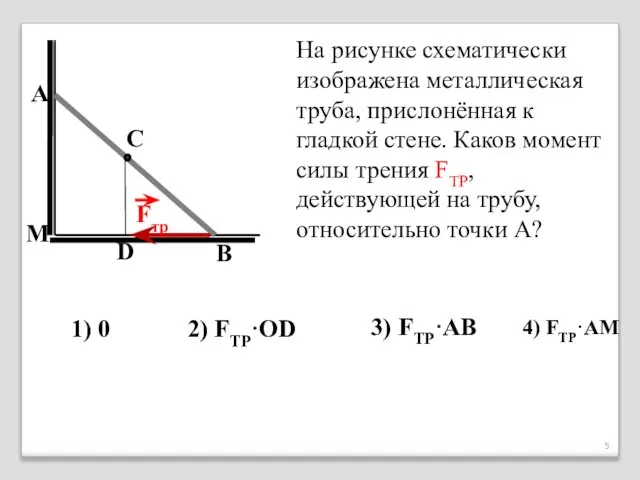
На рисунке схематически изображена металлическая труба, прислонённая к гладкой стене. Каков момент силы трения FTP, действующей на трубу, относительно точки A?
1) 0
2) FТР·OD
3) FТР·AB
4) FТР·AM

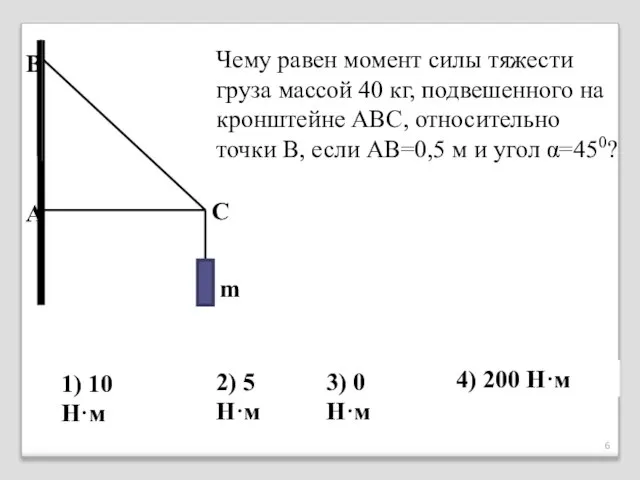
Чему равен момент силы тяжести груза массой 40 кг, подвешенного на кронштейне АВС, относительно точки В, если АВ=0,5 м и угол α=450?
1) 10 Н·м
2) 5 Н·м
3) 0 Н·м
4) 200 Н·м

При решении задач на равновесие тел:
Сделать рисунок, показать все силы, действующие на тело (или тела системы),находящиеся в положении равновесия, выбрать систему координат и определить направление координатных осей.
2. Для тела, не имеющего оси вращения, записать первое условие равновесия в векторной форме ∑F = 0, затем записать это условие равновесия в проекциях на оси координат и получить уравнение в скалярной форме.
3. Для тела, с закрепленной осью вращения, следует определить плечи всех сил относительно этой оси и использовать второе условие равновесия (правило моментов): ∑М = 0.Если из условия задачи следует, что ось вращения тела не закреплена, то необходимо использовать оба условия равновесия. При этом положение оси вращения следует выбирать так, чтобы через нее проходило наибольшее число линий действия неизвестных сил.
4. Решить полученную систему уравнений и определить искомые величины.

К гвоздю, вбитому в стенку, привязана нить, намотанная на катушку. Катушка висит, касаясь стенки, как показано на рисунке. Радиус оси катушки r = 0,5 см, радиус ее щечек R = 10 см. Коэффициент трения между стенкой и катушкой μ = 0,1. При каком угле α между нитью и стенкой катушка висит неподвижно?
Задача №1
α
решение

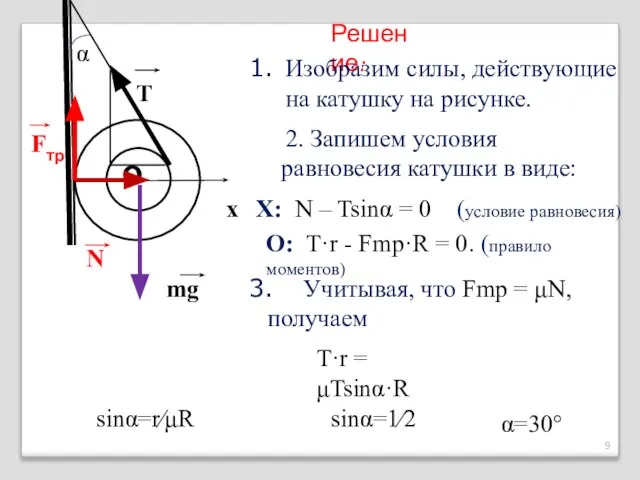
Решение:
Изобразим силы, действующие на катушку на рисунке.
mg
N
Fтр
T
2. Запишем условия равновесия катушки в виде:
x
X: N – Tsinα = 0 (условие равновесия)
α
О: T·r - Fmp·R = 0. (правило моментов)
Учитывая, что Fmp = μN,
получаем
T·r = μTsinα·R
sinα=1⁄2
α=30°
sinα=r⁄μR

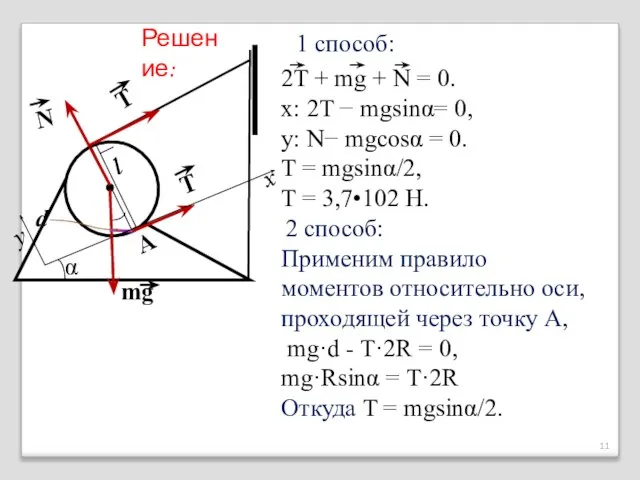
Цилиндр массой m = 150 кг удерживается на наклонной плоскости с помощью ленты, с одной стороны закрепленной на наклонной плоскости, а с другой направленной параллельно плоскости. Найти силу натяжения ленты. Угол наклона плоскости α = 30°.
Задача №2
α
A
R
решение

2T + mg + N = 0.
x: 2T − mgsinα= 0,
y: N− mgcosα = 0.
T = mgsinα/2,
T = 3,7•102 H.
x
y
1 способ:
2 способ:
Применим правило моментов относительно оси, проходящей через точку A,
mg·d - T·2R = 0,
mg·Rsinα = T·2R
Откуда T = mgsinα/2.
Решение:

Задача №3
Однородный шар радиуса R подвешен на нити длиной ℓ, конец которой закреплен на вертикальной стене . Точка крепления к шару находится на одной вертикали с центром шара. Каков должен быть коэффициент трения между шаром и стеной, чтобы шар находился в равновесии?
решение

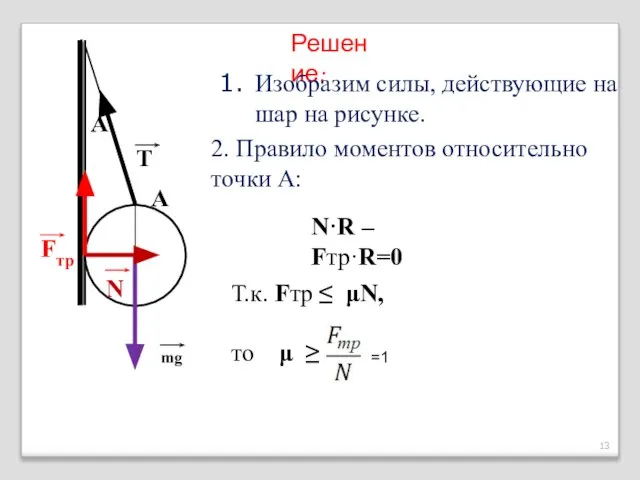
mg
N
Fтр
T
Α
Решение:
А
2. Правило моментов относительно
точки А:
N·R – F‪тр·R=0
Изобразим силы, действующие на шар на рисунке.
=1

Задача №4.
Какой минимальной горизонтальной силой можно опрокинуть через ребро куб, лежащий на горизонтальной плоскости?
F
решение

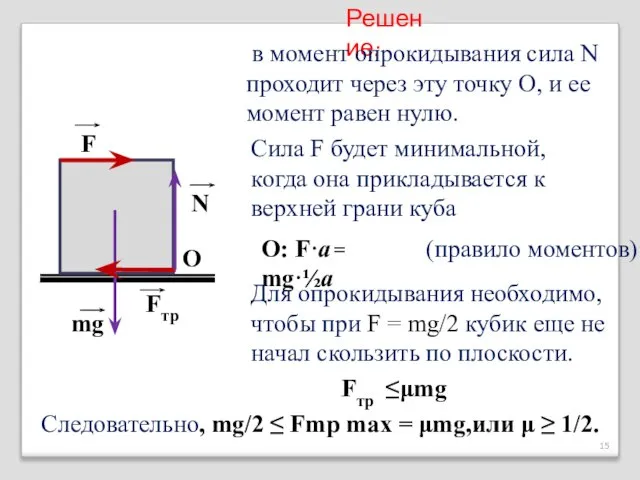
F
O
mg
Fтр
N
Решение:
в момент опрокидывания сила N проходит через эту точку О, и ее момент равен нулю.
Сила F будет минимальной, когда она прикладывается к верхней грани куба
О: F·a= mg·½а
Для опрокидывания необходимо, чтобы при F = mg/2 кубик еще не начал скользить по плоскости.
Следовательно, mg/2 ≤ Fmp max = μmg,или μ ≥ 1/2.
(правило моментов)

Тонкостенная полусфера массой M и радиусом R покоится на горизонтальном столе. На какую высоту опустится край полусферы, если на него сядет муха массой m ? Центр тяжести полусферы расположен на расстоянии a=½R от ее центра.
решение
Задача №5.

Решение:
Под действием веса мухи полусфера займет наклонное положение
Уравнение моментов, записанное относительно оси, перпендикулярной плоскости рисунка и проходящей через точку А:
Сл.,

Домашнее задание:
Л.А.Кирик. Работа №25(дост. ур.7,8 ; выс.ур.1,2)