СТАТИСТИЧЕСКИЕ МЕТОДЫ АНАЛИЗА СВЯЗИ

Признаки, которыми характеризуются единицы совокупности, могут быть взаимосвязанными. Взаимосвязанные признаки могут выступать в одной из ролей:
- роли признака-результата (аналог зависимой переменной (Y) в математике);
роли признака-фактора, (аналог независимой переменной (X) в математике). Значение признака-фактора определяют значение признака-результата
Связи в статистике классифицируют по степени тесноты, направлению, форме, числу факторов.

По степени тесноты связи делят на статистические и функциональные.
Статистическая (стохастическая) связь – это такая связь между признаками, при которой для каждого значения признака-фактора Х
признак-результат Y может в определенных пределах принимать любые значения
с некоторыми вероятностями;
при этом его статистические (обобщающие) характеристики (например, среднее значение) изменяются по определенному закону.
· · х
х1 х2 х3 х4 х5
у ·
· ·
· · ·
· · ·

Корреляционная связь частный случай стохастической связи. При корреляционной связи с изменением значения признака Х среднее значение признака Y закономерно (функционально) изменяется.
Модель стохастической связи может быть представлена в общем виде уравнением: y=f(х)+u,
где f(x) - часть результативного признака, сформировавшаяся под воздействием фактора x;
u - случайная составляющая, часть результативного признака, являющаяся результатом действия прочих (неучтенных) факторов, а также ошибок измерения признаков.

Функциональная связь – такая связь, при которой для каждого значения признака-фактора
признак-результат принимает одно (иногда несколько) строго определенных значений.
Она имеет место, когда все факторы, действующие на результативный признак, известны и учтены в модели и ошибки измерения отсутствуют.
Модель функциональной связи может быть представлена как: y=f(х).
у
·
·
·
· х
х1 х2 х3 х4

По направлению связи делят на прямые и обратные связи.
При прямой связи направление изменения результата совпадает с направлением изменения признака-фактора.
При обратной связи направление изменения результата противоположно направлению изменения признака-фактора.
Например, чем выше квалификация рабочего, тем выше уровень производительности его труда (прямая связь). Чем выше производительность труда, тем ниже себестоимость единицы продукции (обратная связь).

По форме связи (виду функции f) связи делят на линейные (прямолинейные) и нелинейные (криволинейные) связи.
Линейная связь отображается прямой линией; криволинейная отображается кривой (параболой, гиперболой и т.п.).
При линейной связи с увеличением на единицу значения признака-фактора происходит равномерное возрастание (убывание) значения признака-результата.
При криволинейной связи с увеличением на единицу значения признака-фактора возрастание (убывание) признака-результата происходит неравномерно (гиперболическая форма связи) или же меняется направление связи (параболическая форма связи).

По количеству факторов, действующих на результат, связи подразделяют на однофакторные (парные) и многофакторные связи.

Порядок изучения парной статистической связи:
1. Качественный (содержательный) анализ связи. На этом этапе производят предварительный анализ направления и формы связи.
2. Сбор данных (статистическое наблюдение).
3. Эмпирический анализ связи.
4. Количественная оценка тесноты связи (корреляционный анализ).
5. Установление аналитической зависимости между признаками (регрессионный анализ):
5.1. выбор формы связи (вида аналитической зависимости);
5.2. оценка параметров уравнения регрессии;
5.3. оценка качества уравнения регрессии.

3 этап – эмпирический анализ связи
состоит в построении группировок (аналитической или комбинационной) и графиков.
Для анализа связи между признаками служат графики: корреляционное поле и эмпирическая линия регрессии.
Корреляционное поле – точечный график, построенный в системе координат Х, Y. Число точек равно числу единиц в совокупности. Каждая точка соответствует некоторой единице совокупности и имеет координаты по оси абсцисс – значение признака-фактора Х, а по оси ординат – значение признака-результата Y.

Эмпирическая линия регрессия - ломанная линия, построенная по данным аналитической группировки. Число точек ломанной равно числу групп в аналитической группировке. Каждая точка имеет абсциссу равную среднему значению признака-фактора в группе и ординату равную среднему значению признака-результата в этой же группе.
Форма графиков позволяет делать выводы о направлении, форме и тесноты связи.

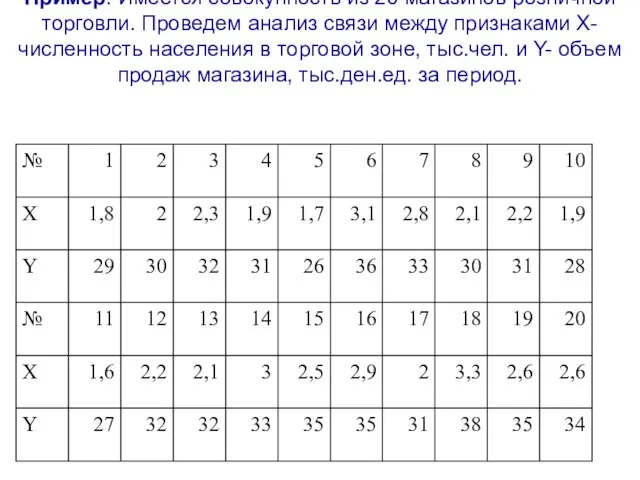
Пример: Имеется совокупность из 20 магазинов розничной торговли. Проведем анализ связи между признаками Х- численность населения в торговой зоне, тыс.чел. и Y- объем продаж магазина, тыс.ден.ед. за период.

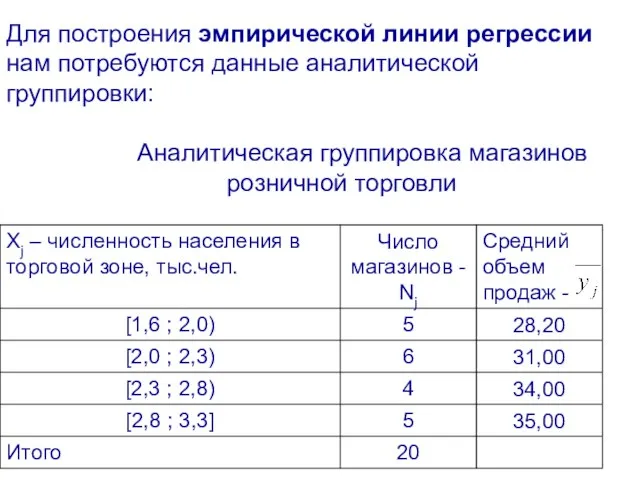
Для построения эмпирической линии регрессии нам потребуются данные аналитической группировки: Аналитическая группировка магазинов розничной торговли

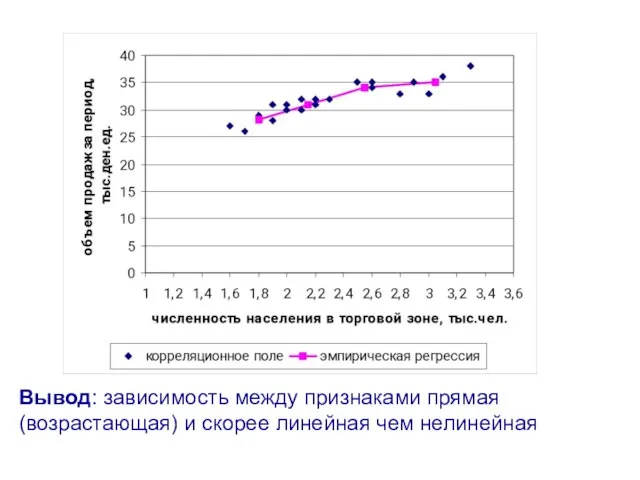
Вывод: зависимость между признаками прямая (возрастающая) и скорее линейная чем нелинейная

4 этап – количественная оценка тесноты связи (корреляционный анализ) состоит в расчете показателей тесноты связи:
эмпирического коэффициента детерминации,
эмпирического корреляционного отношения,
коэффициента Фехнера,
коэффициента линейной парной корреляции.

Эмпирический коэффициент детерминации (эмпирическое дисперсионное отношение) - ρ2.
Данный показатель рассчитывается по данным аналитической группировки, как отношение межгрупповой дисперсии к общей (на основе теоремы о сложении дисперсий):
Эмпирический коэффициент детерминации показывает процент (долю) вариации признака-результата, обусловленную признаком-фактором, положенным в основу группировки.

Межгрупповая дисперсия рассчитывается по формуле :
Остаточная дисперсия рассчитывается по формуле:
Где σ2j – дисперсия признака Y в j-ой группе

Пример: Рассчитаем эмпирический коэффициент детерминации ρ2=δ2y/σ2y для измерения тесноты связи между численностью населения в торговой зоне и объемом продаж магазина розничной торговли по данным аналитической.
Для расчета межгрупповой дисперсии δ2y необходимо знать общее среднее арифметическое значение признака Y. Оно в нашем примере равно:
Тогда межгрупповая дисперсия будет равна:

Общая дисперсия признака Y для нашего примера будет равна:
Тогда эмпирический коэффициент детерминации ρ2=6,95 / 9,09= 0,765
Вывод: 76,5% вариации объема продаж магазина розничной торговли обусловлено численностью населения в торговой зоне.

Эмпирическое корреляционное отношение - ρ.
Данный показатель представляет собой корень из эмпирического коэффициента детерминации. Он измеряет тесноту связи между фактором (группировочным признаком) и результатом. Область допустимых значений эмпирического корреляционного отношения от 0 до +1.
При достаточно тесной связи между признаками эмпирический коэффициент детерминации стремится к 1.
При слабой связи - к нулю.

В нашем примере:
Следовательно, связь между численностью населения в торговой зоне и объемом продаж достаточно тесная.

Коэффициент Фехнера - Кф служит для измерения тесноты линейной связи. Изменяется в пределах от -1 до +1.
Если | Кф |→1 , то связь близка к линейной функциональной. Если признаки х и y взаимно независимы, то |Кф|→0 .
Но равенство нулю коэффициента корреляции означает отсутствие только линейной связи. Если Кф<0,то связь между признаками обратная. Если Кф>0, то связь - прямая.
где С – число совпадений, Н – несовпадений знаков отклонений Х от своего среднего значения и Y от своего среднего значения.

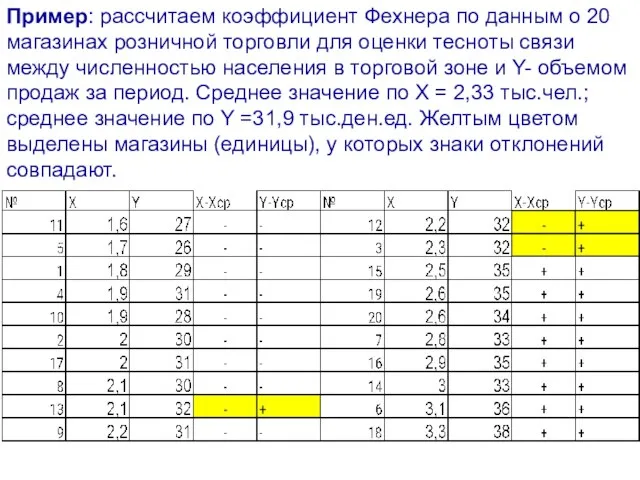
Пример: рассчитаем коэффициент Фехнера по данным о 20 магазинах розничной торговли для оценки тесноты связи между численностью населения в торговой зоне и Y- объемом продаж за период. Среднее значение по Х = 2,33 тыс.чел.; среднее значение по Y =31,9 тыс.ден.ед. Желтым цветом выделены магазины (единицы), у которых знаки отклонений совпадают.

Таким образом число совпадений С=17, число несовпадений равно Н=3.
Следовательно, Кф= (17 - 3) / (17 + 3) = 0,7.
Вывод: так как значение Кф ближе к 1, то связь можно охарактеризовать как достаточно тесную, а положительное значение Кф свидетельствует о прямой зависимости.

Коэффициент линейной парной корреляции используется для оценки степени тесноты линейной связи:
σх, σy - среднее квадратические отклонения признаков Х и Y.
- среднее из произведения

Область допустимых значений линейного коэффициента корреляции от -1 до +1.
Если | rx,y |→1 , то связь близка к линейной функциональной.
Если признаки х и y взаимно независимы, то | rx,y |→0
! Равенство нулю коэффициента корреляции означает отсутствие только линейной связи. Признаки могут быть связаны тесной нелинейной зависимостью и при этом иметь нулевой коэффициент корреляции (например, в случае параболической формы связи).
Если rx,y<0,то связь между признаками обратная.
Если rx,y>0, то связь - прямая.

Пример: рассчитаем коэффициент линейной парной корреляции между численностью населения в торговой зоне и Y- объемом продаж по данным о 20 магазинах розничной торговли.
Вывод: зависимость между признаками объем продаж за период и численность населения в торговой зоне можно характеризовать как очень тесную (r→1) и возрастающую (т.к. r >0).

Если сравнить значения эмпирического корреляционного отношения (ρ) с линейным парным коэффициентом корреляции ( r ), то можно сделать вывод о форме связи.
Если разность ρ - |r| > 0,1, то связь считают нелинейной.
Если данное неравенство не выполняется, то связь считают линейной.
Пример: так как ρ - |r| =0,87 – 0,907 = -0,03 < 0,1 , то связь между признаками объем продаж за период и численность населения в торговой зоне скорее линейная, чем нелинейная.

5 этап - установление аналитической зависимости между признаками (регрессионный анализ)
Регрессия – зависимость среднего значения какой-либо случайной величины от одной или нескольких независимых величин.
Установление аналитической зависимости сводится к построению уравнения регрессии.
Уравнение регрессии – уравнение связи в среднем,
а именно, уравнение, описывающее корреляционную зависимость признака-результата y (его среднего значения) от значения признака-фактора х (или факторов).

Линейное парное (однофакторное) уравнение регрессии имеет вид:
M(yi│x=xi)= f(xi) = а + b·xi ,
где M(yi│x=xi) – условное математическое ожидание зависимой переменной – y при значении независимой переменной x равном хi;
i – номер единицы совокупности (наблюдения), i=1;n,
n - всего наблюдений.
а,b - параметры (коэффициенты) уравнения регрессии.

При построении уравнения регрессии f(x) мы должны:
1) определить вид уравнения (линейное или нелинейное и какое именно нелинейное: парабола, показательное уравнение или другое);
2) оценить параметры регрессии (a, b) по имеющимся данным наблюдений yi, xi.

5.1. Выбор формы связи (вида аналитической зависимости).
Наиболее часто для описания статистической связи признаков используется линейное уравнение регрессии.
Внимание к линейной форме связи объясняется четкой экономической интерпретацией параметров линейного уравнения регрессии,
ограниченной вариацией переменных,
и тем, что в большинстве случаев нелинейные формы связи для выполнения расчетов преобразуют (путем логарифмирования или замены переменных) в линейную форму.

Методы выявления формы связи:
- графический (вид корреляционного поля и эмпирической линии регрессии);
- теоретический анализ и опыт предыдущих аналогичных исследований;
- сравнение эмпирического корреляционного отношения с коэффициентом корреляции;
- перебор всевозможных видов функций и выбор наилучшей по показателю качества.

5.2. Оценки параметров линейной регрессии (а и b) могут быть найдены разными методами: методом наименьших квадратов; методом максимального правдоподобия; методом моментов.
Наиболее распространенным является метод наименьших квадратов (МНК), который при определенных условиях дает наилучшие оценки.

Суть МНК:
Пусть имеются n наблюдений признаков х и y. Причем известен вид уравнения регрессии - f(x) (например, прямолинейная зависимость:
f(хi)=а + b∙хi.
Задача состоит в оценке параметров (а и b), которые подбираются таким образом, чтобы минимизировать сумму квадратов отклонений фактических значений признака-результата yi от расчетных (теоретических) значений f(xi) для всех наблюдений i=1;n :

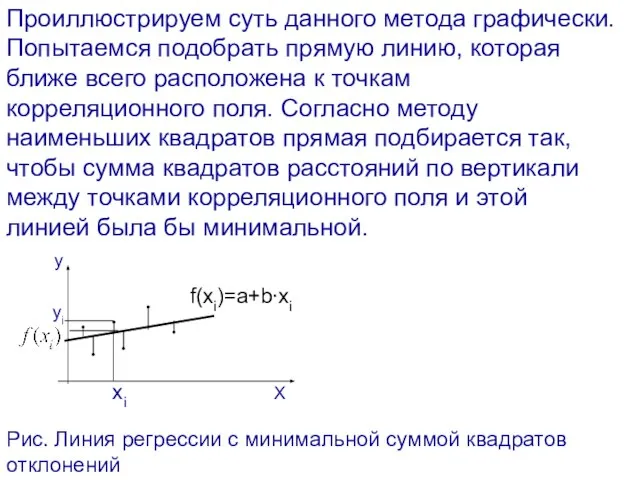
Проиллюстрируем суть данного метода графически. Попытаемся подобрать прямую линию, которая ближе всего расположена к точкам корреляционного поля. Согласно методу наименьших квадратов прямая подбирается так, чтобы сумма квадратов расстояний по вертикали между точками корреляционного поля и этой линией была бы минимальной.
y
yi
xi Х
Рис. Линия регрессии с минимальной суммой квадратов отклонений
f(xi)=a+b∙xi

Значения yi и xi i=1;n нам известны, это данные наблюдений. В функции S они представляют собой константы. Переменными в данной функции являются искомые оценки параметров – а и b .
Чтобы найти минимум функции 2-ух переменных необходимо вычислить частные производные данной функции по каждому из параметров и приравнять их нулю,
т.е. ∂S/∂a = 0 и ∂S/∂b = 0.

В результате получим систему из 2-ух нормальных линейных уравнений:

Решая данную систему, найдем искомые оценки параметров.
Оценка параметра b может быть рассчитана также через коэффициент корреляции:

Знак коэффициента регрессии b указывает направление связи (если b>0, связь прямая, если b<0, то связь обратная).
Величина b показывает на сколько единиц изменится в среднем признак-результат -y при изменении признака-фактора - х на 1 единицу своего измерения.
Формально значение параметра а – среднее значение признака-результата y при нулевом значении х. Если признак-фактор не имеет или не может иметь нулевого значения, то интерпретация параметра а не имеет смысла.

Пример: построим линейное уравнение регрессии объема продаж магазина (y) от значений фактора x– численности населения в торговой зоне:
f(xi)=а+b∙хi, f(xi)-расчетное значение признака y.
Величина b в нашем примере показывает, что при увеличении численности населения в торговой зоне на 1 тыс.чел. объем продаж магазина за период в среднем возрастает (т.к. b>0) на 5,68 тыс.ден.ед.
Значение параметра а не интерпретируется, т.к. нет среди исходных данных значений х равных нулю.

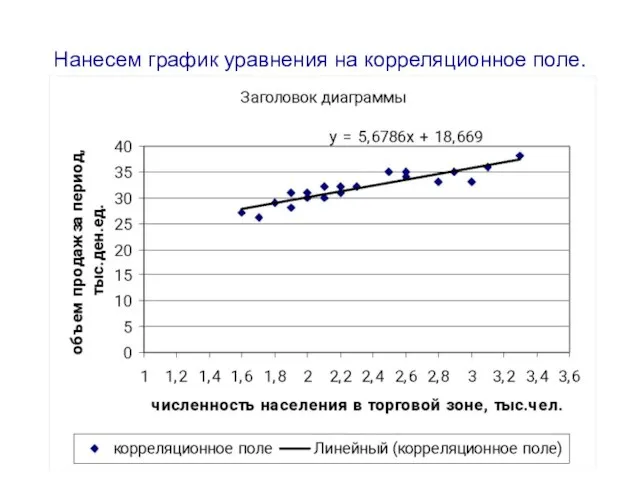
Нанесем график уравнения на корреляционное поле.

5.3. - Оценка качества уравнения регрессии.
Под качеством (адекватностью) уравнения регрессии понимается степень близости (соответствия) рассчитанных по данному уравнению значений признака-результата f(x) фактическим (наблюдаемым) значениям y.
Для оценки качества (адекватности) полученного уравнения регрессии используется ряд показателей:
теоретический коэффициент детерминации;
среднеквадратическую ошибка уравнения регрессии;
средняя ошибка аппроксимации.

Наиболее широкое применение из них получил теоретический коэффициент детерминации – R2.
Данный показатель рассчитывается, как отношение объясненной уравнением дисперсии признака-результата - δ*2, к общей дисперсии признака-результата σ2y :
Объясненная уравнением Необъясненная уравнением
регрессии дисперсия y регрессии дисперсия y

В регрессионном анализе также действует теорема о сложении дисперсий, согласно которой общая дисперсия признака-результата равна сумме объясненной уравнением регрессии дисперсии - δ*2 и остаточной (необъясненной) дисперсии - ε*2 :
σ2y=δ*2 + ε*2. Поэтому коэффициент детерминации может быть также рассчитан через остаточную и общую дисперсии:

Данный показатель (R2) характеризует долю вариации (дисперсии) признака-результата y, объясняемую уравнением регрессии (а, следовательно, и фактором х), в общей вариации (дисперсии) y.
Коэффициент детерминации R2 принимает значения от 0 до 1.
Соответственно величина (1 - R2) характеризует долю дисперсии y, вызванную влиянием прочих неучтенных в уравнении факторов и ошибками измерений.
!! При парной линейной регрессии R2 можно рассчитать по упрощенной формуле: R2=ryx2.

2. Средняя квадратическая ошибка уравнения регрессии представляет собой среднее квадратическое отклонение наблюдаемых значений признака - результата от теоретических значений, рассчитанных по уравнению, т.е.:

Показатели качества (адекватности) используют также для решения задачи выбора вида функциональной зависимости. Выбор может быть осуществлен путем сравнения величин показателя качества (R2 или su), рассчитанных для разных функциональных зависимостей. Чем больше величина коэффициента детерминации R2 (или чем меньше величина среднеквадратической ошибки su), тем уравнение лучше.
Если показатели адекватности оказываются примерно одинаковыми для нескольких функций, то предпочтение отдается более простым видам функций, т.к. они лучше интерпретируются и требуют меньшего объема наблюдений для оценки параметров.

Пример: рассчитаем показатель качества - коэффициент детерминации для уравнения:
f(xi)=18,67 + 5,68∙хi
R2=r2yx=0,9072=0,82.
То есть 82 % вариации объема продаж за период обусловлено влиянием фактора Х – численностью населения в торговой зоне. Соответственно, 18 % (100% - 82%) вариации объема продаж обусловлено влиянием прочих неучтенных факторов.
Если значение коэффициента детерминации существенно отличается от нуля, то уравнение регрессии можно признать качественным.

Прогнозирование по уравнению регрессии
означает построение доверительного интервала для ожидаемого (прогнозируемого) значения признака-результата Y при заданном значении признака-фактора Х (Xпрогноз).
Заранее задают уровень доверительной вероятности Рдов.
Доверительный интервал прогноза определяется так: (Yпрогноз – Δпрогноз; Yпрогноз + Δпрогноз),
где Yпрогноз – значение Y, полученное по уравнению регрессии: Yпрогноз =f(Xпрогноз);
Δпрогноз – предельная ошибка прогноза.
Δпрогноз= μпрогноза ∙ t,
где t – коэффициент доверия, определяемый по таблицам распределения Стьюдента, в зависимости от α=1-Рдов и числа степеней свободы=n-2.

μпрогноза – средняя ошибка прогноза определяется в случае линейной парной регрессии по формуле:
где s2u – средняя ошибка регрессии;
Хпрогн – значение признака фактора Х, для которого выполняется прогноз.
Средняя ошибка регрессии может быть определена по формуле:

Пример: требуется построитьдоверительный интервал для ожидаемого (прогнозируемого) значения Y, если Х примет значение равное 105% от своего среднего уровня. (Уровень доверительной вероятности Рдов взять равным 0,95).
Решение:
Хпрогнозное=1,05∙2,33=2,4465.
Yпрогнозное=18,67 + 5,68∙2,4465=32,56.
Для расчета предельной ошибки определим коэффициент доверия и среднюю ошибку прогноза.
t – коэффициент доверия, определяется по таблицам распределения Стьюдента. В нашем примере t (α=1-Рдов=0,05; число степеней свободы= n-2=20-2=18) = 2,1.