Содержание
- 2. Площадь криволинейной трапеции y x B C D A a b Y = f(x) s ABCD
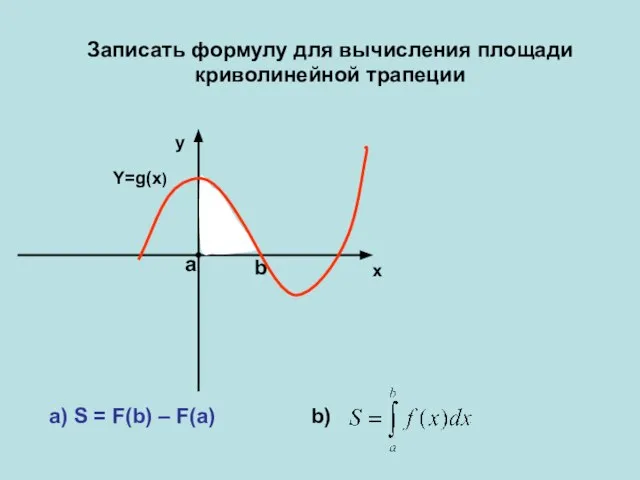
- 3. Y=g(x) x b a y Записать формулу для вычисления площади криволинейной трапеции а) S = F(b)
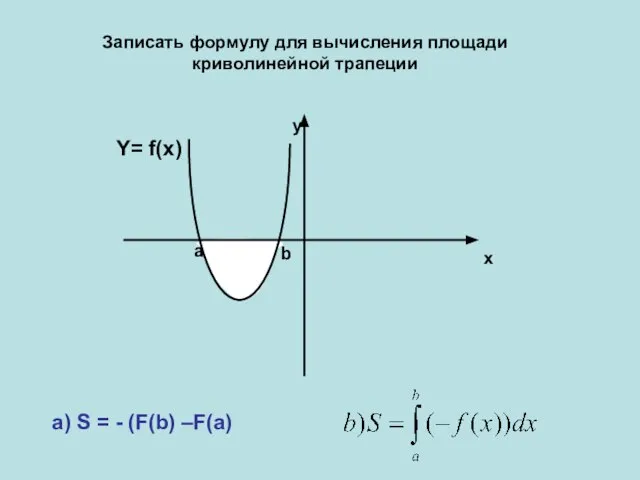
- 4. x y а b Y= f(x) a) S = - (F(b) –F(a) Записать формулу для вычисления
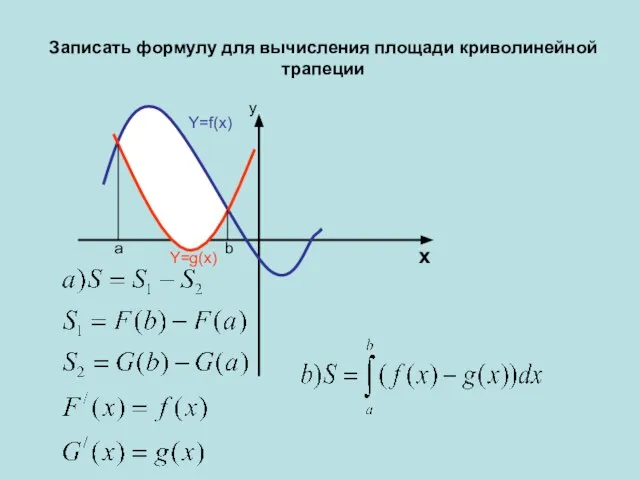
- 5. x a b y Y=f(x) Y=g(x) Записать формулу для вычисления площади криволинейной трапеции
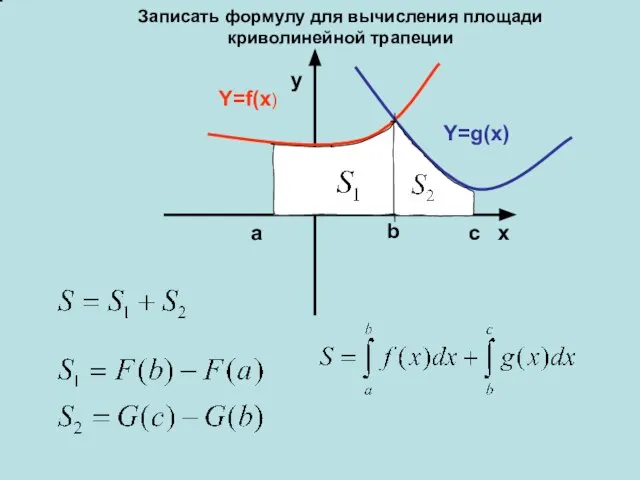
- 6. Y=f(x) Y=g(x) x y a b c Записать формулу для вычисления площади криволинейной трапеции
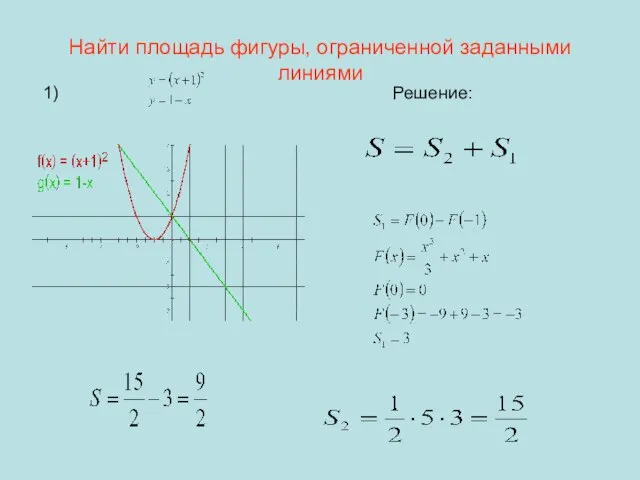
- 7. Найти площадь фигуры, ограниченной заданными линиями 1) Решение:
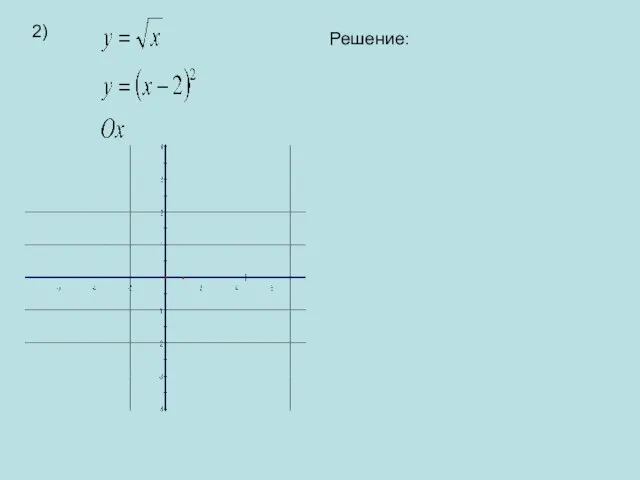
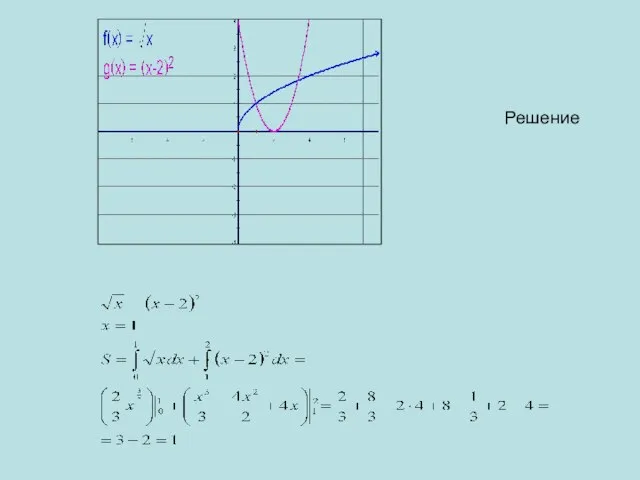
- 8. 2) Решение:
- 9. Решение
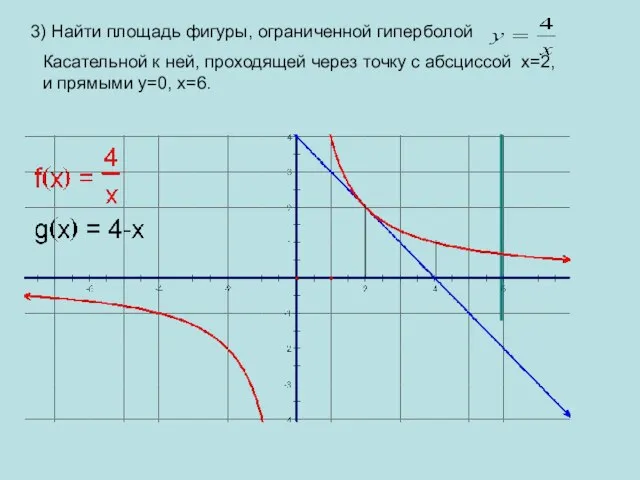
- 10. 3) Найти площадь фигуры, ограниченной гиперболой Касательной к ней, проходящей через точку с абсциссой х=2, и
- 11. способ:
- 12. 2 способ
- 13. 3 способ 1. 2.
- 14. 4) Используя геометрические соображения, вычислить интеграл:
- 15. Решение. а) Имеем: Это уравнение окружности радиуса r=2 с центром в точке (2;0). Значит, заданным интегралом
- 16. 5) Вычислить интеграл:
- 17. а) Фигура, площадь которой выражается заданным интегралом, состоит из сектора круга радиусом 2 и центральным углом
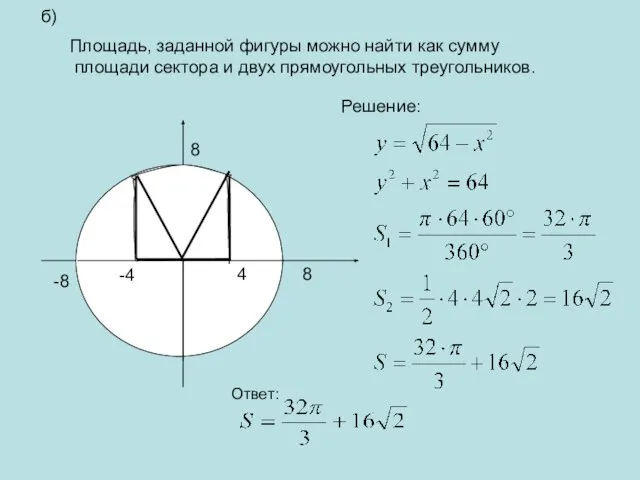
- 18. б) Площадь, заданной фигуры можно найти как сумму площади сектора и двух прямоугольных треугольников. Решение: Ответ:
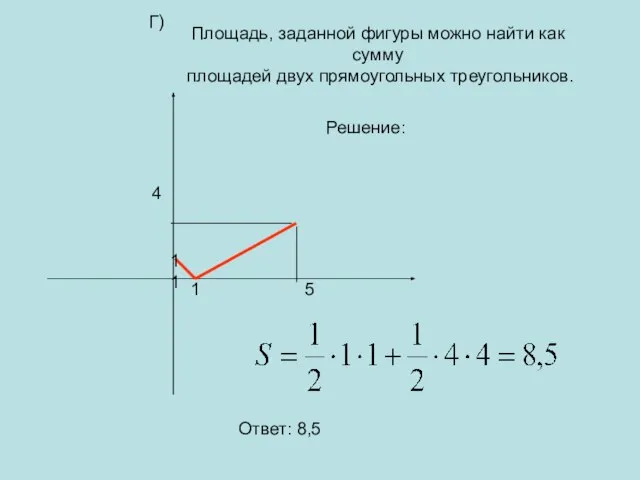
- 19. 11 Площадь, заданной фигуры можно найти как сумму площадей двух прямоугольных треугольников. Г) Решение: Ответ: 8,5
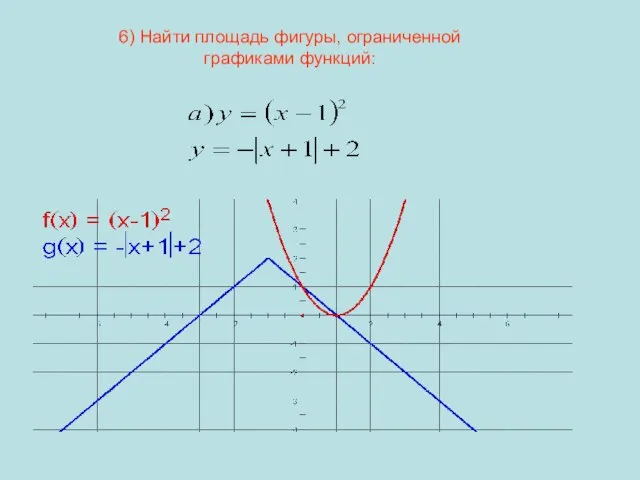
- 20. 6) Найти площадь фигуры, ограниченной графиками функций:
- 21. Решение: 7) Найти площадь фигуры, ограниченной графиком функции и касательной к нему в точке х=3 Заданная
- 23. Скачать презентацию

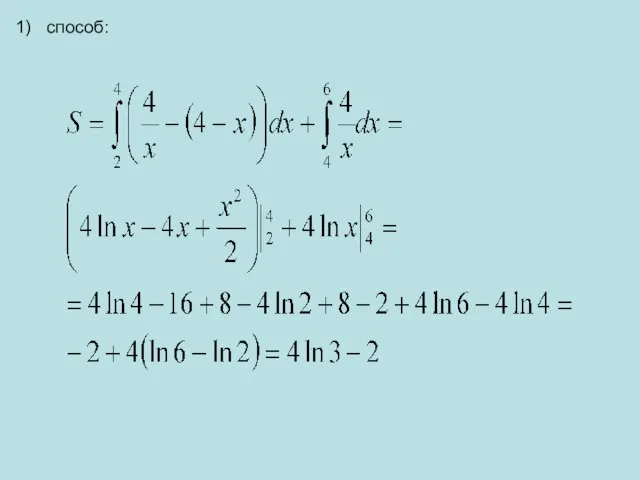
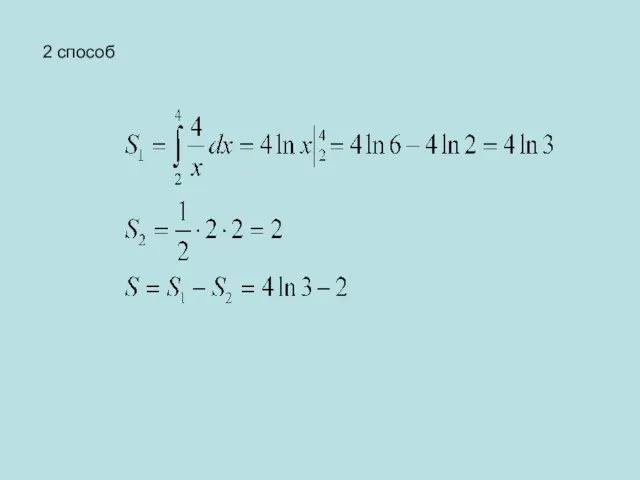
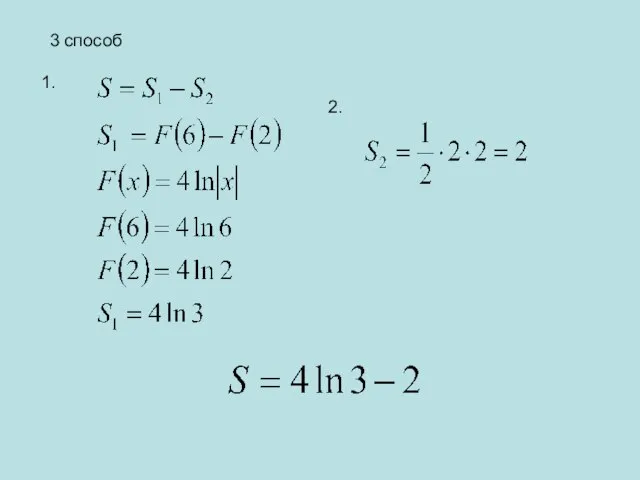


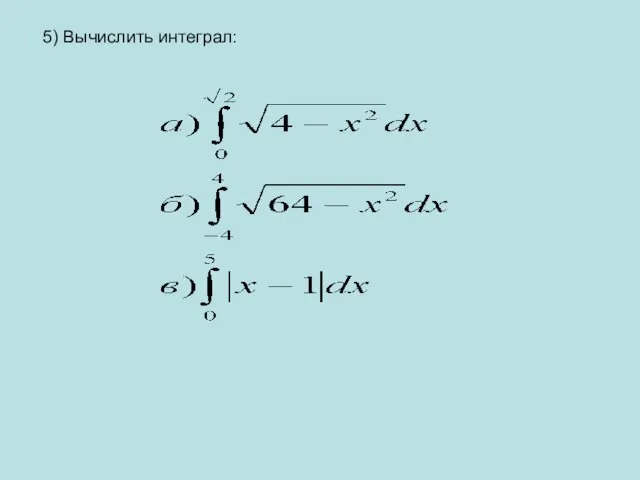


 Приемы вычислений для случаев вида 60-24
Приемы вычислений для случаев вида 60-24 Сравнение компьютерных технологий 90-х годов с последними разработками в этой сфере.
Сравнение компьютерных технологий 90-х годов с последними разработками в этой сфере. Самуил Яковлевич Маршак
Самуил Яковлевич Маршак Конструктивное построение предметов
Конструктивное построение предметов Patriot Burst Elite — бюджетное решение для любого пользователя ПК или ноутбука
Patriot Burst Elite — бюджетное решение для любого пользователя ПК или ноутбука Методика применения электронного учебного пособияпо базовому курсу информатики Руководитель проекта: Огарков А.Ю., учитель инфо
Методика применения электронного учебного пособияпо базовому курсу информатики Руководитель проекта: Огарков А.Ю., учитель инфо Петр Михайлович Врангель
Петр Михайлович Врангель Обществознание
Обществознание Форматирование текстового документа
Форматирование текстового документа Разработка малобюджетного учебного сайта на основе концепции Wiki
Разработка малобюджетного учебного сайта на основе концепции Wiki Спорт төрҙәре
Спорт төрҙәре Конкурс на лучшую модель школьной формы
Конкурс на лучшую модель школьной формы Кузнечик
Кузнечик Маркетинговая деятельность фирмы
Маркетинговая деятельность фирмы  WEB- браузеры
WEB- браузеры Занятие по лепке из пластилина в программе Картонный домик
Занятие по лепке из пластилина в программе Картонный домик Резонатор.Мск
Резонатор.Мск Головной мозг и его тайны!
Головной мозг и его тайны! Стратегия развития мариупольской городской организации
Стратегия развития мариупольской городской организации В гаванях афинского порта Пирей
В гаванях афинского порта Пирей Витамин C
Витамин C Красота и гармония
Красота и гармония Кластеры
Кластеры Технологические инновации SAPна службе вашего бизнеса
Технологические инновации SAPна службе вашего бизнеса Классный час «У истоков казачества» «казак» «вольный», «храбрый», «свободолюбивый человек», «удалой воин», «разбойник»
Классный час «У истоков казачества» «казак» «вольный», «храбрый», «свободолюбивый человек», «удалой воин», «разбойник» ИСТОРИЯ РАЗВИТИЯ МОУ ДОД «ЦЕНТР ДЕТСКОГО ТЕХНИЧЕСКОГО ТВОРЧЕСТВА» г. БЕЛГОРОДА
ИСТОРИЯ РАЗВИТИЯ МОУ ДОД «ЦЕНТР ДЕТСКОГО ТЕХНИЧЕСКОГО ТВОРЧЕСТВА» г. БЕЛГОРОДА Есть в осени первоначальной
Есть в осени первоначальной Крупнейшие библиотеки мира
Крупнейшие библиотеки мира