Слайд 2Под термином структура понимается совокупность устойчивых внутренних связей объекта, обеспечивающих его целостность

и тождественность самому себе, т.е. сохранение основных свойств при различных внешних и внутренних изменениях.
Слайд 3Статистическая структура – это распределение различных частей в пределах общего для них

качества, а также распределение составляющих совокупность единиц по количественному или качественному признаку
Слайд 4Классификация экономических структур
По фактору времени:
структуры моментные
структуры интервальные.

Слайд 5Моментные структуры характеризуют строение, состав финансово-экономических объектов или общие результаты финансово-экономических процессов

по состоянию на определенные моменты времени и отображаются посредством моментных относительных показателей (как правило, на начало или на конец периода).
Слайд 6Интервальные структуры характеризуют результаты финансово-экономических процессов или процессов формирования изучаемого объекта за

определенные периоды и отображаются интервальными относительными показателями. Наиболее часто в качестве рассматриваемых периодов используются годы, кварталы и месяцы, в то же время, в оперативном анализе рынка ценных бумаг применяются суточные и почасовые интервалы.
Слайд 7 Направления статистического исследования структуры:
1) анализ состава совокупности, вариации и распределения признаков;
2)

анализ динамики и прогнозирование отдельных структурных частей и совокупности в целом, т.е. структурных сдвигов;
3) анализ взаимосвязей структурных частей между собой и с другими объектами, выраженными как относительными, так и абсолютными показателями.
Слайд 8Показатели структуры позволяют измерить те количественные изменения, которым подвергалась каждая отдельно взятая

часть изучаемой совокупности
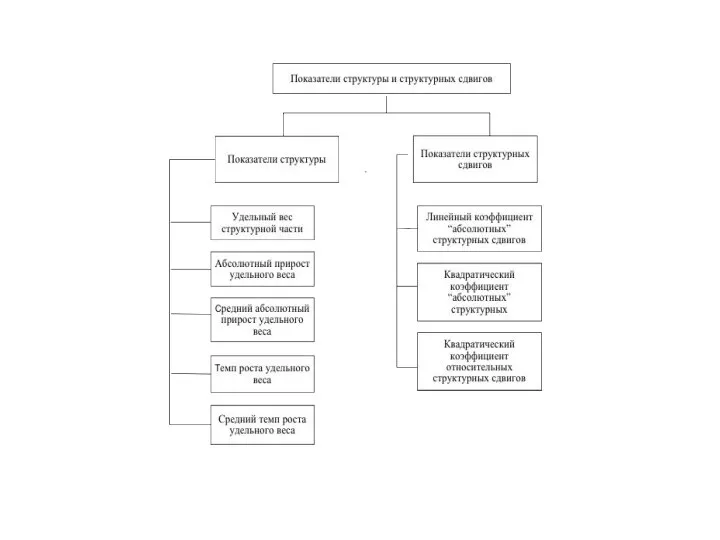
Слайд 9Показателей структуры и структурных сдвигов включает в себя показатели, которые позволяют получить

обобщающую оценку структурных изменениям во всей совокупности.
Слайд 11Цепные и средние показатели структурных сдвигов.
«Абсолютный» прирост удельного веса i-й части

совокупности позволяет определить, на какую величину в долях единицы или в процентах возросла или уменьшилась данная структурная часть в j-й период по сравнению с (j-1) периодом. Этот показатель рассчитывается по следующей формуле:
Где - удельный вес i-й части совокупности в (j-1)-й период.
Слайд 12 Темп роста удельного веса представляет собой отношение удельного веса i-й части

совокупности в j-й период времени к удельному весу этой же части в предшествующий период:
Слайд 132. Цепные и средние показатели структурных сдвигов.
Средний “абсолютный” прирост удельного веса

i-ой структурной части показывает, на сколько процентных пунктов в среднем за какой-либо период (день, неделю, месяц, год и т.п.) изменяется данная структурная часть:
где n - число осредняемых периодов.
Слайд 14 Средний темп роста удельного веса

Слайд 153. Определение средних удельных весов.
Исходные данные для определения удельных весов
(в

натуральном или стоимостном измерении)
Слайд 16 Средний удельный вес i-й структурной части:

Слайд 174. Обобщающие показатели структурных сдвигов.
Линейный коэффициент “абсолютных” структурных сдвигов:

Слайд 18Линейный коэффициент “абсолютных” структурных сдвигов, базируется на абсолютных значениях приростов удельных весов

отдельных частей совокупности в общем итоге и показывает среднее изменение удельного веса, которое имело место за рассматриваемый интервал времени.
Слайд 19 Квадратический коэффициент “абсолютных” структурных сдвигов:

Слайд 20Квадратический коэффициент “абсолютных” структурных, позволяет оценить интенсивность изменения удельных весов и показывает

средний относительный прирост удельного веса в изучаемом периоде.
Слайд 21 Линейный коэффициент относительных структурных сдвигов представляет собой среднюю арифметическую из абсолютных

значений отклонений темпов роста удельных весов от единицы, взвешенных по базисным удельным весам:
Слайд 22 Квадратический коэффициент относительных структурных сдвигов рассчитывается по формуле:

Слайд 23После преобразований данное выражение несколько упростится:
или

Слайд 24Квадратический коэффициент относительных структурных сдвигов позволяет получить сводную оценку интенсивности изменений удельных

весов и оценить средний относительный прирост удельного веса (в процентах), который наблюдался за рассматриваемый период.
Слайд 25 Приросты удельных весов совокупности X
за n периодов (%)
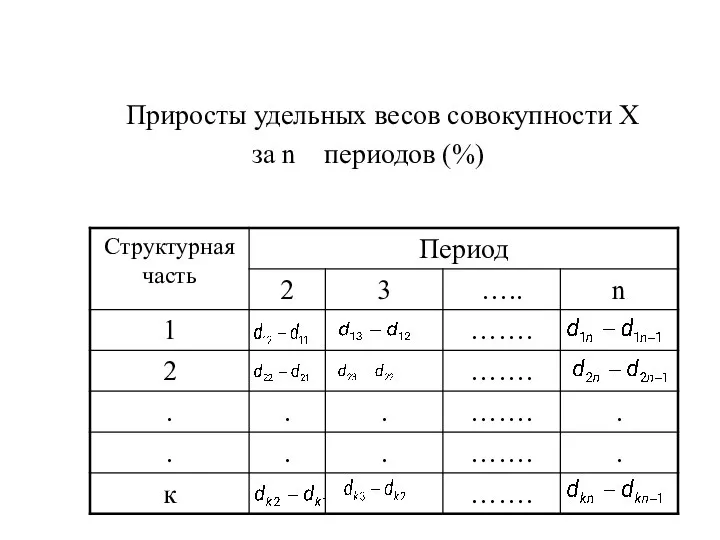
Слайд 26 Линейный коэффициент “абсолютных” структурных сдвигов за n периодов, учитывающий все промежуточные

структурные изменения, представляет собой сумму всех элементов матрицы приростов, взятых по модулю, деленную на количество этих элементов:
Слайд 27 Линейный коэффициент “абсолютных” структурных сдвигов за n периодов, ориентированный на конечные

результаты развития структуры, будет отличаться числителем, в котором суммируются общие приросты удельных весов всех групп за весь рассматриваемый период:
Слайд 28Для оценки значимости полученных результатов и существенности структурных сдвигов в изучаемых совокупностях

используют критерий χ2
Слайд 30Если расчетное значение больше критического, то структурные сдвиги в анализируемых структурах существенны.

Слайд 31Показатели концентрации
позволяют оценить, насколько равномерно объем изучаемого признака распределяется между всеми структурными

частями или между всеми единицами совокупности
Слайд 32Показатели концентрации
позволяют оценить, насколько равномерно объем изучаемого признака распределяется между всеми структурными

частями или между всеми единицами совокупности, или существует ли концентрация изучаемого явления у одной или нескольких структурных частей. С этой целью возможно рассчитать ряд показателей к которым относят
Слайд 335. Оценка уровня концентрации и централизации рынка ценных бумаг.
Общий вид кривой концентрации
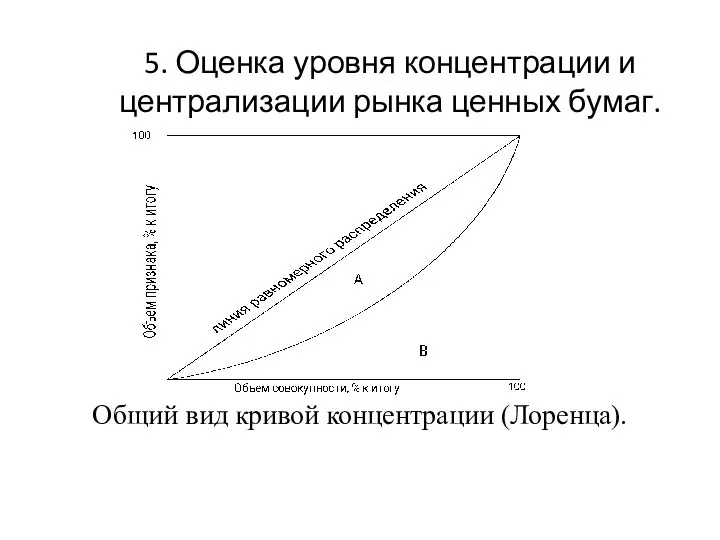
(Лоренца).
Слайд 35Коэффициент Джинни
Позволяет сравнивать распределение признака в совокупностях с различным числом единиц (например,

регионы с разным числом хозяйствующих субъектов).
Может быть использован для сравнения распределения признака между различными совокупностями (например, разными странами). При этом нет зависимости от масштаба экономики сравниваемых стран.
Может быть использован для сравнения распределения признака по разным группам населения (например, коэффициент Джини для финансового сектора и коэффициент Джини для нефте-газового комплекса).
Позволяет отслеживать динамику неравномерности распределения признака в совокупности на разных этапах.


























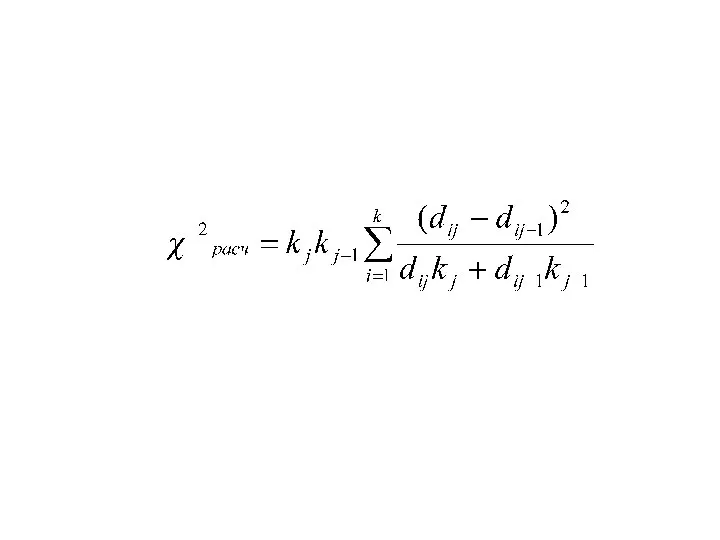






 Intermediate
Intermediate Урок рисования
Урок рисования М. Е. Салтыков-Щедрин «История одного города». Замысел, история создания, жанр и композиция романа
М. Е. Салтыков-Щедрин «История одного города». Замысел, история создания, жанр и композиция романа Художник и ученый (9 класс)
Художник и ученый (9 класс) Политика как призвание и профессия
Политика как призвание и профессия Презентация на тему А. Герасимова «После дождя»
Презентация на тему А. Герасимова «После дождя» Русская душа Донбасса
Русская душа Донбасса Передача жилых домов в управление
Передача жилых домов в управление Художественная культура Древней Греции
Художественная культура Древней Греции Прекращение и расторжение трудового договора
Прекращение и расторжение трудового договора Служебные части речи
Служебные части речи Графическое решение физических задач
Графическое решение физических задач Создание сети социальной поддержки выпускников интернатных учреждений в период профессиональной подготовки
Создание сети социальной поддержки выпускников интернатных учреждений в период профессиональной подготовки Во что верят люди? Религия. Тема №2
Во что верят люди? Религия. Тема №2 ВЫХОДИ В ИНТЕРНЕТ!
ВЫХОДИ В ИНТЕРНЕТ!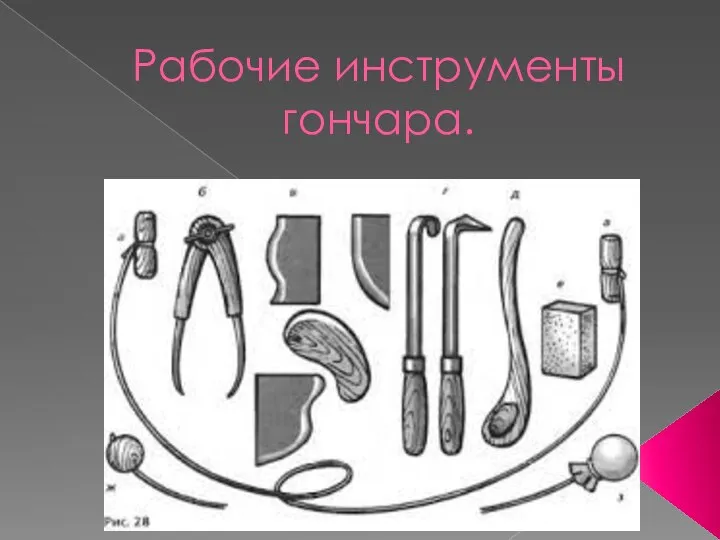 Рабочие инструменты гончара
Рабочие инструменты гончара Першагина Татьяна Юрьевна
Першагина Татьяна Юрьевна Художественные образы СПБ: российский город на перекрёстке мировых культур
Художественные образы СПБ: российский город на перекрёстке мировых культур Как стать богатым
Как стать богатым Ч Т О И З У Ч А Е Т
Ч Т О И З У Ч А Е Т Игры в eLearning
Игры в eLearning Презентация на тему Воды суши
Презентация на тему Воды суши порівняння чисел
порівняння чисел Представление о Power Point
Представление о Power Point Детские поделки на Пасху
Детские поделки на Пасху Муниципальной ресурсный центр «Система здоровьесберегающей деятельности в ОУ»
Муниципальной ресурсный центр «Система здоровьесберегающей деятельности в ОУ» Экологический кризис – глобальная проблема современности. На примере техногенных катастроф
Экологический кризис – глобальная проблема современности. На примере техногенных катастроф Молодёжь и политика
Молодёжь и политика