Свойства дефектов и их ансамблей в конденсированных средах

Содержание
Раздел 1 Виды отдельных элементарных дефектов и их свойства. Дефекты в простых веществах
1.1.Классификация дефектов простых веществ
1.1.1.Междоузлие
1.1.2.Вакансии в ковалентных соединениях
1.1.3. Характеристики точечных дефектов
1.1.4. Междоузлия в простых веществах и их характеристики
1.1.5. Дефекты упаковки
1.1.6. Неупорядоченные сплавы. Примесные дефекты
1.1.7. Упорядоченные сплавы. Типы решеток с упорядочением
1.2.Равновесные и неравновесные дефекты
1.2.1.Равновесная концентрация точечных дефектов в простых веществах
1.3. Дефекты упорядочивающихся сплавов
1.3.1.Метрика дальнего порядка в упорядочивающихся сплавах
1.3.2.Метрика ближнего порядка в упорядочивающихся сплавах. Связь дальнего порядка и среднего значения ближнего порядка в упорядочивающихся сплавах
1.3.3.Температурная зависимость концентрация равновесных дефектов замещения в упорядочивающихся сплавах
1.3.4. Температурная зависимость концентрация равновесных вакансий в упорядочивающихся сплавах

Содержание
Раздел 2. Описание дефектов кристаллической структуры в рамках теории упругости
2.1. Основные положения механики сплошной среды
2.1.1. Определения
2.1.2. Закон Гука
2.1.3. Закон Гука в обобщенном виде
2.1.4.Общий вид уравнений в абсолютных смещениях
2.2. Смещение атомов в кристаллической решетке с точечными дефектами. Изменение объема
2.3. Поведение дефекта во внешнем поле смещения
2.4. Плотность внутренних сил, эквивалентных центру дилатации
2.5. Взаимодействие дефектов с внешним упругим полем
2.6. Упругое взаимодействие точечных дефектов
2.7. Непрерывное распределение точечных дефектов в упругом поле
2.8. Течение кристалла. Ползучесть
2.9. Кинетика пор в кристалле
2.10. Неустойчивость однородного распределения точечных дефектов
2.11. Дислокации
2.12. Пластическая деформация кристаллов
2.13. Одномерная модель дислокации – модель Френкеля–Конторовой

Содержание
Раздел 3. Радиационные дефекты
3.1. Методы СОЗДАНИЯ РАДИАЦИОННЫХ ДЕФЕКТОВ
3.1.1. Облучение в реакторе
3.1.2. Облучение на ускорителях тяжелых ионов
3.1.3. Облучение в высоковольтном электронном микроскопе
3.1.4. Основные преимущества и недостатки экспрессивных методов радиационного испытания
3.2. Первичные процессы взаимодействия частиц и излучений с твердым телом
3.2.1. Общие представления о процессах взаимодействия частиц с твердым телом
3.2.2. Взаимодействие нейтронов с веществом
3.2.3. Взаимодействие ускоренных ионов с веществом
3.2.4. Распределение по глубине проникновения внедренных ионов и дефектов, созданных ионами
3.2.5. Взаимодействие электронов с веществом
3.2.6. Взаимодействие γ - квантов с веществом
3.3. Основные условия воспроизводимости явлений реакторного повреждения при облучении на ускорителе

Содержание
Раздел 4. Теоретическое сравнение структуры случайных полей радиационных дефектов, образующихся при облучении быстрыми частицами в пленочных образцах
4.1. Каскад атомных столкновений. Индивидуальные характеристики
4.2. Случайное поле дефектов. Статистика повреждений
4.3. Модель разреженных каскадов
4.4. Модель плотных каскадов
4.5. Параметры имитации
4.6. Имитационные соотношения для модельных спектров ПВА
4.7. Методика определения временного ресурса сверхпроводящих соединений
4.8. Расчет характеристик поля повреждений при облучении тонких пленок ионами и нейтронами со спектром, близким к реальному спектру ТЯР

Введение
«Физика реального твердого тела» изучает физические явления и процессы, обусловленные или возникающие при высоком содержании дефектов в твердом теле, пытается выработать предсказательные теории, определяющие характеристики твердого тела. Все области применения и «вынужденного» использования твердого тела, так или иначе, определяются дефектами структуры.
Простейшие примеры:
проводимость идеального твердого тела равна нулю;
критический ток в сверхпроводниках также равен нулю в отсутствии пиннинга системы вихрей на дефектах структуры.
Важным направлением является контролируемое введение в матрицу примесей и дефектов, а также радиационно-стимулированное изменение структуры. Начало интенсивного развития этого направления соответствует появлению полупроводниковых приборов. Это направление можно назвать «Физической технологией» поскольку конструирование и создание новых приборов и инструментария исследователей определяется разработкой детальной физической картины процессов, интерпретации измеряемых величин. Естественное уменьшение размеров изучаемых объектов и новые измерительные возможности привели к появлению нового направления «Наносистемы».
Контролируемое введение в матрицу примесей и дефектов представляет и физический интерес для анализа применимости тех или иных представлений физики конденсированных сред. Например, для анализа механизма сверхпроводимости в соединениях со структурой А15, ВТСП.

Ряд проблемных задач физики конденсированных систем имеет фундаментальный характер
Предсказание механических свойств реальных твердых тел, в том числе в интенсивных радиационных полях;
Электрические свойства и явления в конденсированных системах с высоким содержанием дефектов;
Механизмы сверхпроводимости, в том числе – высокотемпературной, улучшение критических параметров сверхпроводников;
Электронные и фотонные свойства органических полупроводников и кристаллов

ВИДЫ ОТДЕЛЬНЫХ ЭЛЕМЕНТАРНЫХ ДЕФЕКТОВ И ИХ СВОЙСТВА.
ДЕФЕКТЫ В ПРОСТЫХ ВЕЩЕСТВАХ.

Классификация дефектов простых веществ.
Определение: Любые нарушения или искажения в регулярности расположения атомов кристалла считают дефектом кристаллической решетки.
Различают следующие виды отдельных дефектов:
Тепловое движение атомов
Междоузельные атомы и вакансии
Примесные атомы
Граница кристалла
Поликристаллы
Дислокации
Статические смещения решетки вблизи дефекта

1.Тепловое движение атомов
отклонение атомов от положения равновесия;
это термодинамически-равновесный вид дефекта, имеющий динамический характер.

2.Междоузельные атомы и вакансии.
Эти дефекты имеют тенденцию быть равновесными.
Характерное время релаксации к равновесному состоянию может быть достаточно большим.
Действительно, процесс диффузии дефектов, определяющий их распределение в твердом теле, является термоактивируемым процессом, поэтому при недостаточно больших температурах часто встречаются неравновесные состояния систем этих дефектов .
Значительным отличием систем точечных дефектов является наличие их взаимодействия между собой (через атомы матрицы), что приводит, в частности, к образованию их комплексов (ансамблей), конденсата в матрице, т.е. равновесное состояние системы точечных дефектов в большинстве случаев является неоднородным в пространстве (например, вакансии - ансамбль вакансий – пора).

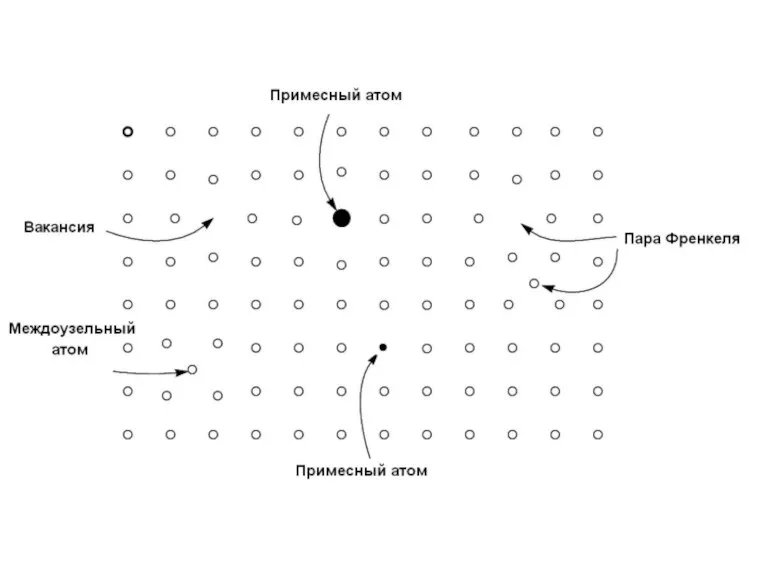
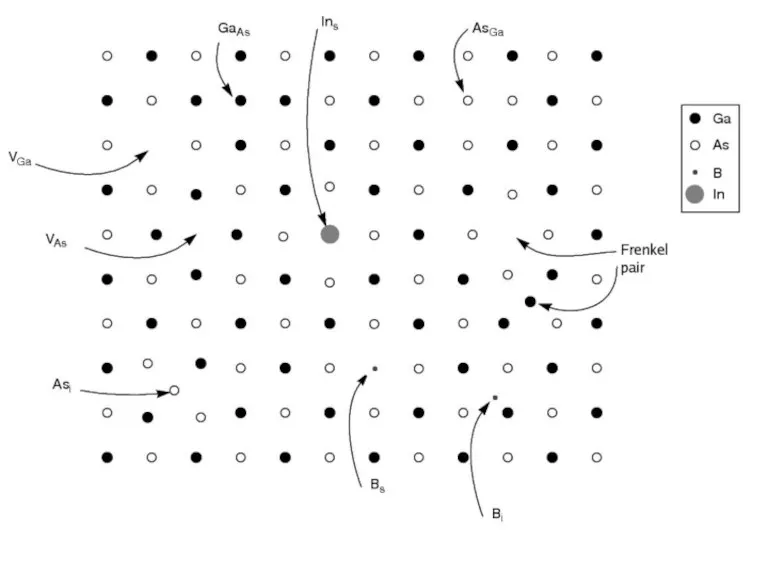
3. Атомы примесей
Примеси, даже при малой концентрации, могут существенно влиять на свойства кристалла, например, они вносят заметный вклад в проводимость полупроводников
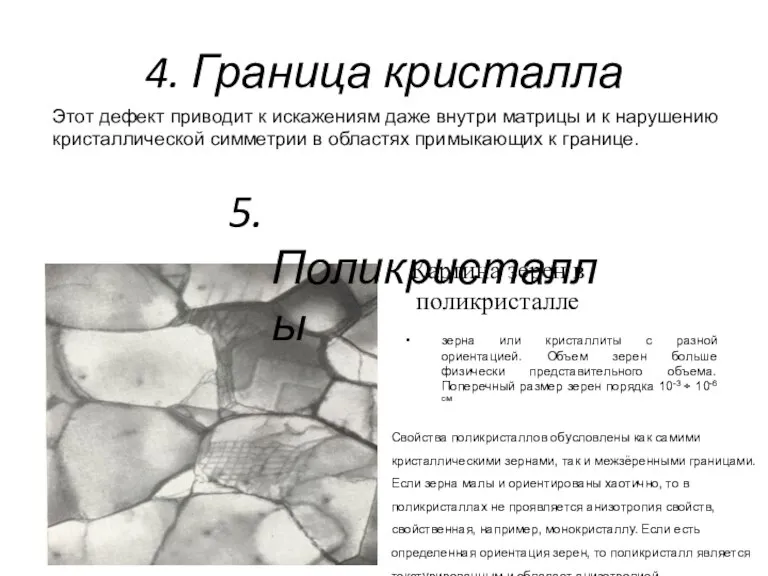
Плотность атомов в конденсированных системах 1022 - 1023 атомов/см3, концентрация дефектов в зависимости от предыстории получения образца меняется от 1012 - 1020 атом/см3.

4. Граница кристалла
Этот дефект приводит к искажениям даже внутри матрицы и к нарушению кристаллической симметрии в областях примыкающих к границе.
Картина зерен в поликристалле
5. Поликристаллы
зерна или кристаллиты с разной ориентацией. Объем зерен больше физически представительного объема. Поперечный размер зерен порядка 10-3 ÷ 10-6 см
Свойства поликристаллов обусловлены как самими кристаллическими зернами, так и межзёренными границами. Если зерна малы и ориентированы хаотично, то в поликристаллах не проявляется анизотропия свойств, свойственная, например, монокристаллу. Если есть определенная ориентация зерен, то поликристалл является текстурированным и обладает анизотропией.

Выход краевой
дислокации на границу
Винтовая дислокация роста кристалла.
Скопление дислокаций на межзеренных границах
Сетка дислокаций
Винтовая дислокация
5. Дислокации – неравновесный тип дефекта, т.е. их появление обусловлено предысторией образца и связано либо ростом кристаллита, либо действием внешних нагрузок или воздействий.
Различают несколько типов дислокаций: краевые, винтовые, смешанные. Их скопления часто формируют межзеренные границы.

В зависимости от размерности различают следующие типы дефектов:
1. Точечные дефекты: Междоузельные атомы и вакансии, Примесные атомы
2. Линейные дефекты :Дислокации
3. Плоские дефекты: Граница кристалла, Поликристаллы
Феноменологические характеристики точечных дефектов:
- энергия образования;
- энергия миграции;
- дилатационный объём.

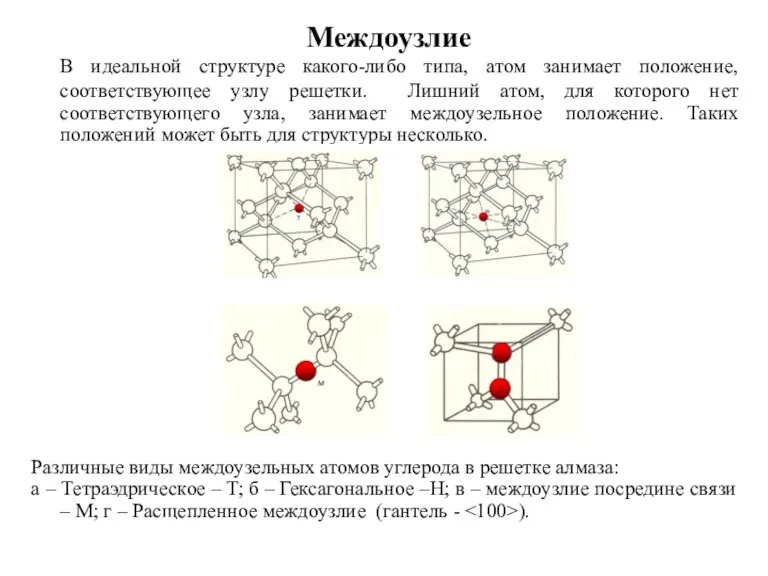
В идеальной структуре какого-либо типа, атом занимает положение, соответствующее узлу решетки. Лишний атом, для которого нет соответствующего узла, занимает междоузельное положение. Таких положений может быть для структуры несколько.
Различные виды междоузельных атомов углерода в решетке алмаза:
а – Тетраэдрическое – T; б – Гексагональное –H; в – междоузлие посредине связи – M; г – Расщепленное междоузлие (гантель - <100>).
Междоузлие

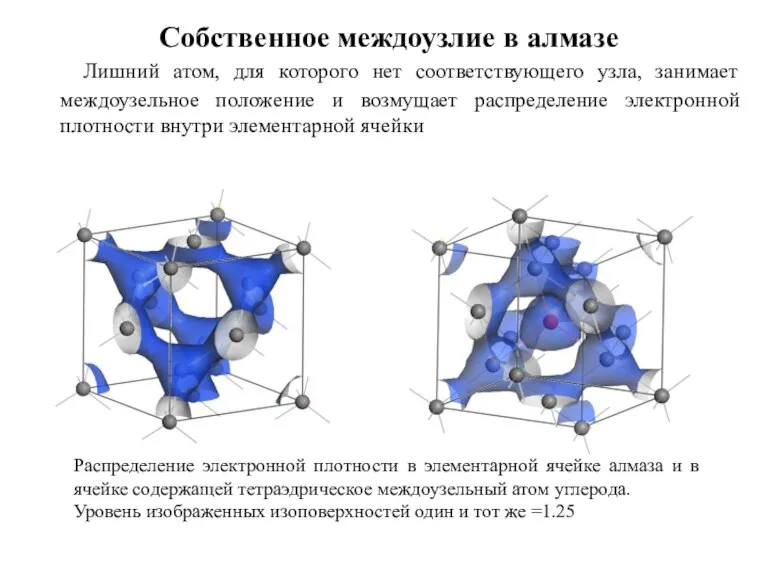
Лишний атом, для которого нет соответствующего узла, занимает междоузельное положение и возмущает распределение электронной плотности внутри элементарной ячейки
Собственное междоузлие в алмазе
Распределение электронной плотности в элементарной ячейке алмаза и в ячейке содержащей тетраэдрическое междоузельный атом углерода.
Уровень изображенных изоповерхностей один и тот же =1.25

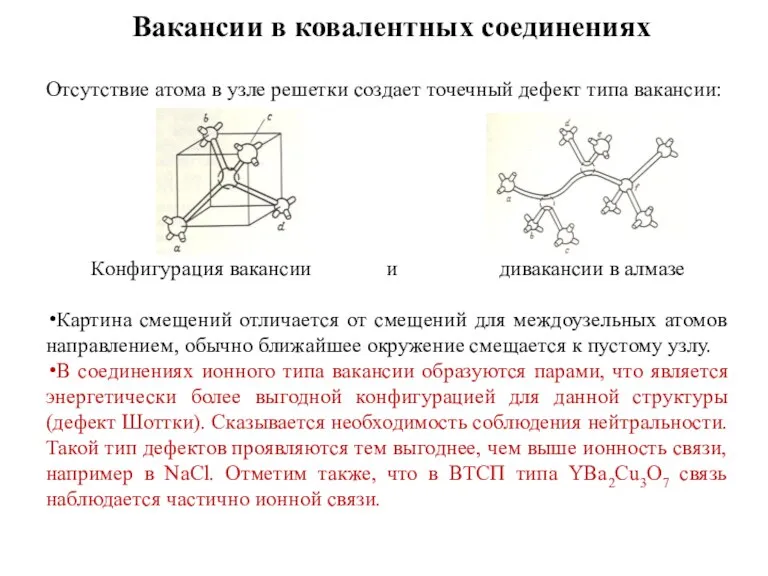
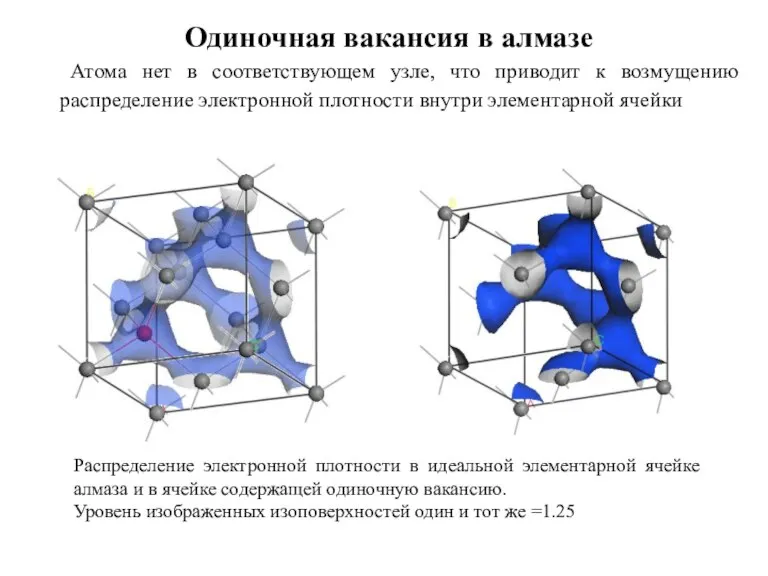
Вакансии в ковалентных соединениях
Отсутствие атома в узле решетки создает точечный дефект типа вакансии:
Конфигурация вакансии и дивакансии в алмазе
Картина смещений отличается от смещений для междоузельных атомов направлением, обычно ближайшее окружение смещается к пустому узлу.
В соединениях ионного типа вакансии образуются парами, что является энергетически более выгодной конфигурацией для данной структуры (дефект Шоттки). Сказывается необходимость соблюдения нейтральности. Такой тип дефектов проявляются тем выгоднее, чем выше ионность связи, например в NaCl. Отметим также, что в ВТСП типа YBa2Cu3O7 связь наблюдается частично ионной связи.

Атома нет в соответствующем узле, что приводит к возмущению распределение электронной плотности внутри элементарной ячейки
Одиночная вакансия в алмазе
Распределение электронной плотности в идеальной элементарной ячейке алмаза и в ячейке содержащей одиночную вакансию.
Уровень изображенных изоповерхностей один и тот же =1.25

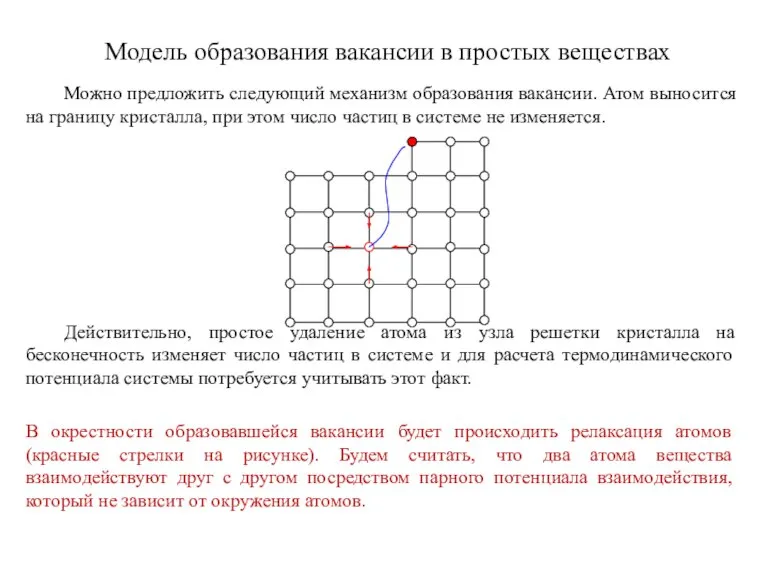
Модель образования вакансии в простых веществах
Можно предложить следующий механизм образования вакансии. Атом выносится на границу кристалла, при этом число частиц в системе не изменяется.
Действительно, простое удаление атома из узла решетки кристалла на бесконечность изменяет число частиц в системе и для расчета термодинамического потенциала системы потребуется учитывать этот факт.
В окрестности образовавшейся вакансии будет происходить релаксация атомов (красные стрелки на рисунке). Будем считать, что два атома вещества взаимодействуют друг с другом посредством парного потенциала взаимодействия, который не зависит от окружения атомов.

Энергия атома, находящегося в узле кристалла, равна Eузл=z1*φ(R*), где число ближайших соседей порядка z1 ≈ 6 - 8, R*– равновесное межатомное расстояние, оценка потенциала φ(R*) может быть сделана, например, из энергии сублимации вещества, что дает φ(R*) ≈ 0.2 ÷ 0.3eV. Таким образом, величина энергии атома в узле решетки равна Eузл~ 1.6 ÷ 2.4 эВ. Такая энергия должна быть затрачена на разрыв связей при образовании вакансии. Однако вынутый атом размещается на поверхности, следовательно, можно считать, что половина разорванных связей восстанавливается. Энергия атома, находящегося на поверхности равна. Таким образом, величина энергия формирования вакансии Ef ≈ 0.8 ÷ 1.2 эВ.
Миграция ваканисии
Рассмотрим миграцию вакансий. Чтобы атом А перепрыгнул на пустой узел, в котором расположена вакансия, казалось бы ему не нужно преодолевать барьер, но это не так – надо разорвать связи.
Расчет энергии формирования вакансии

Кроме того, вдоль траектории миграции вакансии (или атома А) возникает энергетический барьер (энергетическая линза), создаваемый ближайшими атомами. Это наиболее наглядно видно в трехмерном кристалле
Число ближайших соседей в сечении ABCD обычно меньше, чем у узле, z2 = 4. Если предположить, что парный потенциал меняется слабо, то величину энергетического барьера для миграции вакансии можно оценить Emγ ≈ 0.8 ÷ 1 эВ.

Дилатационный объем вакансии
Пусть ω0 – объем, приходящийся на один атом твердого тела. При образовании вакансии поверхность за счет релаксации исказится, и объем кристалла V изменится. Оценки дают примерно δV(1)= - 0.1ω0, это результат был получен на основании результатов дилатационных экспериментов, связанных с введением в образец множества вакансий. Отметим, что в матрице окружающей область образования вакансии происходит некоторое увеличение плотности вещества за счет релаксации.
В рассмотренном выше механизме образовании вакансии атом выходит на поверхность. Связанное с этим дополнительное изменение объема составляет δV(2)=+ω0. Таким образом, суммарное изменение объема кристалла равно:
δV=δV(1) + δV(2) =+0.9ω0
Изменение объема

Междоузлия в простых веществах и их характеристики
Рассмотрим следующий механизм формирования междоузельного атома. Пусть при формировании междоузлия атом вносится в кристалл с поверхности.
Оценка энергии дает величину zi∙φ(R), где zi - число ближайших соседей, R – расстояние минимального сближения междоузельного атома с ближайшими соседями. При этом, R < R* - равновесного расстояния в решетке, т.е. потенциальная энергия парного взаимодействия больше. Положение равновесия междоузельного атома определяется равновесием сил всех взаимодействующих пар. Число соседей определяется типом междоузлий. Как показывает эксперимент, обычно для наиболее представительного типа междоузлий энергия образования составляет величину Efi~ 3 ÷ 5 эВ и больше, чем для вакансий .
В отличие от вакансии у междоузельного атома могут быть разные стационарные положения в одной решетке с разными энергиями образования -это означает, что в равновесии заселенность этих состояний будет различной. Если , то при низких температурах – заселены междоузлия типа 1. При повышении температуры – заселяются и места 2. В радиационных процессах междоузельные дефекты второго типа могут рождаться и при низких температурах.

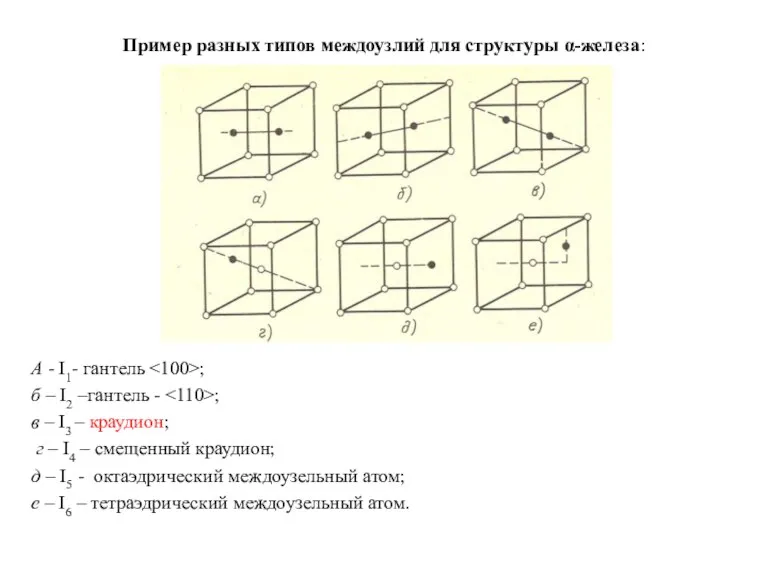
Пример разных типов междоузлий для структуры α-железа:
А - I1- гантель <100>;
б – I2 –гантель - <110>;
в – I3 – краудион;
г – I4 – смещенный краудион;
д – I5 - октаэдрический междоузельный атом;
е – I6 – тетраэдрический междоузельный атом.

Величина энергия миграции междоузлия оценивается как EmI ~ 0.1 эВ, т.е. EmI << EmV - энергии миграции вакансий. Этот факт обусловлен тем, что, как следует из численных расчетов характерное расстояние равновесия до ближайших соседей для междоузельного атома порядка тех расстояний, на которых междоузельный атом преодолевает энергетический барьер при прохождении линзы.
Число же ближайших соседей zI ≈ zL,т.е. высота барьера для миграции междоузельного атома должна быть мала.
Рассмотрим вопрос о дилатационном объеме междоузлия. Как показывают дилатационные эксперименты при образовании междоузельного дефекта происходит увеличение объема кристалла. Величина изменения объема, приходящаяся на один междоузельный атом δV(1)=+0.1ω0. При образовании междоузлия твердое тело немного «распухает».
Как и в случае с вакансией, при образовании
междоузельного атома в матрице и соответственно
его исчезновением на поверхности, дополнительное
изменение объема образца составляет δV(2)= - ω0.
Таким образом, суммарное изменение объема
кристалла равно δV=δV(1) + δV(2) = - 0.9ω0

Разница между дилатационными и дифракционными измерениями!

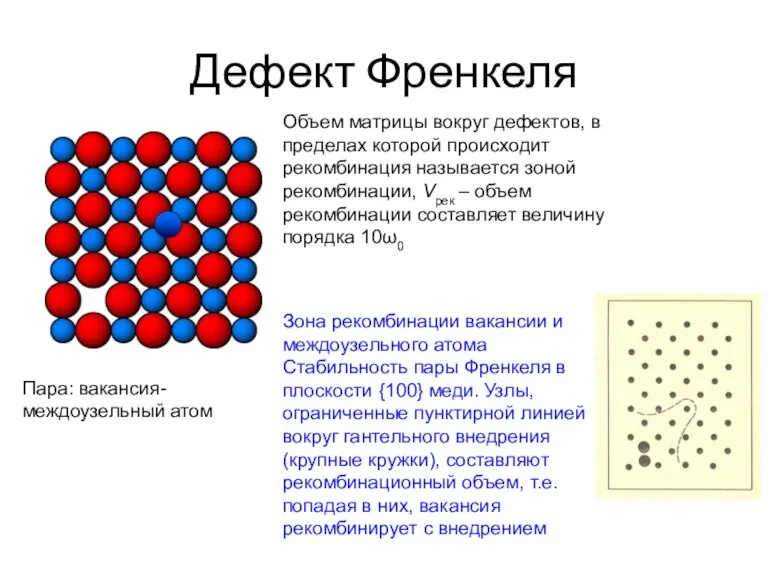
Дефект Френкеля
Пара: вакансия-междоузельный атом
Объем матрицы вокруг дефектов, в пределах которой происходит рекомбинация называется зоной рекомбинации, Vрек – объем рекомбинации составляет величину порядка 10ω0
Зона рекомбинации вакансии и междоузельного атома Стабильность пары Френкеля в плоскости {100} меди. Узлы, ограниченные пунктирной линией вокруг гантельного внедрения (крупные кружки), составляют рекомбинационный объем, т.е. попадая в них, вакансия рекомбинирует с внедрением

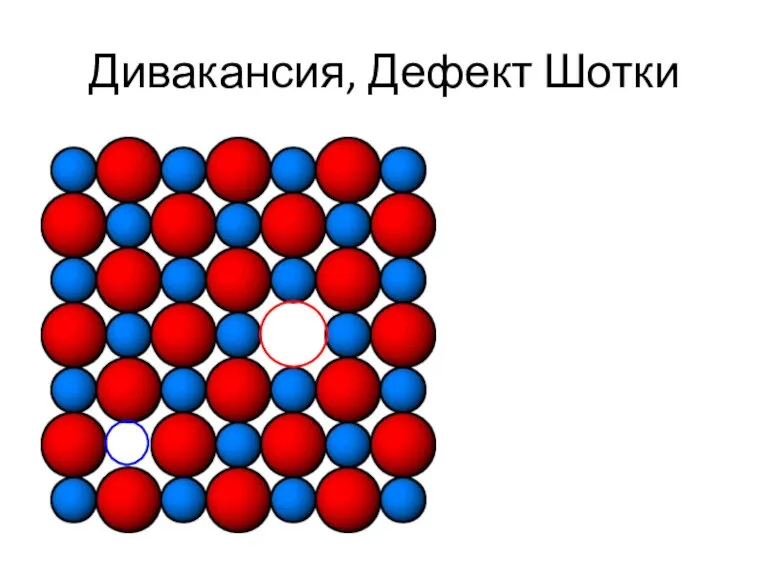
Дивакансия, Дефект Шотки