Содержание
- 2. Что такое периметр? Сформулируйте 1 признак равенства треугольников. ?
- 3. Повторение: Какой отрезок называется медианой? сколько медиан имеет треугольник? ?
- 4. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника
- 5. Какой отрезок называется биссектрисой? Сколько биссектрис имеет треугольник? Какой отрезок называется биссектрисой? Сколько биссектрис имеет треугольник?
- 6. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника
- 7. Какой отрезок называется высотой? Сколько высот имеет треугольник? Какой отрезок называется высотой? Сколько высот имеет треугольник?
- 8. Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника
- 9. Треугольник, две все стороны которого равны, называется равнобедренным основание Боковая сторона Боковая сторона
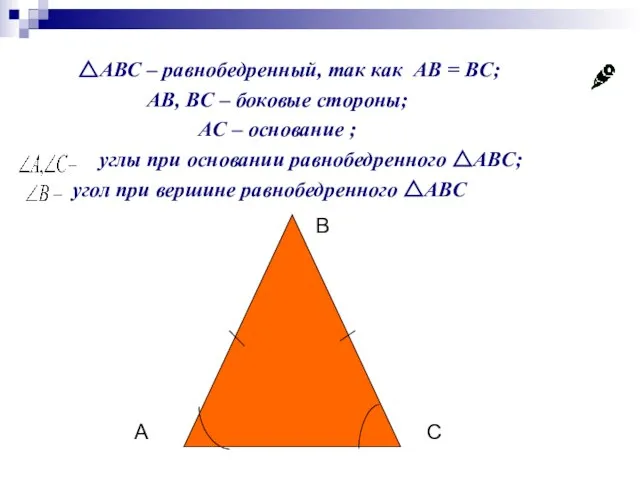
- 10. △ABC – равнобедренный, так как AB = BC; AB, BC – боковые стороны; AС – основание
- 11. Треугольник, все стороны которого равны, называется равносторонним
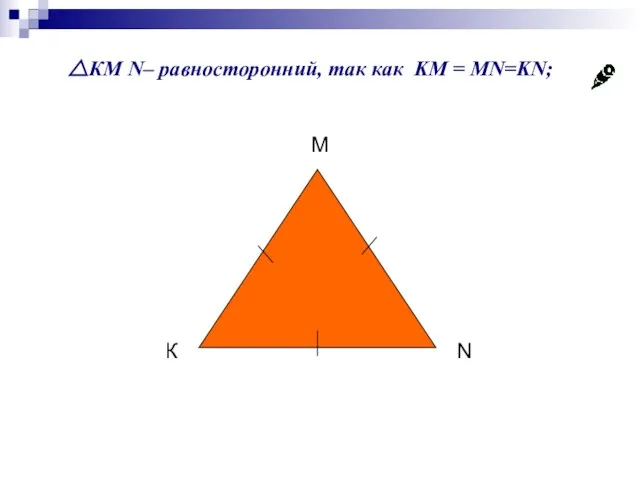
- 12. △КМ N– равносторонний, так как KM = MN=KN; К М N
- 13. «Свойства равнобедренного треугольника» Практическая работа
- 14. В равнобедренном треугольнике углы при основании равны Теорема: 1 СВОЙСТВО РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА
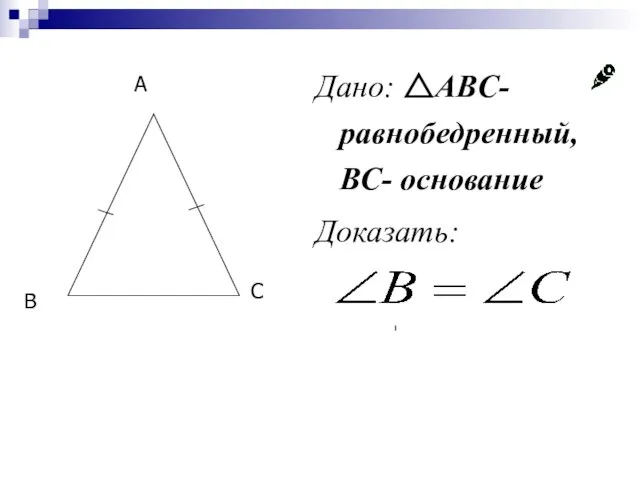
- 15. Дано: △ABC-равнобедренный, ВС- основание Доказать: B C A
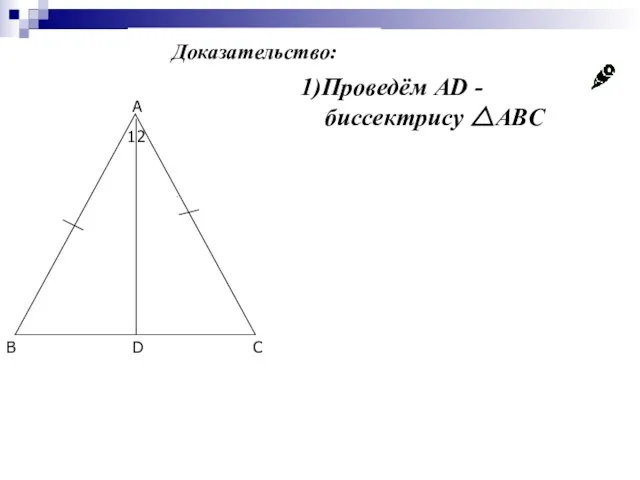
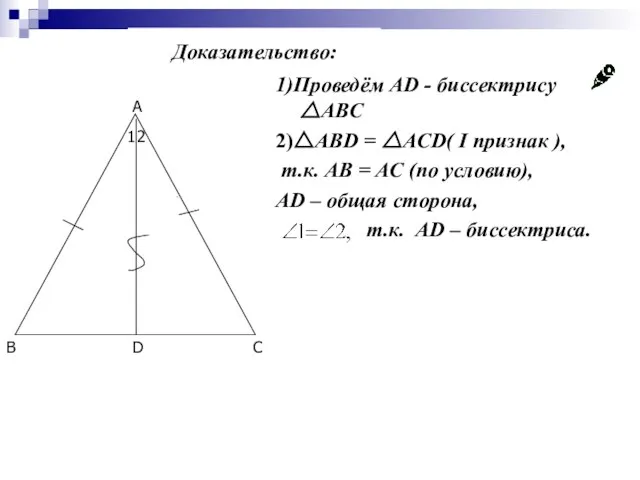
- 16. 1)Проведём AD - биссектрису △ABC Доказательство:
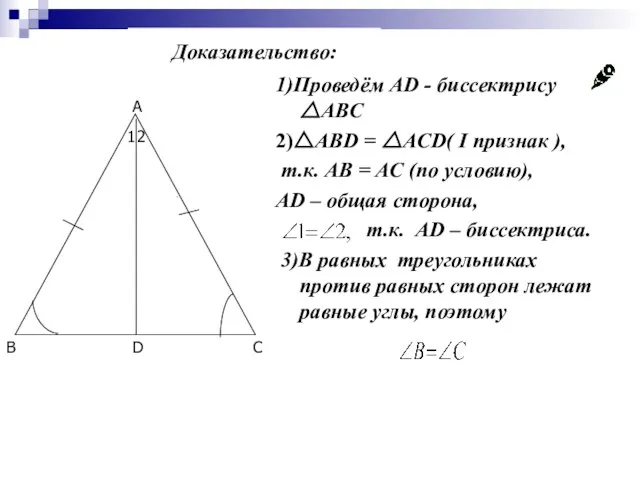
- 17. 1)Проведём AD - биссектрису △ABC 2)△ABD = △ACD( I признак ), т.к. AB = AC (по
- 18. 1)Проведём AD - биссектрису △ABC 2)△ABD = △ACD( I признак ), т.к. AB = AC (по
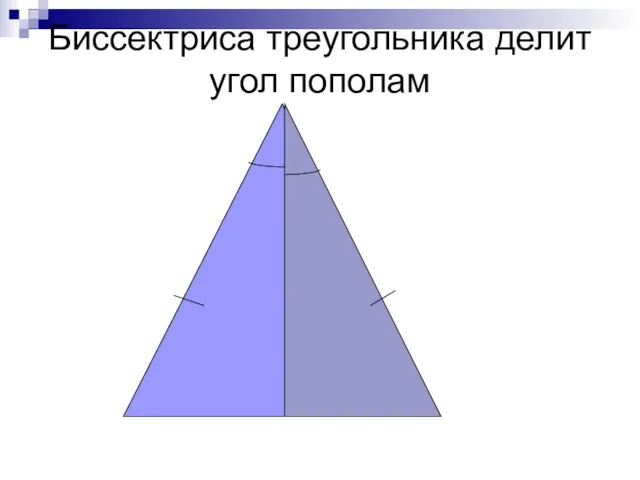
- 19. Биссектриса треугольника делит угол пополам
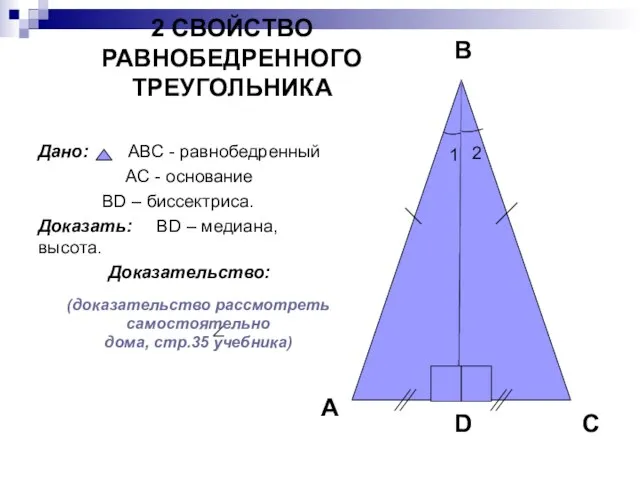
- 20. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой Теорема: 2 СВОЙСТВО РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА
- 21. 2 СВОЙСТВО РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА Дано: АВС - равнобедренный АС - основание ВD – биссектриса. Доказать: ВD
- 22. Самостоятельная работа Вариант I Исследуйте медианы равнобедренного треугольника и перечислите все их особенности и свойства. Вариант
- 23. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой Высота равнобедренного треугольника, проведенная к основанию,
- 24. Равнобедренные и равносторонние треугольники в жизни
- 25. КРЫШИ ДОМОВ И БАШЕН
- 26. ПАКЕТ С МОЛОКОМ
- 27. ЕГИПЕТСКИЕ ПИРАМИДЫ
- 28. СЕВЕРНЫЕ РОСПИСИ
- 29. ПАБЛО ПИКАССО «ВИНСЕНТ ВАН ГОГ»
- 30. Домашнее задание: § 18, вопросы 10-13 (стр. 50) № 108, № 112 Привести пример применения равнобедренных
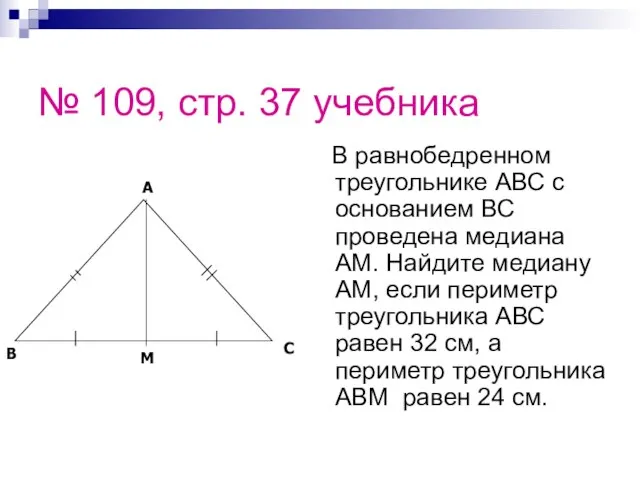
- 31. № 109, стр. 37 учебника В равнобедренном треугольнике АВС с основанием ВС проведена медиана АМ. Найдите
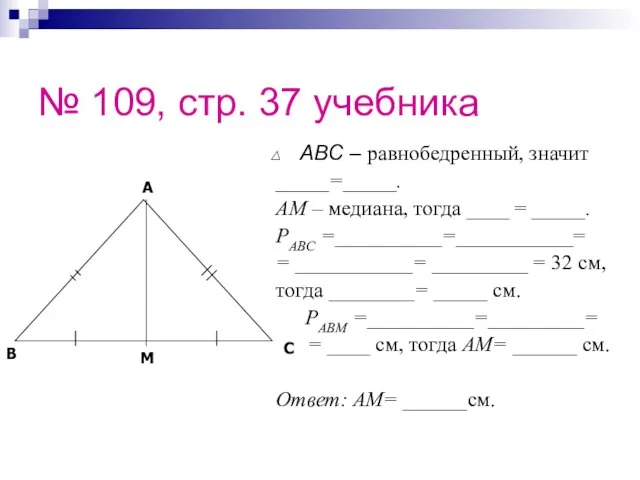
- 32. № 109, стр. 37 учебника ABC – равнобедренный, значит _____=_____. AM – медиана, тогда ____ =
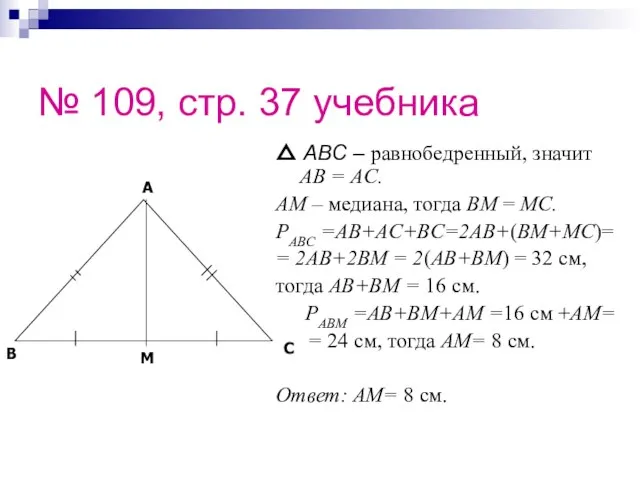
- 33. № 109, стр. 37 учебника △ ABC – равнобедренный, значит AB = AC. AM – медиана,
- 34. Тест «Свойства равнобедренного треугольника»
- 35. Тест «Свойства равнобедренного треугольника»
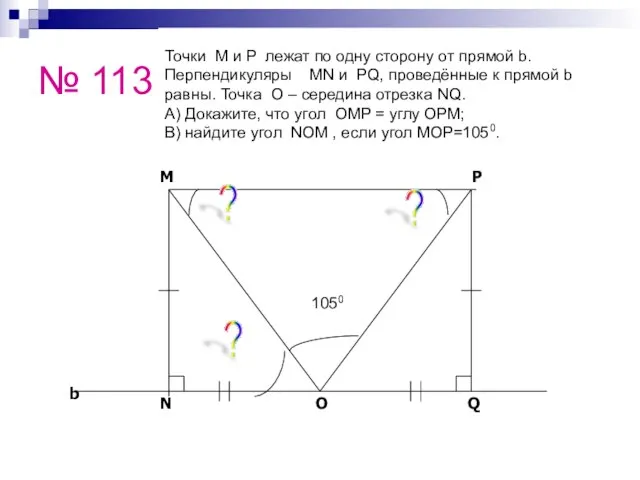
- 36. № 113 Точки M и P лежат по одну сторону от прямой b. Перпендикуляры MN и
- 37. №107 Самостоятельно
- 39. Скачать презентацию
























 Абхазский язык
Абхазский язык Свободная дислокация по билбордам г. Астана (ноябрь)
Свободная дислокация по билбордам г. Астана (ноябрь) Ломоносов Михаил Васильевич 19 ноября 1711г. – 15 апреля 1765 г
Ломоносов Михаил Васильевич 19 ноября 1711г. – 15 апреля 1765 г А. П. Чехов«Ионыч»Духовная деградация человекаЦуркан Алла Владимировнаучитель русского языка и литературыООШ № 20 г. Одессы
А. П. Чехов«Ионыч»Духовная деградация человекаЦуркан Алла Владимировнаучитель русского языка и литературыООШ № 20 г. Одессы Кадастровая палата Костромской области. Получение сертификата электронной подписи
Кадастровая палата Костромской области. Получение сертификата электронной подписи ТЕСТ - универсальный
ТЕСТ - универсальный Животные в психоисследованиях
Животные в психоисследованиях Презентация на тему Волшебные голоса
Презентация на тему Волшебные голоса  Plastic Surgery
Plastic Surgery  Периферийное устройство для обеспечения передвижения пользователя и взаимодействия с объектами в виртуальной реальности
Периферийное устройство для обеспечения передвижения пользователя и взаимодействия с объектами в виртуальной реальности Can you tell me the way to the zoo, please
Can you tell me the way to the zoo, please Информационно-графические системы моделирования режимов централизованного теплоснабжения
Информационно-графические системы моделирования режимов централизованного теплоснабжения Образ Снегурочки
Образ Снегурочки Проект детского образовательного центра или др образовательного учреждения
Проект детского образовательного центра или др образовательного учреждения «Создание среды электронного обучения «1 ученик: 1 компьютер»
«Создание среды электронного обучения «1 ученик: 1 компьютер» Его величество театр
Его величество театр Организация исследовательской работы в начальной школе
Организация исследовательской работы в начальной школе Проект команды Black Box
Проект команды Black Box Налог на имущество организации
Налог на имущество организации Поэма А.С. Пушкина «Полтава» (7 класс)
Поэма А.С. Пушкина «Полтава» (7 класс) Памятники религиозной культуры в моем селе
Памятники религиозной культуры в моем селе Raspiska
Raspiska The “ALMATY RESIDENCE” Business Centre & Apart Hotel: a classical Tuscan manner adaptation / ppt-Presentation by Dr. Konstantin I.Samoilov. - Almaty, 2016. – 46 p.
The “ALMATY RESIDENCE” Business Centre & Apart Hotel: a classical Tuscan manner adaptation / ppt-Presentation by Dr. Konstantin I.Samoilov. - Almaty, 2016. – 46 p. e30c1d9ff820ff9c7f35d061f4cbd83a
e30c1d9ff820ff9c7f35d061f4cbd83a Back to School
Back to School Применение информационных технологий в отраслях, на производстве и в жизни
Применение информационных технологий в отраслях, на производстве и в жизни Истина где-то рядом
Истина где-то рядом Подготовила учитель математики МОУ СОШ №36 г. Калининграда Ковальчук Лариса Леонидовна
Подготовила учитель математики МОУ СОШ №36 г. Калининграда Ковальчук Лариса Леонидовна