Содержание
- 2. Схема исследования: Область определения Множество значений Нули функции Интервалы знакопостоянства Промежутки монотонности Точки экстремума Набольшее и
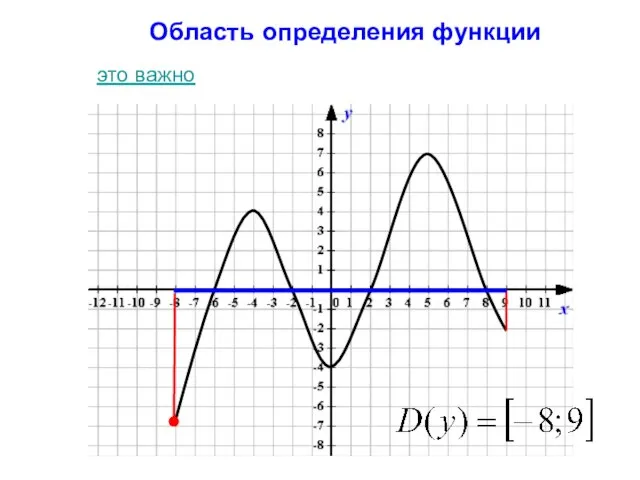
- 3. Область определения функции это важно
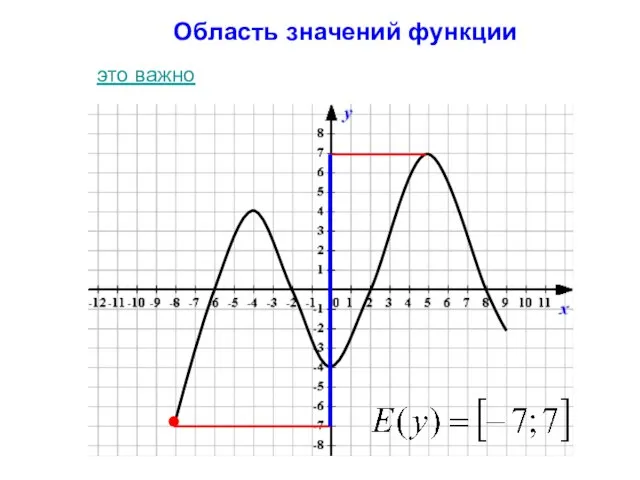
- 4. Область значений функции это важно
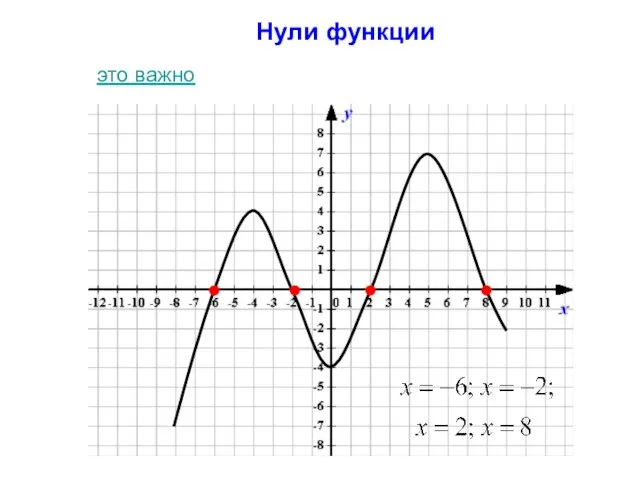
- 5. Нули функции это важно
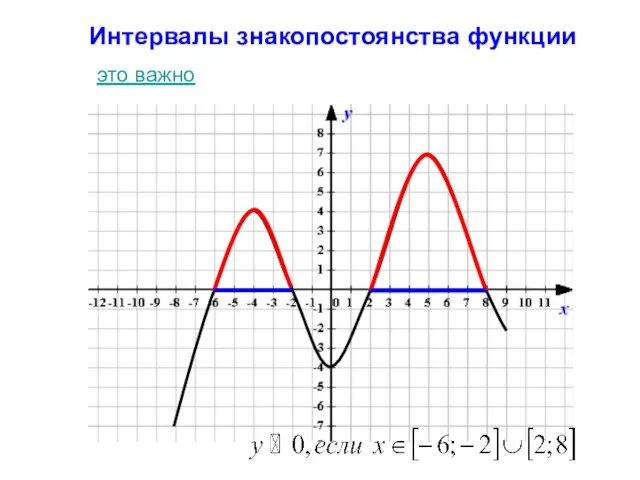
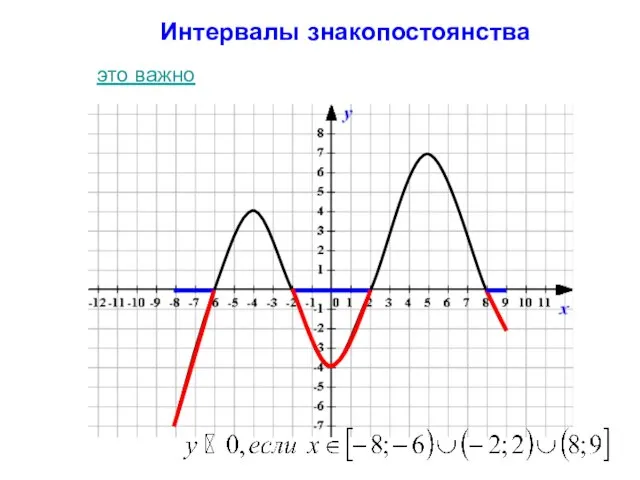
- 6. Интервалы знакопостоянства функции это важно
- 7. Интервалы знакопостоянства это важно
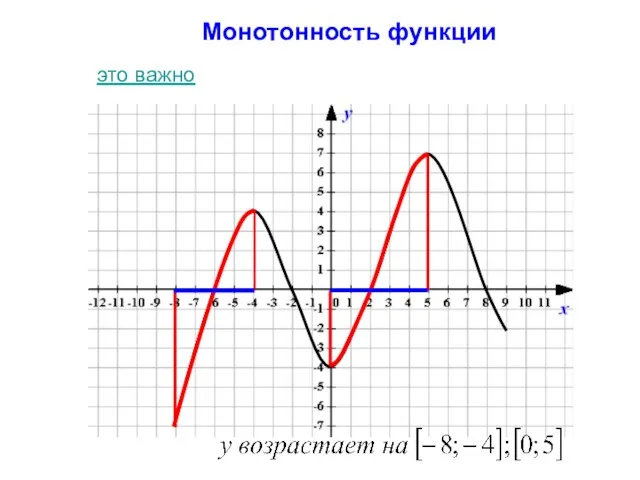
- 8. Монотонность функции это важно
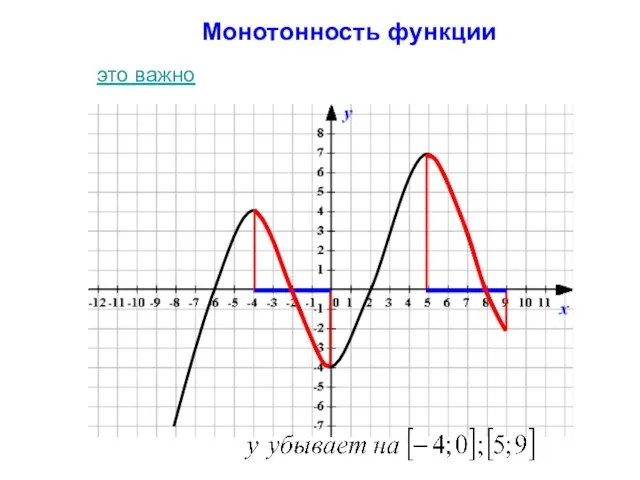
- 9. Монотонность функции это важно
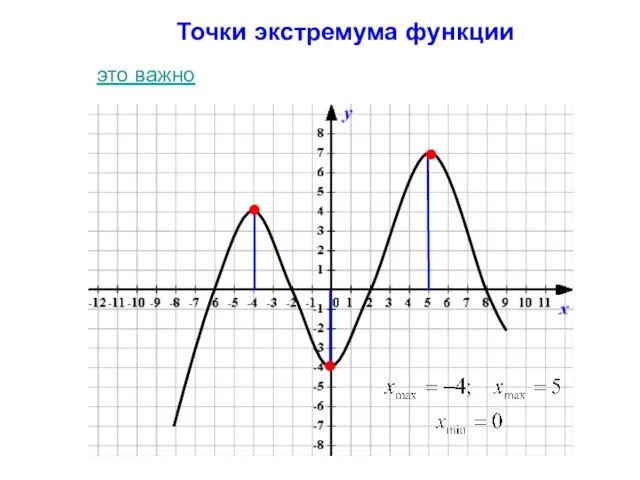
- 10. Точки экстремума функции это важно
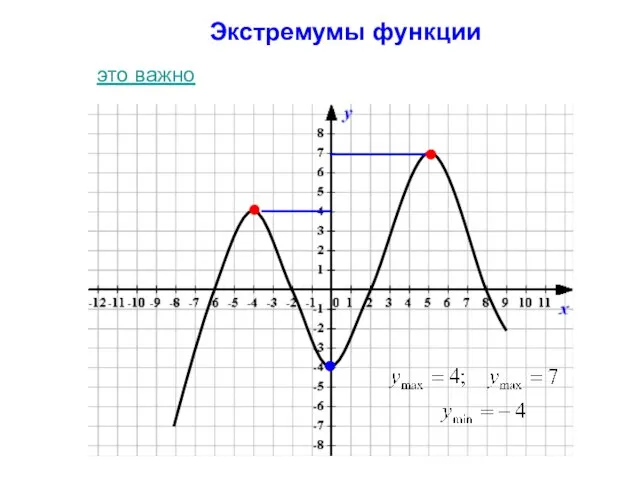
- 11. Экстремумы функции это важно
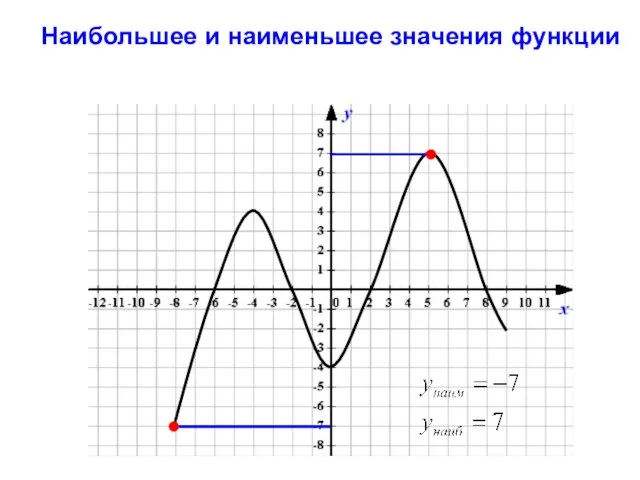
- 12. Наибольшее и наименьшее значения функции
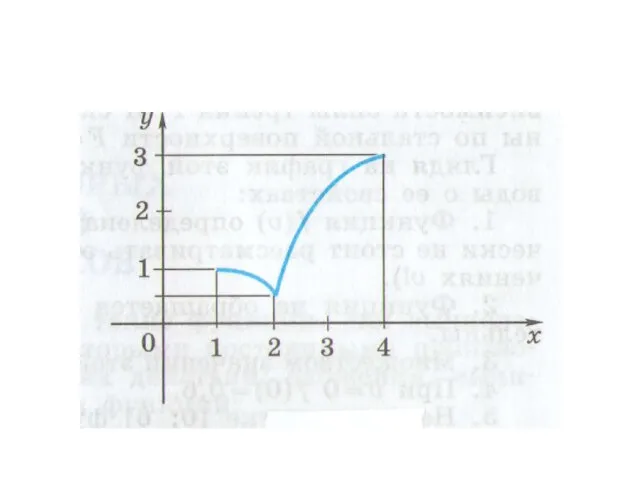
- 17. Область определения функции Все допустимые значения аргумента x функции y(х). назад
- 18. Область значения функции Множество, состоящее из всех чисел y(x), таких, что x принадлежит области определения функции
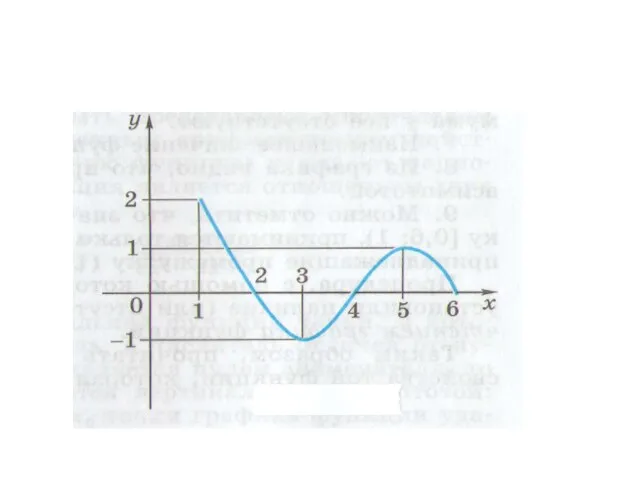
- 19. Нули функции Это значения аргумента х, при которых значение функции у(х) равно нулю. назад
- 20. Интервалы знакопостоянства функции Это промежутки, на которых функция y(х) принимает положительные (отрицательные) значения. назад
- 21. Монотонность функции Функция y(х) убывает на множестве P, если для любых x1 и x2 из множества
- 22. Точки экстремума функции Точка x0 называется точкой минимума функции y(х), если для всех x из некоторой
- 24. Скачать презентацию







 Омск, проспект Губкина, д.1
Омск, проспект Губкина, д.1 Рыжие. Поцелованные солнцем
Рыжие. Поцелованные солнцем Учитель- профессия нужная, важная, самая главная на земле
Учитель- профессия нужная, важная, самая главная на земле Смысловые уровни вещей
Смысловые уровни вещей Презентация на тему "Причины плохого поведения ребенка" - скачать презентации по Педагогике
Презентация на тему "Причины плохого поведения ребенка" - скачать презентации по Педагогике Создание презентаций на ПК
Создание презентаций на ПК Контрольная работа №1 по ЛА и АГ_нов3
Контрольная работа №1 по ЛА и АГ_нов3 aa9c82ab93914bd3847e6c12db9c6ace
aa9c82ab93914bd3847e6c12db9c6ace Задачи в жизненных ситуациях
Задачи в жизненных ситуациях КРУГЛЫЙ СТОЛ «Состояние и перспективы развития профессионального образования в Кабардино-Балкарской Республике с учётом совр
КРУГЛЫЙ СТОЛ «Состояние и перспективы развития профессионального образования в Кабардино-Балкарской Республике с учётом совр Жизнь и творчество
Жизнь и творчество prezentatsia_vkr
prezentatsia_vkr Микросотовая система KIRK 500
Микросотовая система KIRK 500 Реализация личностно-ориентированного обучения в начальной школе
Реализация личностно-ориентированного обучения в начальной школе Использование системно-деятельностнoго подхода на уроках математики
Использование системно-деятельностнoго подхода на уроках математики основная часть урока
основная часть урока Подготовила учитель истории Подготовила учитель истории МОУ Талаканской СОШ №6 Черткова Ольга Александровна
Подготовила учитель истории Подготовила учитель истории МОУ Талаканской СОШ №6 Черткова Ольга Александровна Олимпийский урок
Олимпийский урок Резюме ФИО: Иванова Дарья Абрамовна Дата рождения:10 января, 1927 Место рождения: д. Челкума
Резюме ФИО: Иванова Дарья Абрамовна Дата рождения:10 января, 1927 Место рождения: д. Челкума Управленческая мысль в эпоху Европейского средневековья
Управленческая мысль в эпоху Европейского средневековья Presentation Title
Presentation Title  Аудит бренда. Шаблон
Аудит бренда. Шаблон Обмен веществ и энергии в клетке
Обмен веществ и энергии в клетке  Презентация на тему Типы изомерии
Презентация на тему Типы изомерии Презентация на тему Законы электролиза
Презентация на тему Законы электролиза Презентация на тему Геном человека
Презентация на тему Геном человека Дорогая наша Елена Николаевна!
Дорогая наша Елена Николаевна! МОУ СОШ №4 г.Всеволожска
МОУ СОШ №4 г.Всеволожска