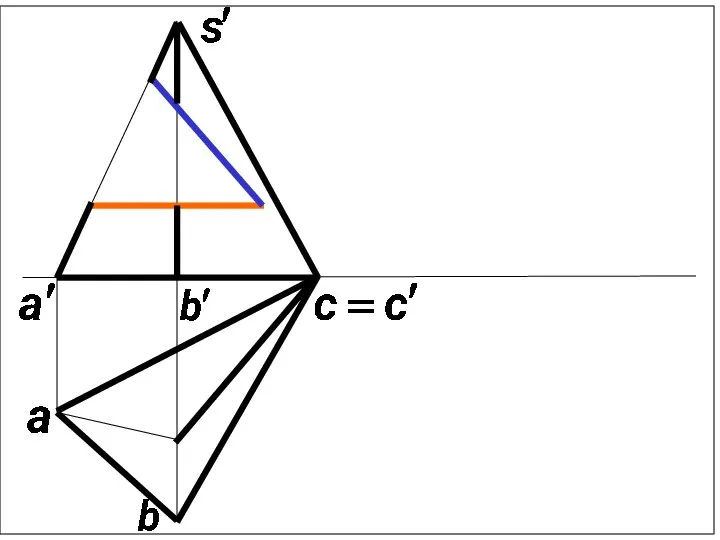
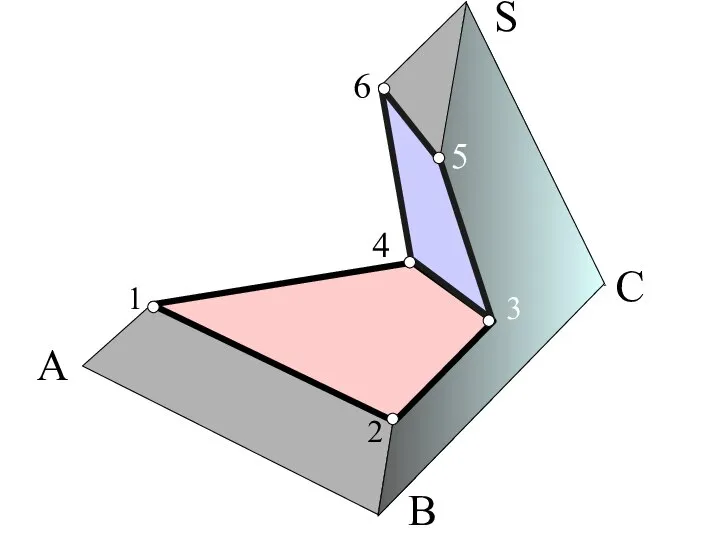
Слайд 2Так как вырез пирамиды призматический
и каждая грань призматического выреза
пересекает пирамиду по плоским
многоугольникам

, то построение этих
многоугольников сводится к задаче на
принадлежность точек поверхности
пирамиды .
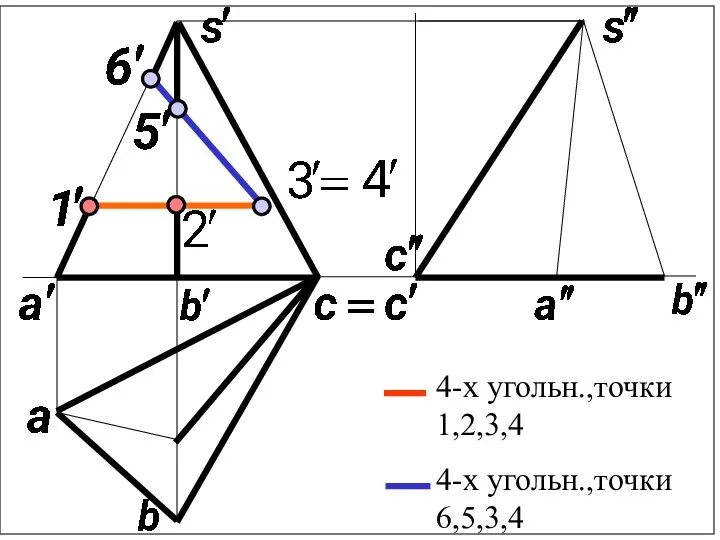
Слайд 4Построим третью проек-
цию пирамиды .
2) Отмечаем точки выреза .
На ребрах пирамиды по
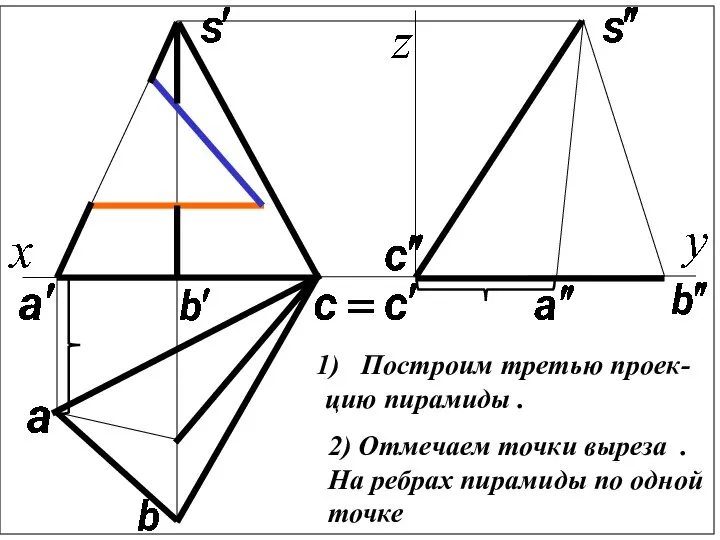
одной
точке
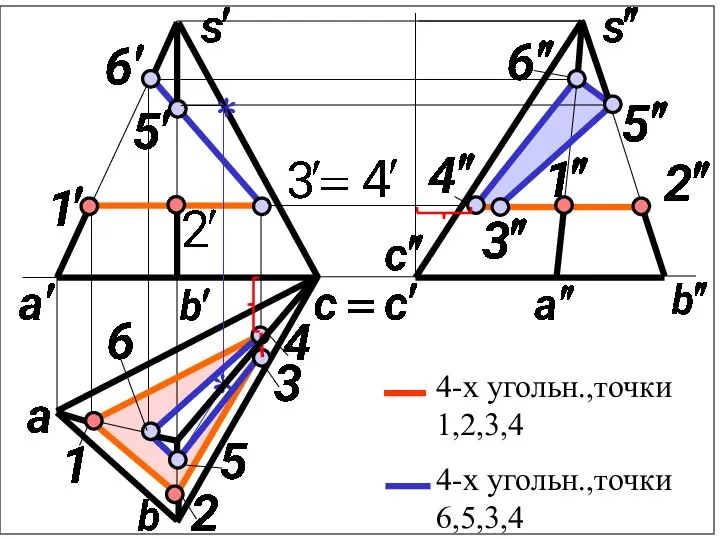
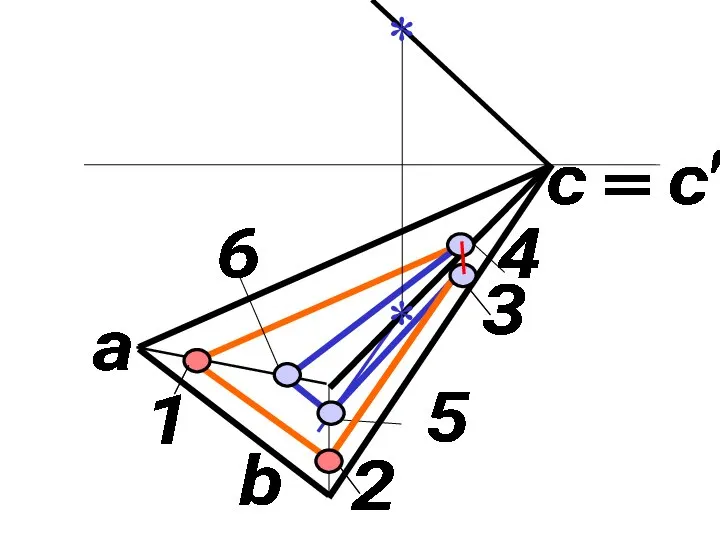
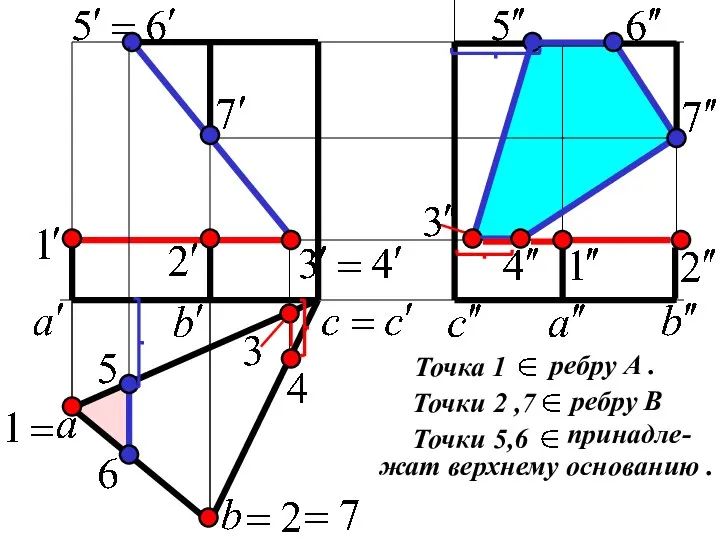
Слайд 63) Точки 1,6 принадлежат ребру SA.
Точки 2,5 принадлежат ребру SB.
Точка 3

принадлежит прямой 2-3 / / BC .
Точка 4 принадлежит прямой 1-4 / /AC .
4) Находим горизонтальные проекции точек,
а затем их профильные проекции
Слайд 10Построить три проекции призмы
с вырезом .

Слайд 11Построим третью проек -
цию .
2) Отмечаем точки выреза.
На ребрах призмы по одной
точке
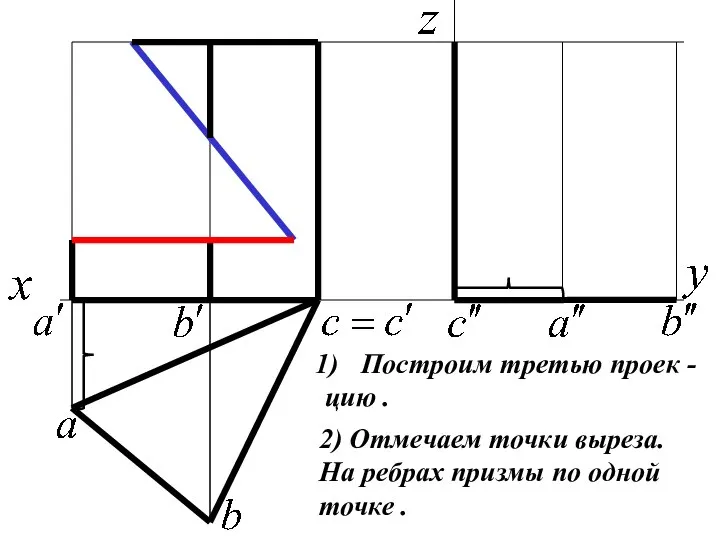
.
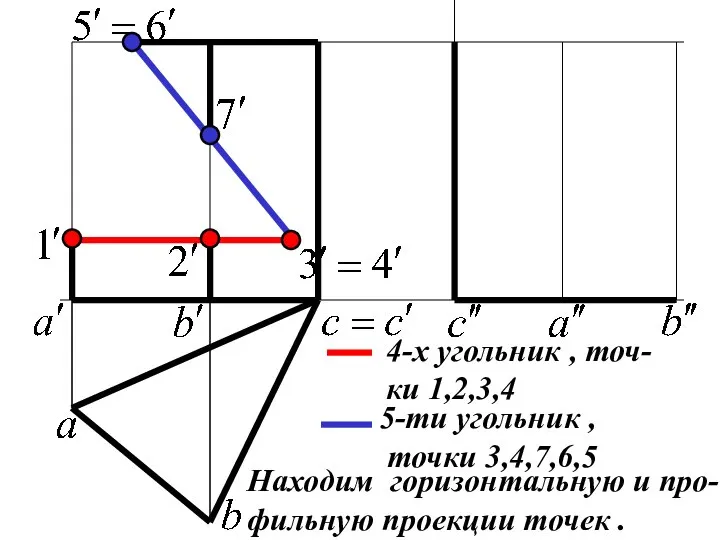
Слайд 12Находим горизонтальную и про-
фильную проекции точек .
Слайд 14Построить три проекции цилиндра с вырезом .

Слайд 15Строим третью проекцию
цилиндра .
2) Отмечаем точки выреза .
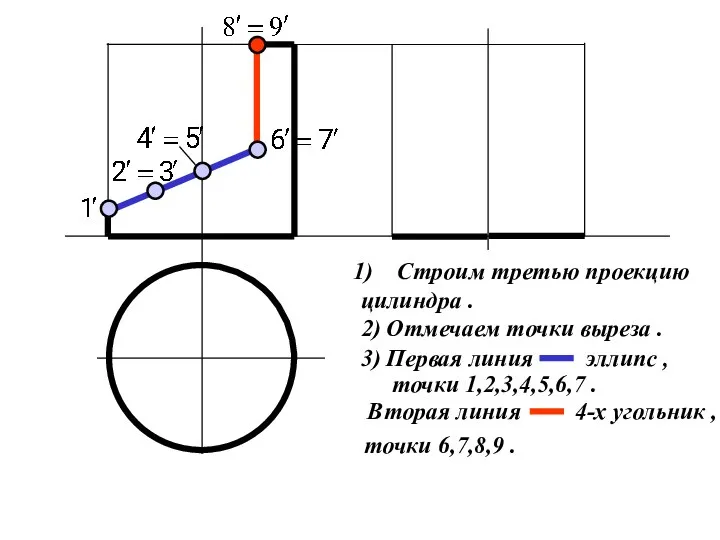
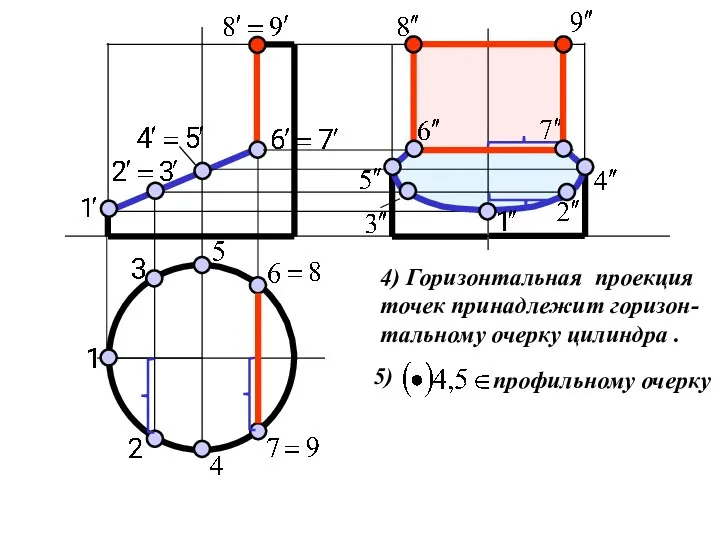
Слайд 164) Горизонтальная проекция
точек принадлежит горизон-
тальному очерку цилиндра .
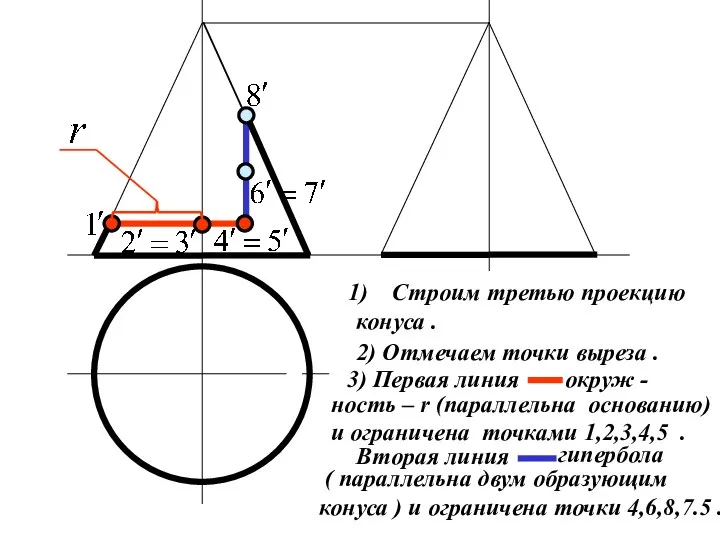
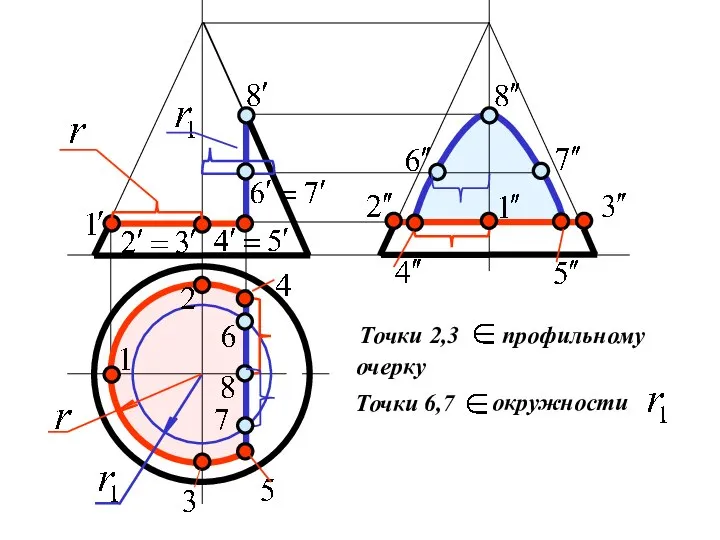
Слайд 17Построить три проекции конуса
с вырезом .

Слайд 18Строим третью проекцию
конуса .
2) Отмечаем точки выреза .
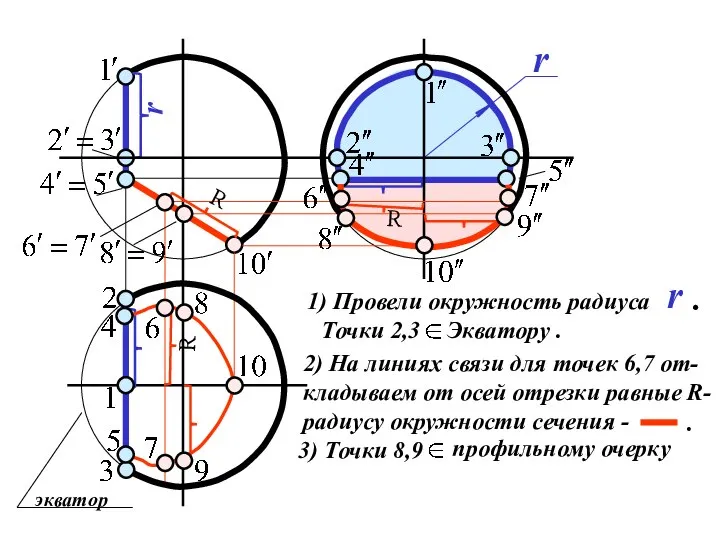
Слайд 20Построить три проекции сферы
с вырезом .

Слайд 211) Построить три проекции сферы .
2) Отмечаем точки выреза сферы ,
на очерке
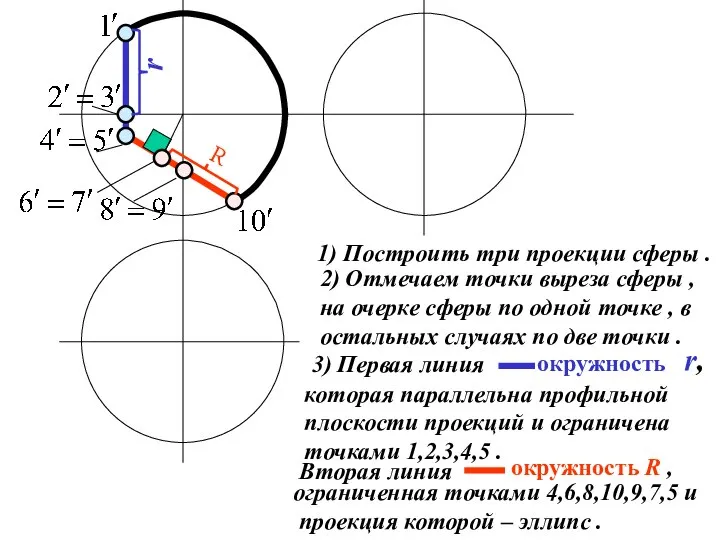
сферы по одной точке , в
остальных случаях по две точки .
Слайд 231) Построить три проекции сферы .
2) Отмечаем точки выреза сферы ,
на очерке
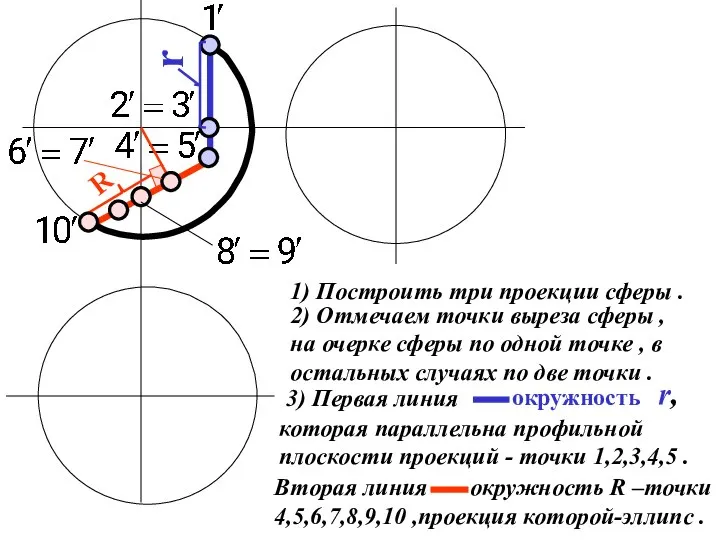
сферы по одной точке , в
остальных случаях по две точки .














 Презентация на тему Роль и значение таможни в современной торговле
Презентация на тему Роль и значение таможни в современной торговле  Человек и источник света
Человек и источник света Современные популярные оздоровительные системы физических упражнений
Современные популярные оздоровительные системы физических упражнений Презентация на тему Межличностные отношения
Презентация на тему Межличностные отношения Интерактивные рисунки – визуальное средство обучения и контроля
Интерактивные рисунки – визуальное средство обучения и контроля Untitled - Made with DesignCap (7)
Untitled - Made with DesignCap (7) Мероприятия и Промоушены
Мероприятия и Промоушены Структура и содержание современного образования Англии
Структура и содержание современного образования Англии Projekt
Projekt Течение
Течение Leadership styles
Leadership styles Истоки развития научной концепции стресса. Стадии развития стресса
Истоки развития научной концепции стресса. Стадии развития стресса Основные направления социальной и образовательной интеграции
Основные направления социальной и образовательной интеграции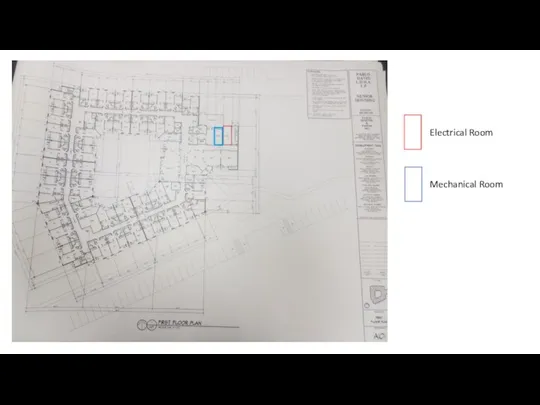 Pablo Equipment Location
Pablo Equipment Location Моя студенческая жизнь!
Моя студенческая жизнь! ЗАИМСТВОВАННЫЕ СЛОВА В РУССКОМ ЯЗЫКЕ
ЗАИМСТВОВАННЫЕ СЛОВА В РУССКОМ ЯЗЫКЕ Physio Radiance - Активируйте ваши клетки кожи
Physio Radiance - Активируйте ваши клетки кожи ВЕРИФИКАЦИЯ ПРОГРАММЫ COSMOS/M ДЛЯ РАСЧЕТА НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ЭЛЕМЕНТОВ И УЗЛОВ ОБОРУДОВАНИЯ И ТРУБОПРОВОДОВ АЭУ
ВЕРИФИКАЦИЯ ПРОГРАММЫ COSMOS/M ДЛЯ РАСЧЕТА НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ЭЛЕМЕНТОВ И УЗЛОВ ОБОРУДОВАНИЯ И ТРУБОПРОВОДОВ АЭУ Научный комплекс России
Научный комплекс России Антикоррупционная политика образовательной организации
Антикоррупционная политика образовательной организации Всероссийская олимпиада школьников 2022-2023
Всероссийская олимпиада школьников 2022-2023 Питание невидимок
Питание невидимок Эвтаназия. Статья 105. Убийство УК РФ
Эвтаназия. Статья 105. Убийство УК РФ Приёмы педагогической техники на уроке иностранного языка
Приёмы педагогической техники на уроке иностранного языка 12.09-16.09
12.09-16.09 МОУ «Деревянкская СОШ №5» Прионежский р-нпоселок Деревянка
МОУ «Деревянкская СОШ №5» Прионежский р-нпоселок Деревянка Презентация на тему Формы работы социального педагога
Презентация на тему Формы работы социального педагога ООО «Охранное предприятие «Масса-Юг»
ООО «Охранное предприятие «Масса-Юг»