Тема:

Решение задач I типа
Решение задач II типа
Решение задач III типа

Решение задачи I типа
Участок леса содержит 96% сосен. Лесозаготовительная компания планирует вырубить на этом участке 150 сосен, в результате чего их содержание понизится до 95%. Сколько сосен останется на участке?

СОСНЫ
x
X - 150
96%
95%
- 150=
СОСНЫ
Блок - схема

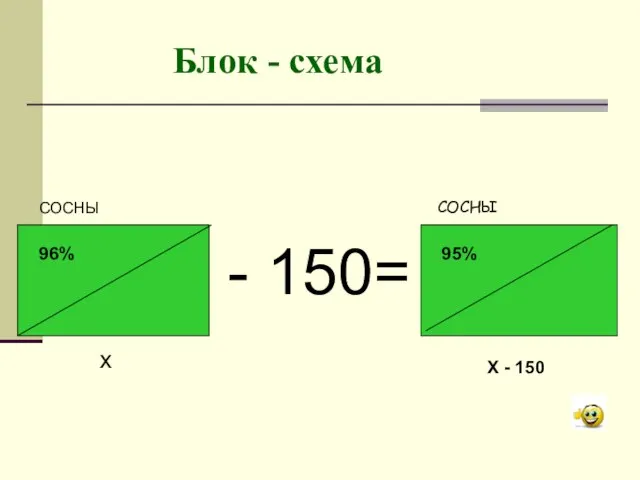
Ход решения задачи
1. 0,96х – 150 = 0,95(х-150)
0,96х – 150 = 0,95х – 0,95∙150
0,96х- 0,95х = 150(1 – 0,95)
0,01х = 150∙0,05 умножим на 100
х = 150∙5
х = 750 (деревьев) было в лесу.
2. 0,95(750-150)=(сосен) стало в лесу.
Ответ: 570 сосен.

Решение задачи II типа
Имеются два слитка сплава золота и меди. Первый слиток содержит 230 г золота и 20 г меди, второй – 240 г золота и 60 г меди. От каждого слитка взяли по куску, сплавили их и получили 300 г сплава, в котором 84% золота. Определите массу (г) куска, взятого от первого слитка?

золото
230(92%)
20г(8%)
250 грамм
240г(80%)
60г(20%)
медь
медь
золото
золото
х
у
84%
16%
медь
300
300 грамм
Блок - схема

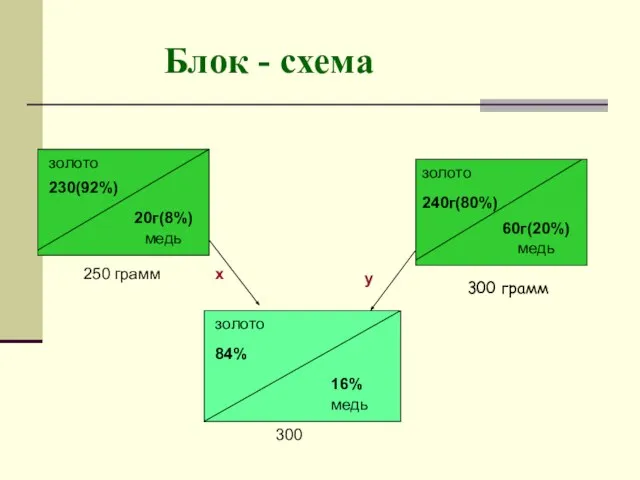
Ход решения задачи
0,6х = 60;
х = 100(г) – масса куска взятого от первого слитка.
Ответ: 100 г.

Формула сложных процентов
С = х (1+а%)n,
где С – новая цена х – первоначальная цена
а - ежемесячная процентная ставка
n – срок вклада (количество месяцев)

Решение задачи III типа
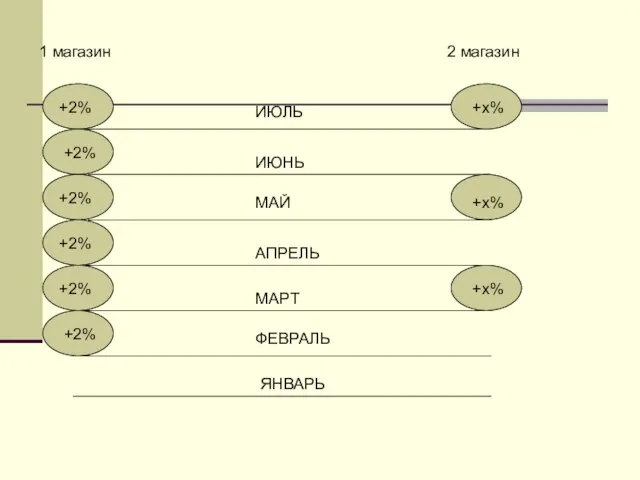
Для определения оптимального режима повышения цен социологи предложили с 1 января повышать цену на один и тот же товар в двух магазинах двумя способами. В одном магазине – в начале каждого месяца (начиная с февраля) на 2 %, в другом – через каждые 2 месяца, в начале третьего (начиная с марта) на одно и тоже число процентов, причем такое, чтобы через полгода (1 июля) цены снова остались одинаковы. Насколько процентов нужно повышать цену товара во втором магазине?

Вопросы:
1. Сколько объектов (фирм, магазинов…) описывается в условии задачи;
2. а) Определить процент повышения (понижения) цен на первом объекте;
б) Сколько месяцев подряд происходило повышение (понижение) цен на первом объекте;
3. а) Определить процент повышения (понижения) цен на втором объекте;
б) Сколько месяцев подряд происходило повышение (понижение) цен на втором объекте;
4. Какое условие задачи является связующим звеном п.2 и п.3;
5. Применить формулу сложных процентов для нахождения цен на обоих объектах.

1 магазин
2 магазин
+2%
+2%
+2%
+2%
+2%
+2%
+x%
+x%
+x%
ИЮЛЬ
ИЮНЬ
МАЙ
АПРЕЛЬ
МАРТ
ФЕВРАЛЬ
ЯНВАРЬ