Тема проекта:

Актуальность:
Актуальность выбранной темы определяется понятием математической компетенции – это способность структурировать данные, вычленять математические отношения, создавать математическую модель ситуации, анализировать и преобразовывать ее, интерпретировать полученные результаты.

Цель:
Разработать не которые методические вопросы по развитию ключевых компетентностей при обучении учащихся 7 – 9 классов решению текстовых задач на составление уравнений

Задачи:
Изучить и кратко изложить некоторые теоретические вопросы компетентностного подхода в обучении.
Применить метод математического моделирования в качестве средства развития ключевых компетентностей.
Разработать конспекты уроков и апробировать разработанные материалы.

В этом мире выживает не самый умный, не самый сильный, не самый красивый, а тот кто умеет приспосабливаться к изменениям.
Ч. Дарвин

Компетентность – это готовность использовать полученные знания и умения в незнакомой жизненной ситуации

Ключевые (базовые) компетентности:
Ценностно-смысловая.
Общекультурная.
Учебно-познавательная.
Информационная.
Коммуникативная.
Социально-трудовая.

Математическая модель – это приближенное описание какого-нибудь класса явлений, выраженное на языке какой-нибудь математической теории.

Этапы математического моделирования:
Построение математической модели.
Исследование полученной модели.
Интерпретация полученного результата с точки зрения исходной ситуации.

Обучение математическому моделированию при решении задач «на движение»

Решение развернутым текстом
Решите задачу, заполняя пропуски:
От пристани А отошел теплоход со скоростью 45 км/ч . Через 45 мин от пристани В навстречу ему отошел второй теплоход, скорость которого 36 км/ч. Через сколько часов после отправления первого теплохода они встретятся , если расстояние между пристанями А и В равно 162 км ?
Решение.
Пусть x (ч) - время до встречи первого теплохода, тогда ( x -..….)(ч) - время до встречи второго теплохода.
Находим: ( 45…….)(км) – расстояние, пройденное первым теплоходом до встречи, ( х - …..)……..(км) - расстояние, пройденное вторым теплоходом до встречи. По условию задачи известно, что расстояние между пристанями равно ………., поэтому составляем уравнение: 45…..+ ( х - .…..)….…..=……..
Решаем уравнение: …………………………………………………………………………………………
Итак, через …….. часа после отправления первого теплохода они встретились.
Ответ:…час.

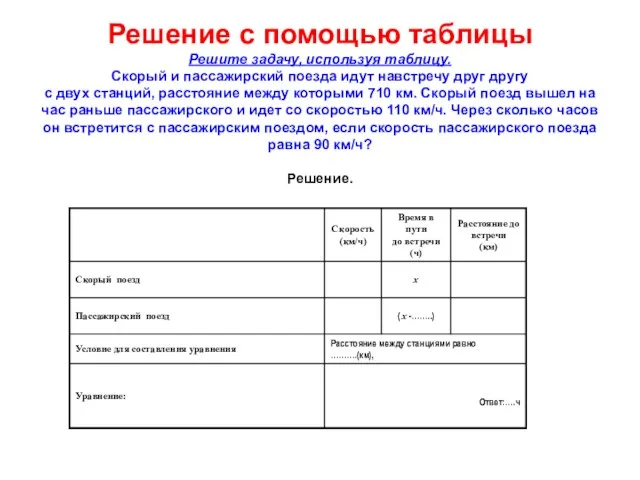
Решение с помощью таблицы
Решите задачу, используя таблицу.
Скорый и пассажирский поезда идут навстречу друг другу
с двух станций, расстояние между которыми 710 км. Скорый поезд вышел на час раньше пассажирского и идет со скоростью 110 км/ч. Через сколько часов он встретится с пассажирским поездом, если скорость пассажирского поезда равна 90 км/ч?
Решение.

Тестирование – один из эффективных способов контроля за усвоением полученных знаний.
Виды заданий в тестах:
1.Выберите уравнение, которое соответствует условию задачи.
2.Выберите модель, соответствующую условию задачи.
3.Решите задачу (с выбором правильного ответа).

Решение задач
«на движение»
Алгебра 9 класс

Задачи на движение обычно содержат следующие величины:
– время,
– скорость, – расстояние.
Уравнения, связывающее эти три величины:
v
S
t

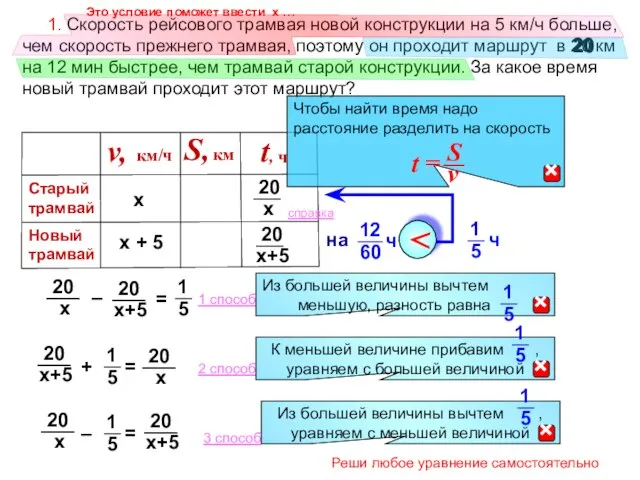
1. Скорость рейсового трамвая новой конструкции на 5 км/ч больше, чем скорость прежнего трамвая, поэтому он проходит маршрут в 20 км на 12 мин быстрее, чем трамвай старой конструкции. За какое время новый трамвай проходит этот маршрут?
х + 5
20
20
справка
Это условие поможет ввести х …
1 способ
2 способ
3 способ
Реши любое уравнение самостоятельно

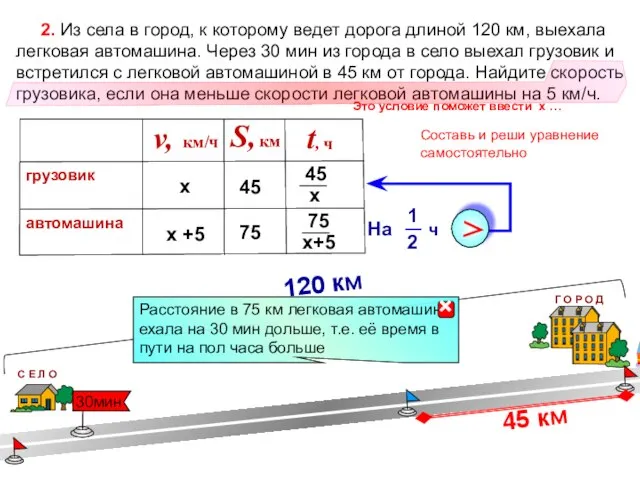
2. Из села в город, к которому ведет дорога длиной 120 км, выехала легковая автомашина. Через 30 мин из города в село выехал грузовик и встретился с легковой автомашиной в 45 км от города. Найдите скорость грузовика, если она меньше скорости легковой автомашины на 5 км/ч.
С Е Л О
х +5
45
75
Это условие поможет ввести х …
Составь и реши уравнение самостоятельно

Задачи для самостоятельной работы.
1.
Некоторую часть дня автобус работает в режиме экспресса. При этом его рейсовая скорость увеличивается на 8 км/ч, а время, затраченное на маршрут в 16 км, сокращается на 4 мин. За какое время проходит этот маршрут автобус в режиме экспресса?
2.
За 70 км до конечной станции поезд опаздывал на 10 мин. Чтобы прийти в пункт назначения вовремя, машинист увеличил скорость на 10 км/ч. С какой скоростью шел поезд последние 70 км?
3.
Турист отправился на автомашине из города А в город В. Первые 75 км он ехал со скоростью на 10 км/ч меньшей, чем рассчитывал, а остальной путь со скоростью, на 10 км/ч большей, чем рассчитывал. В город В, который удалён на 180 км, турист прибыл вовремя. С какой скоростью он ехал в конце пути?

Задача 1.
Задача 2.
Задача 3.
Задачи для самостоятельной работы
мин
км/ч
км/ч

Работа по моделированию текстовых задач на уроках алгебры имеет практическую значимость для повышения качества образовательного процесса