Тема: Решение неравенств второй степени с одной переменной.

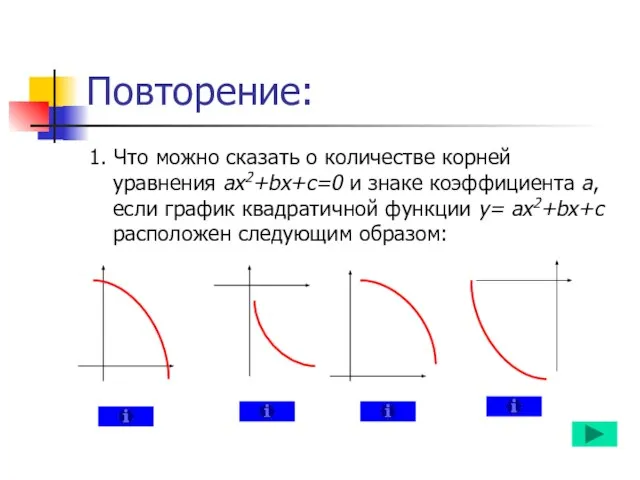
Повторение:
1. Что можно сказать о количестве корней уравнения ах2+bx+c=0 и знаке коэффициента а, если график квадратичной функции у= ах2+bx+c расположен следующим образом:

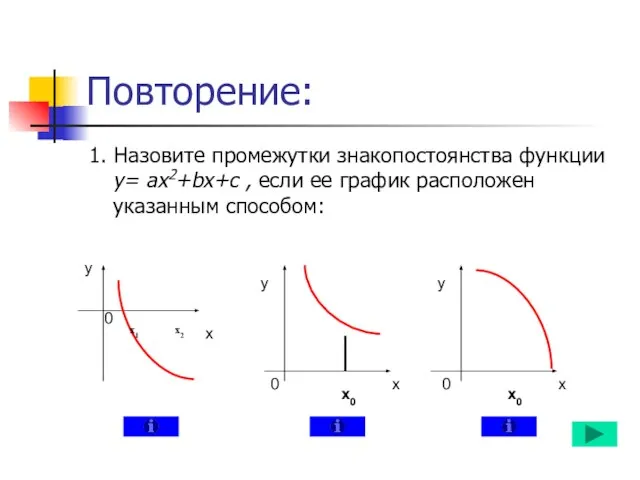
Повторение:
1. Назовите промежутки знакопостоянства функции у= ах2+bx+c , если ее график расположен указанным способом:
х1
х0
х0
х2
0
0
0
у
у
у
х
х
х

Два корня!
а>0

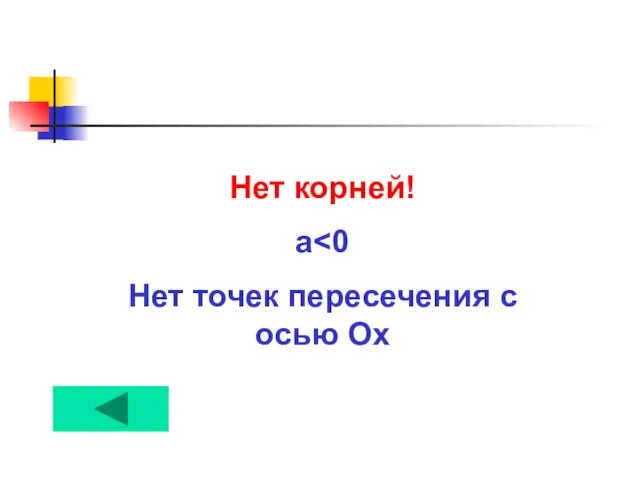
Нет корней!
a<0
Нет точек пересечения с осью Ох

Нет корней!
а>0
Нет точек пересечения с осью Ох

Один корень!
a<0
Одна точка пересечения с осью Ох.

при
при

при

при

Определение:
Неравенства ах 2 +bx+c>0,
ах2 +bx+c<0, где х – независимая переменная, a, b и c – некоторые числа, причем а≠0, называют неравенствами второй степени с одной переменной.

Решение неравенств второй степени с одной переменной можно рассматривать как нахождение промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения.

Пример 1.
Решим неравенство 5х2+9х-2<0.
Рассмотрим функцию у= 5х2+9х-2.
График ее парабола, ветви
направлены вверх. Выясним, в каких точках парабола пересекает ось Ох.
5х2+9х-2=0
Х1= -2; х2=1/5.

Пример 1
Покажем схематически, как
расположена парабола в
координатной плоскости.
-2
1/5
Функция принимает только отрицательные значения, когда
Следовательно:
Множеством решений данного неравенства является числовой
промежуток

Алгоритм решения неравенств второй степени:
Находят дискриминант квадратного трехчлена и выясняют, имеет ли трехчлен корни;

Алгоритм решения неравенств второй степени:
Если трехчлен имеет корни, то отмечают их на оси х и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх при а>0 или вниз при а<0;

Алгоритм решения неравенств второй степени:
если трехчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при а>0 или в нижней при а<0;

Алгоритм решения неравенств второй степени:
Находят на оси х промежутки, для которых точки параболы расположены выше оси х (если решают неравенство ах2+bx+c>0) или ниже оси х (если решают неравенство ах2+bx+c<0).