Теорема Пифагора

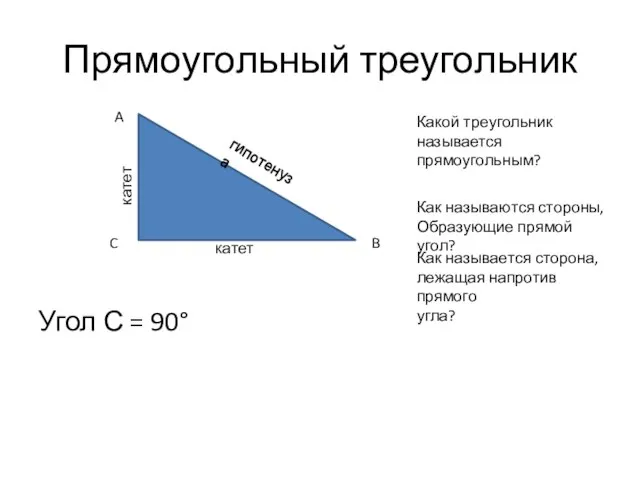
Прямоугольный треугольник
Угол С = 90°
A
C
B
катет
катет
гипотенуза
Какой треугольник называется прямоугольным?
Как называются стороны,
Образующие прямой угол?
Как называется сторона,
лежащая напротив прямого
угла?

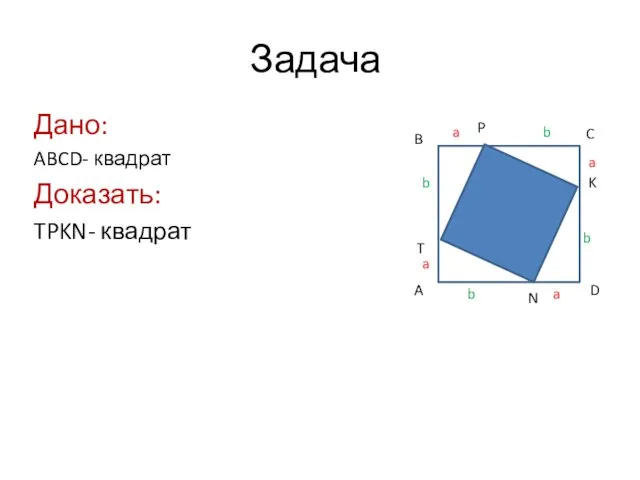
Задача
Дано:
ABCD- квадрат
Доказать:
TPKN- квадрат
A
B
C
D
T
P
K
N
a
a
a
a
b
b
b
b

Немного истории…
Пифагор Самосский ( 570—490 гг. до н. э.) — древнегреческий философ и математик, создатель религиозно-философской школы пифагорейцев.
Историю жизни Пифагора трудно отделить от легенд, представляющих его в качестве совершенного мудреца и великого посвящённого во все таинства греков и варваров. Ещё Геродот называл его «величайшим эллинским мудрецом».

Школа была основана Пифагором в Кротоне (Южная Италия) и просуществовала до начала IV в. до н.э., хотя гонения на нее начались практически сразу после смерти Пифагора в 500 г. По сути, это была первая философская школа, религиозно-философское аристократическое братство; она имела большое влияние на греческие полисы Южной Италии и Сицилии.
Союз отличался строгими обычаями и высокой нравственностью. Образ жизни пифагорейцев вошел в историю: как рассказывают легенды, учеников Школы всегда можно было узнать по их внешнему облику и благородному поведению.
Пифагорейская школа положила начало математическим наукам. В пифагорейской школе начали развиваться астрономия и медицина.

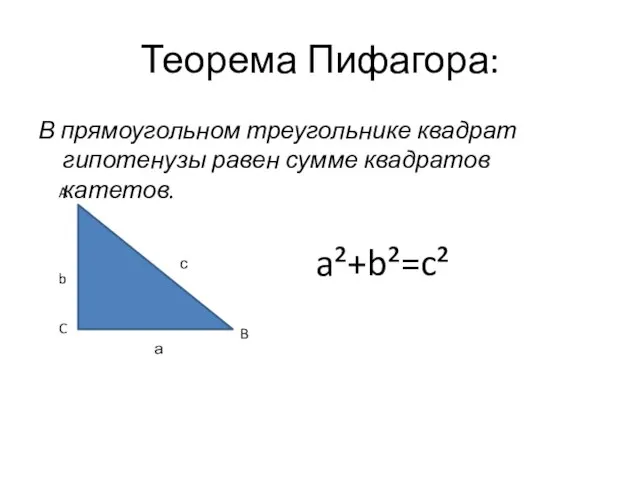
Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
A
B
C
b
с
а
a²+b²=c²

Доказательство
Достроим треугольник до квадрата со стороной a+b. Его площадь равна S=(a+b)²[1]
С другой стороны этот квадрат состоит из четырех равных треугольников
Sтр=1/2ab; 4Sтр=2ab
и квадрата со стороной с
Sкв=с²
Отсюда S=2ab+c² [2]
a
b
c
a
b
c
c
c
a
a
b
b

Из [1] и [2] получим
(a+b)²=2ab+c²
a²+ b²+2ab=2ab+c²
a²+b²=c²
Что и требовалось доказать.

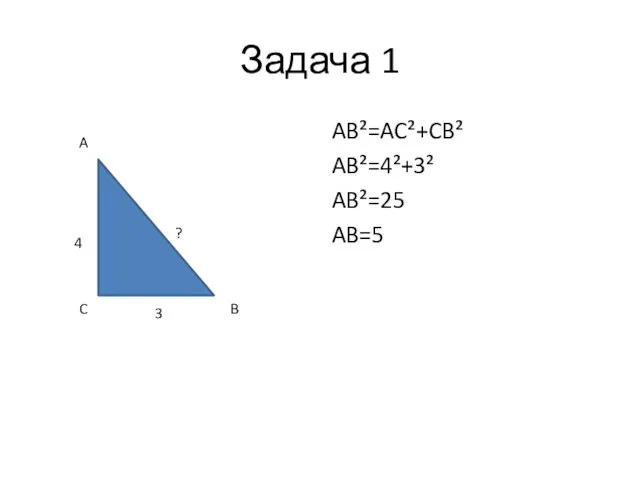
Задача 1
AB²=AC²+CB²
AB²=4²+3²
AB²=25
AB=5
4
3
?
A
C
B

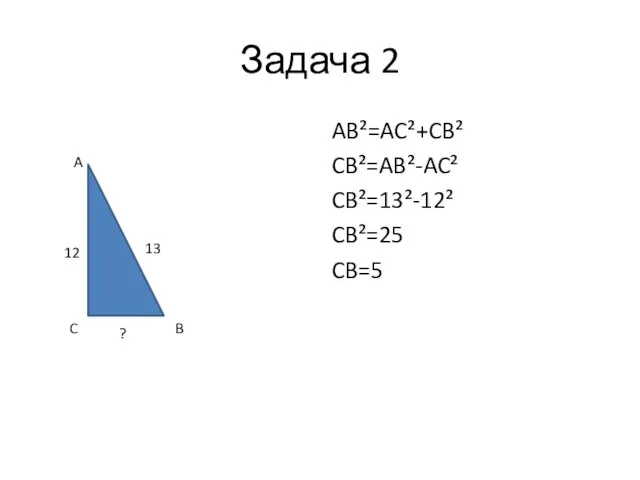
Задача 2
AB²=AC²+CB²
CB²=AB²-AC²
CB²=13²-12²
CB²=25
CB=5
A
C
B
13
12
?

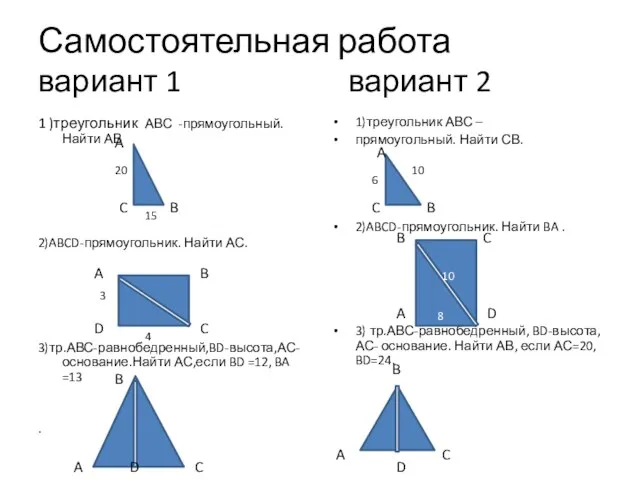
Самостоятельная работа
вариант 1 вариант 2
1 )треугольник АВС -прямоугольный. Найти АВ
2)ABCD-прямоугольник. Найти АС.
3)тр.АВС-равнобедренный,BD-высота,АС-основание.Найти АС,если BD =12, BA =13
.
1)треугольник АВС –
прямоугольный. Найти СВ.
2)ABCD-прямоугольник. Найти BA .
3) тр.АВС-равнобедренный, BD-высота, АС- основание. Найти АВ, если АС=20, BD=24.
C
A
B
A
D
B
C
A
B
C
D
C
A
B
A
B
C
D
A
B
C
D
20
15
4
3
6
10
10
8

Решение:
Вариант 1.
1)AB²=AC²+CB²
AB²=20²+15²
AB²=625
AB=25
2)ACD-прямоуг.
AC²=AD²+DC²
AC²=4²+3²
AC²=25
AC=5
3)ABD прямоуг.
AD²=AB²-BD²
AD²=13²-12²
AD²=25
AD=5
AC=2AD=2*5=10
Вариант 2
1)AB²=AC²+CB²
BC²=AB²-AC²
BC²=10²-6²
BC²=64
BC=8
2) BAD- прямоуг.
BA²=BD²-AD²
BA²=10²-8²
BA²=36
BA=6
3)AD=½AC=10
ABD прямоуг.
AB²=AD²+BD²
AB²=10²+24²
AB²=676
AB=26

Итог урока:
Сформулируйте теорему Пифагора,
Как найти катет прямоугольного треугольника, зная гипотенузу и другой катет.

Домашнее задание:
П. 54-читать,
с.129 вопрос №8,
№486