Содержание
- 2. Выполните устно упражнения Раскройте скобки Вычислите при х = 1, 2, 3, 4 Найдите площадь квадрата
- 3. Вопрос - ответ Угол, градусная мера которого равна 90° ПРЯМОЙ Сторона, лежащая напротив прямого угла треугольника
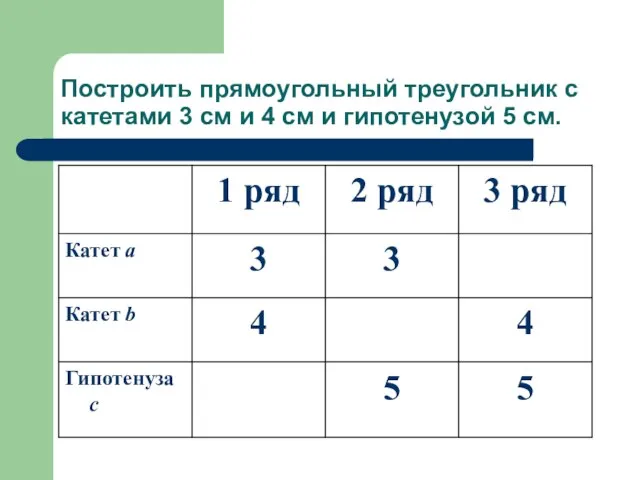
- 4. Построить прямоугольный треугольник с катетами 3 см и 4 см и гипотенузой 5 см.
- 5. Пифагор Самосский (ок. 580 – ок. 500 до н.э.) Древнегреческий математик и философ. Родился на острове
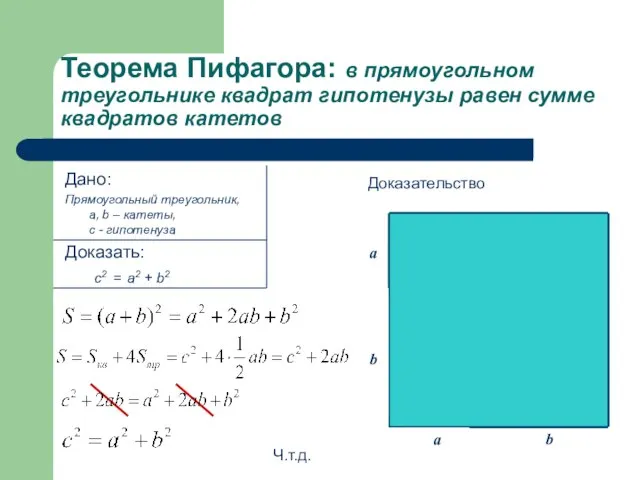
- 6. Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов Дано: Прямоугольный треугольник, a, b
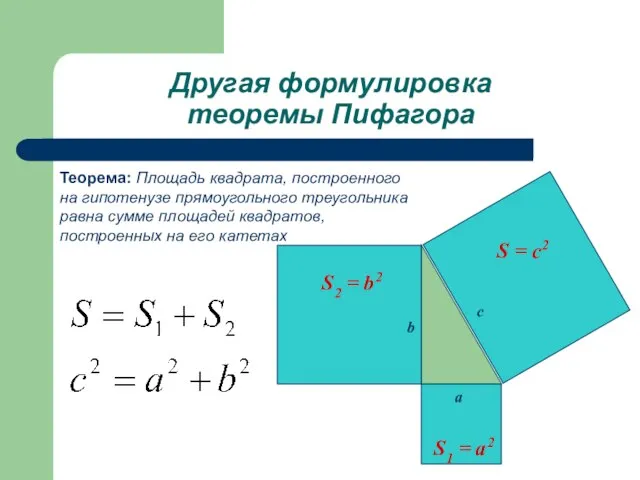
- 7. Другая формулировка теоремы Пифагора S = c2 S2 = b2 S1 = a2 a b c
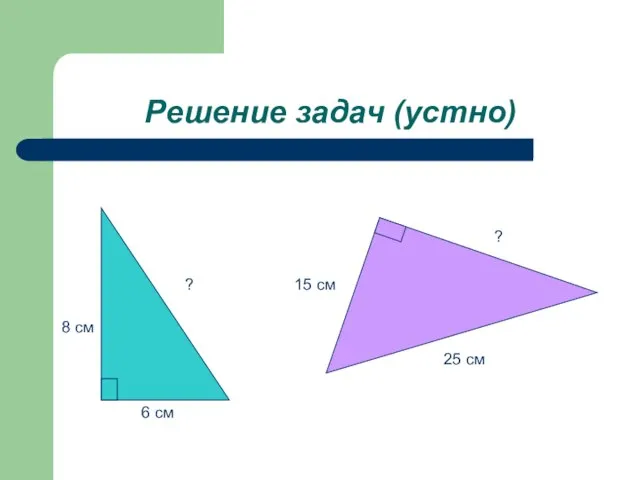
- 8. Решение задач (устно) 6 см 8 см ? 15 см ? 25 см
- 9. Решение задач (в тетради) Дано: a, b – катеты прямоугольного треугольника, с – гипотенуза a =
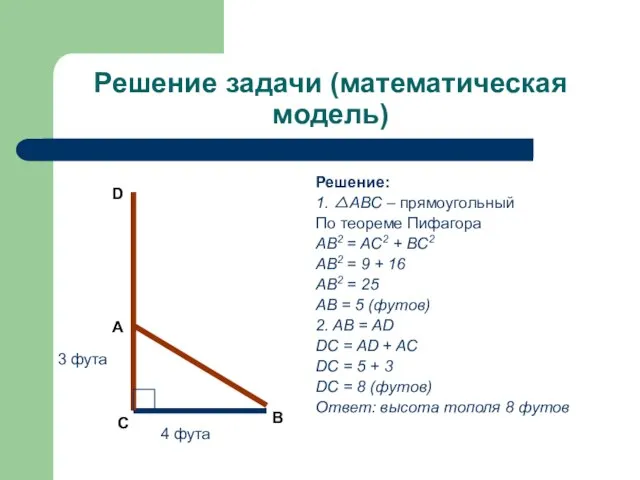
- 10. Задача индийского математика XII века Бхаскары На берегу реки рос тополь одинокий. Вдруг ветра порыв его
- 11. Решение задачи (математическая модель) Решение: 1. △ABC – прямоугольный По теореме Пифагора AB2 = AC2 +
- 13. Скачать презентацию





 Изображения изделий и их обозначения при выполнении графических конструкторских документов
Изображения изделий и их обозначения при выполнении графических конструкторских документов Использование функций
Использование функций Математические задачи от русских, советских и зарубежных писателей
Математические задачи от русских, советских и зарубежных писателей Каникулы в международном детском лагере
Каникулы в международном детском лагере Язык есть исповедь народа
Язык есть исповедь народа Работа по стимулированию юридических лиц и индивидуальных предпринимателей к трудоустройству безработных
Работа по стимулированию юридических лиц и индивидуальных предпринимателей к трудоустройству безработных Физико-географическое районирование Северной Евразии
Физико-географическое районирование Северной Евразии  Узоры “тетёрки ” на печенье
Узоры “тетёрки ” на печенье Презентация на тему Постоянные магниты
Презентация на тему Постоянные магниты Весенний фестиваль для учащихся
Весенний фестиваль для учащихся 23 февраля. Поздравляем!
23 февраля. Поздравляем! Российский государственный университет нефти и газа имени И.М.Губкина Кафедра машин и оборудования нефтяной и газовой промышленн
Российский государственный университет нефти и газа имени И.М.Губкина Кафедра машин и оборудования нефтяной и газовой промышленн Звук и свет в лирике И. Анненского
Звук и свет в лирике И. Анненского Книжка-раскраска
Книжка-раскраска Взаимодействие научного руководителя со студентами через личный кабинет с использование сервиса Антиплагиат
Взаимодействие научного руководителя со студентами через личный кабинет с использование сервиса Антиплагиат Зачем живые организмы запасают питательные вещества?
Зачем живые организмы запасают питательные вещества? Особенности приема 2020 (колледж). Дистанционная подача документов
Особенности приема 2020 (колледж). Дистанционная подача документов Ресурсный Центр «Кристина»
Ресурсный Центр «Кристина» Проверка правильности кирпичной кладки
Проверка правильности кирпичной кладки Смешанное обучение – blended learning
Смешанное обучение – blended learning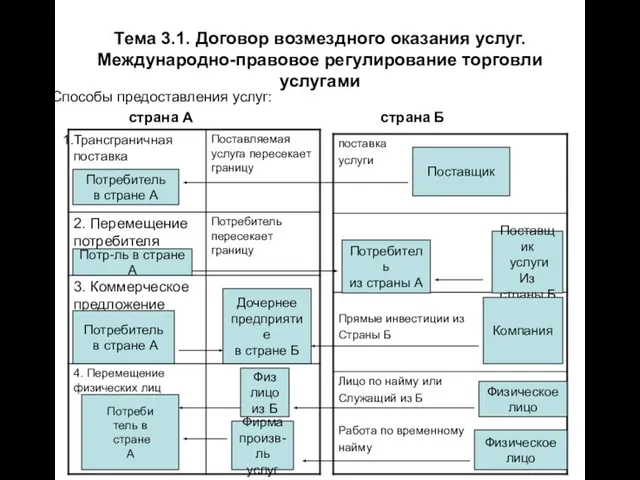 Тема 3.1. Договор возмездного оказания услуг. Международно-правовое регулирование торговли услугами Способы предоставления услуг
Тема 3.1. Договор возмездного оказания услуг. Международно-правовое регулирование торговли услугами Способы предоставления услуг Конвенция о правах ребенка
Конвенция о правах ребенка Богомолова Роза Александровна
Богомолова Роза Александровна Renault Assistance. Служба маркетинга запасных частей и послепродажного обслуживания
Renault Assistance. Служба маркетинга запасных частей и послепродажного обслуживания Принцип действия жидкокристаллических дисплеев
Принцип действия жидкокристаллических дисплеев Правила работы с обучающей презентацией
Правила работы с обучающей презентацией плакат
плакат ОП по Гагинскому району МО МВД России Большеболдинский: история, сегодняшнее состояние и перспективы развития
ОП по Гагинскому району МО МВД России Большеболдинский: история, сегодняшнее состояние и перспективы развития