Теорема Пифагора

Формулировки теоремы
Геометрическая
Алгебраическая

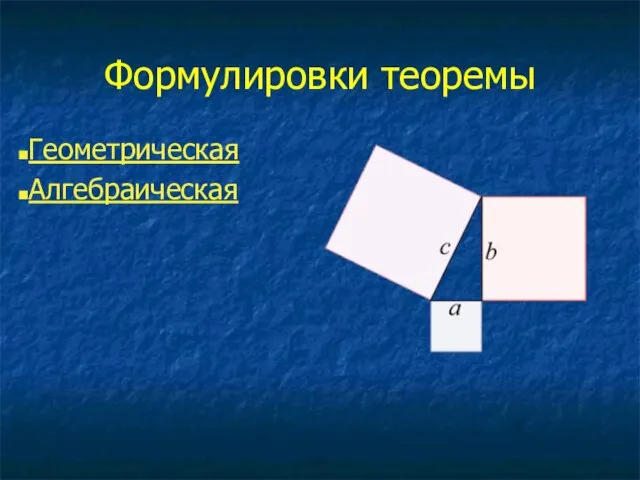
Геометрическая
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Алгебраическая
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:

Доказательства
В научной литературе зафиксировано 367 доказательств данной теоремы.
Теорема Пифагора является единственной теоремой со столь внушительным числом доказательств.
Способы доказательства теоремы:
Через подобные треугольники.
Доказательство методом площадей.
Доказательство через равнодополняемость.
Доказательство через равносоставленность.
Доказательство Евклида.